All Pair Shortest Path IOIACM ICPC Training June

All Pair Shortest Path IOI/ACM ICPC Training June 2004

All Pair Shortest Path n Note: Dijkstra’s Algorithm takes O((V+E)log. V) time n n All Pair Shortest Path Problem can be solved by executing Dijkstra’s Algorithm |V| times Running Time: O(V(V+E)log V) n Floyd-Warshall Algorithm: O(V 3)

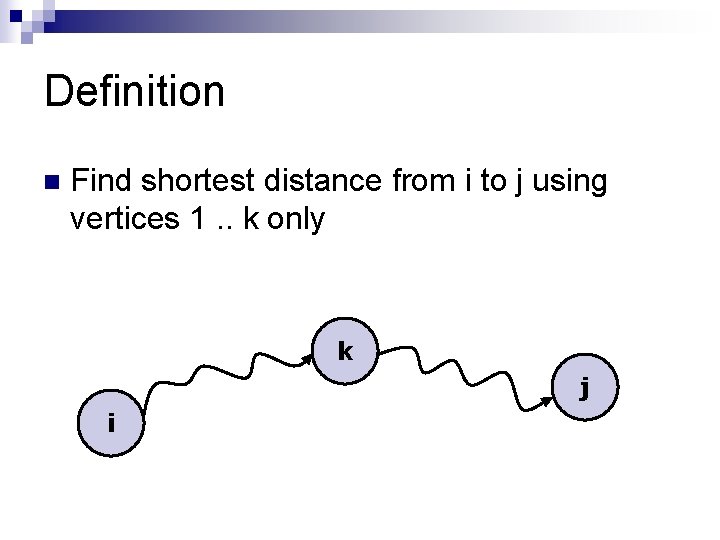
Idea n Label the vertices with integers 1. . n n Restrict the shortest paths from i to j to consist of vertices 1. . k only (except i and j) Iteratively relax k from 1 to n. n k j i

Definition n Find shortest distance from i to j using vertices 1. . k only k j i

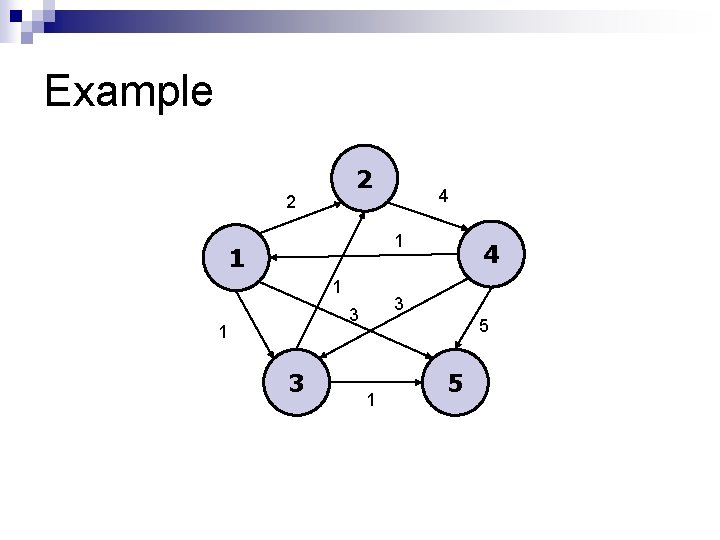
Example 2 2 4 1 1 1 3 3 1 3 4 5 1 5

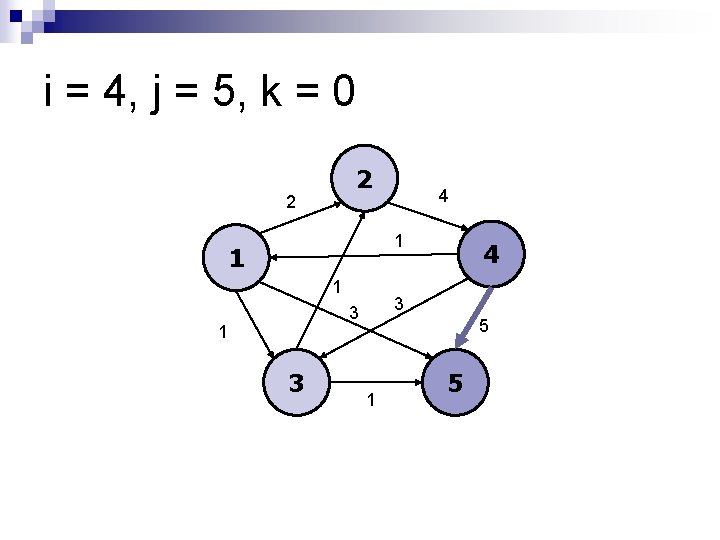
i = 4, j = 5, k = 0 2 2 4 1 1 1 3 3 1 3 4 5 1 5

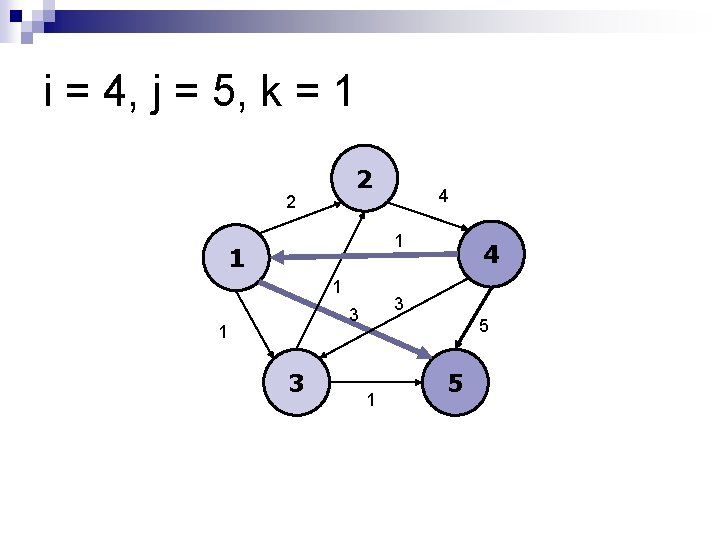
i = 4, j = 5, k = 1 2 2 4 1 1 1 3 3 1 3 4 5 1 5

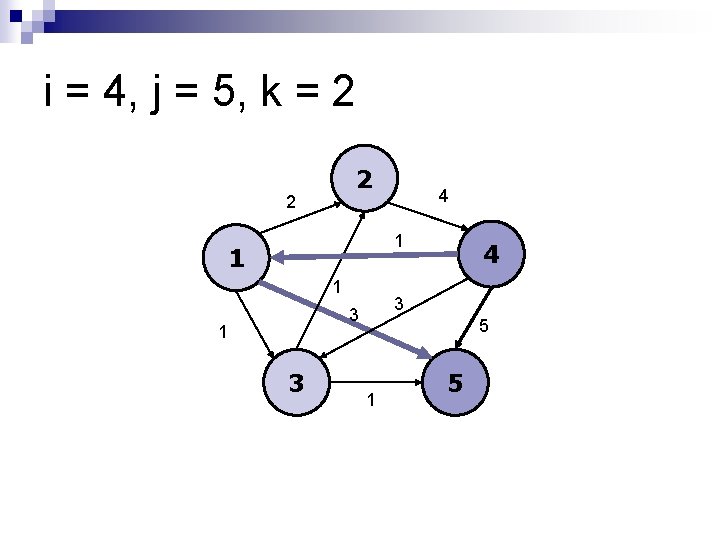
i = 4, j = 5, k = 2 2 2 4 1 1 1 3 3 1 3 4 5 1 5

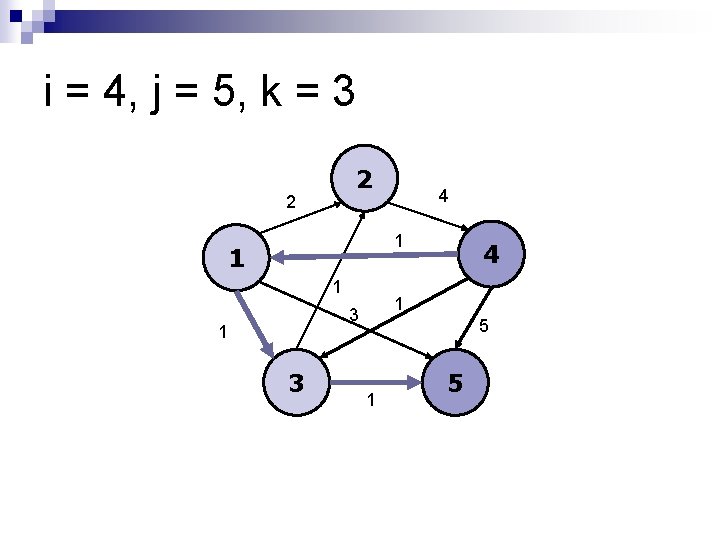
i = 4, j = 5, k = 3 2 2 4 1 1 3 1 3 4 5 1 5

Idea k j i

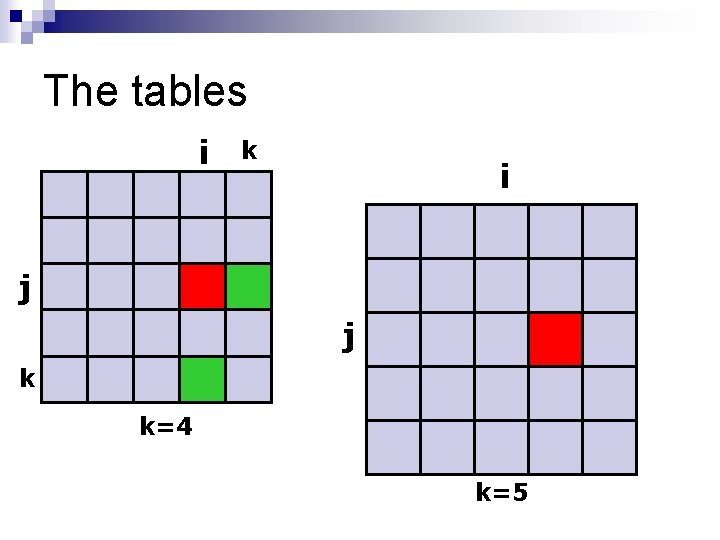
The tables i k i j j k k=4 k=5

The code for i = 1 to |V| for j = 1 to |V| a[i][j][0] = cost(i, j) for k = 1 to |V| for i = 1 to |V| for j = 1 to |V| a[i][j][k] = min( a[i][j][k-1], a[i][k][k-1] + a[k][j][k-1])

Topological sort IOI/ACM ICPC Training June 2004

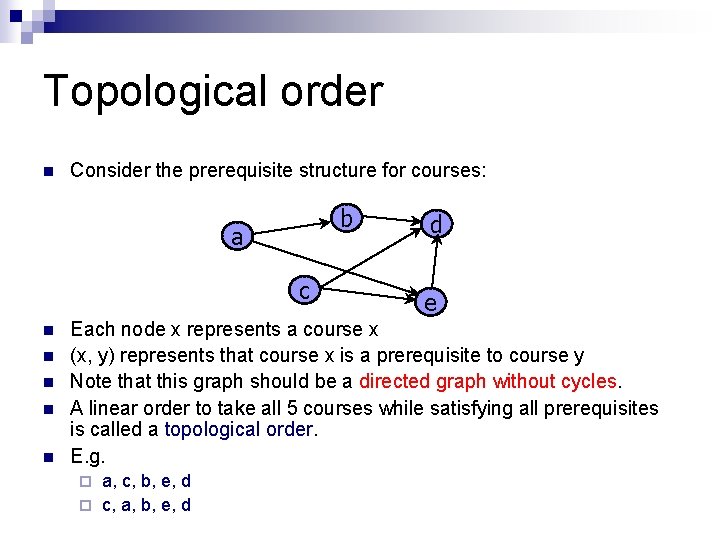
Topological order n Consider the prerequisite structure for courses: b a c n n n d e Each node x represents a course x (x, y) represents that course x is a prerequisite to course y Note that this graph should be a directed graph without cycles. A linear order to take all 5 courses while satisfying all prerequisites is called a topological order. E. g. a, c, b, e, d ¨ c, a, b, e, d ¨

Topological sort n Arranging all nodes in the graph in a topological order n Applications: ¨ Schedule tasks associated with a project

Topological sort algorithm Algorithm top. Sort 1 n = |V|; Let R[0. . n-1] be the result array; for i = 1 to n { select a node v that has no successor; R[n-i] = v; delete node v and its edges from the graph; } return R;

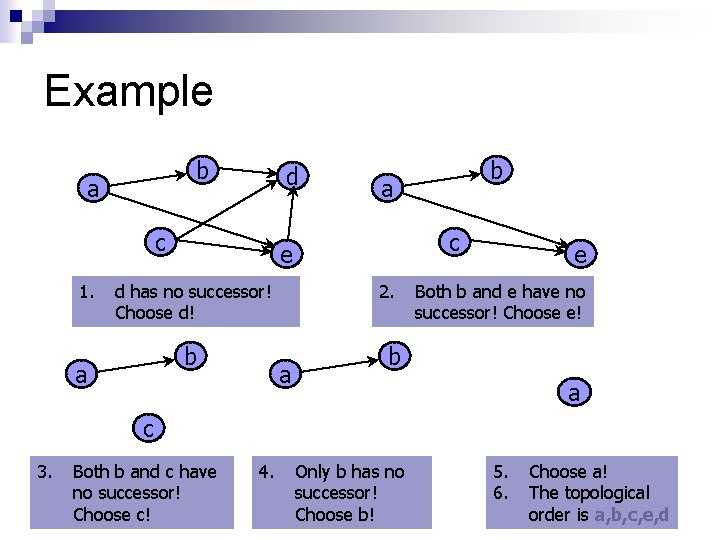
Example b a d c 1. b a a c e 2. d has no successor! Choose d! a b e Both b and e have no successor! Choose e! b a c 3. Both b and c have no successor! Choose c! 4. Only b has no successor! Choose b! 5. 6. Choose a! The topological order is a, b, c, e, d

Time analysis n n Finding a node with no successor takes O(|V|+|E|) time. We need to repeat this process |V| times. Total time = O(|V|2 + |V| |E|). We can implement the above process using DFS. The time can be improved to O(|V| + |E|).

Algorithm based on DFS Algorithm top. Sort 2 s. create. Stack(); for (all nodes v in the graph) { if (v has no predecessors) { s. push(v); mark v as visited; } } while (s is not empty) { let v be the node on the top of the stack s; if (no unvisited nodes are children to v) { // i. e. v has no unvisited successor a. List. add(1, v); s. pop(); // blacktrack } else { select an unvisited child u of v; s. push(u); mark u as visited; } } return a. List;

Bipartite Matching IOI/ACM ICPC Training June 2004

Unweighted Bipartite Matching

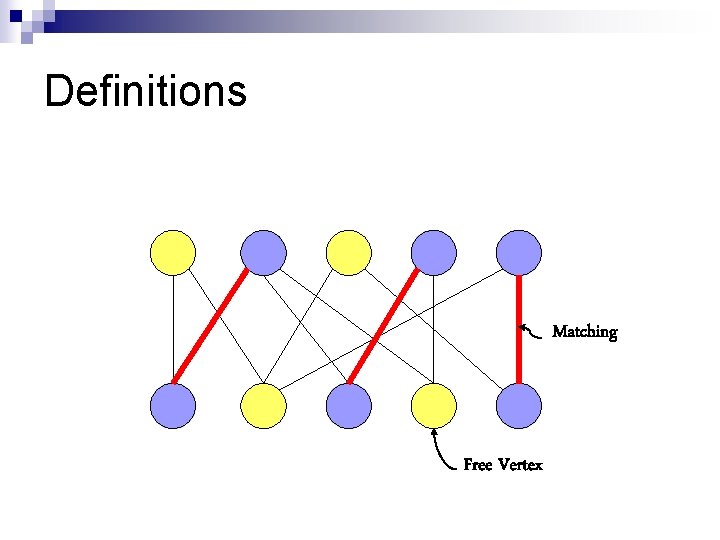
Definitions Matching Free Vertex

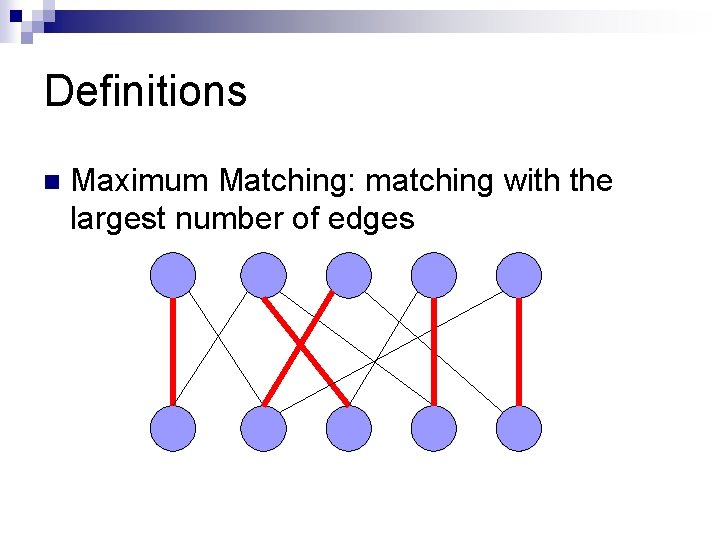
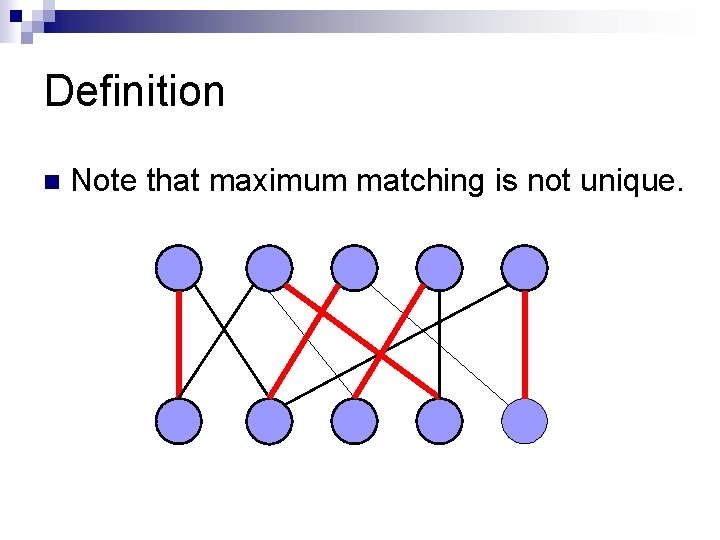
Definitions n Maximum Matching: matching with the largest number of edges

Definition n Note that maximum matching is not unique.

Intuition Let the top set of vertices be men n Let the bottom set of vertices be women n Suppose each edge represents a pair of man and woman who like each other n n Maximum matching tries to maximize the number of couples!

Applications n Matching has many applications. For examples, ¨ Comparing Evolutionary Trees ¨ Finding RNA structure ¨… n This lecture lets you know how to find maximum matching.

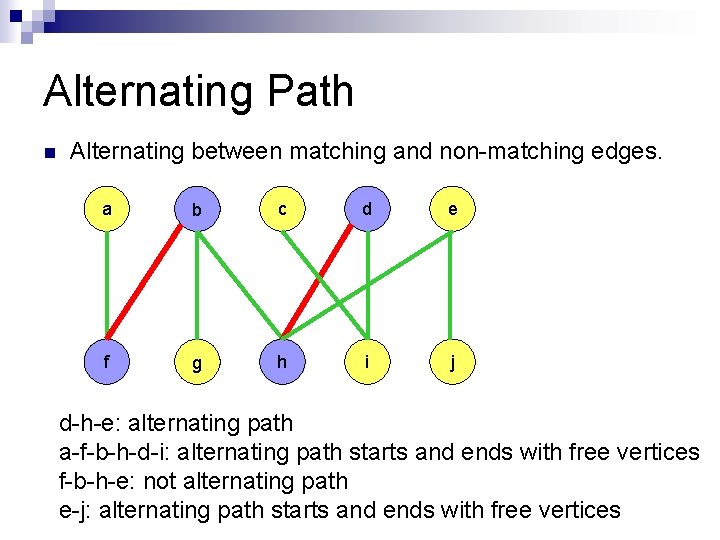
Alternating Path n Alternating between matching and non-matching edges. a b c d e f g h i j d-h-e: alternating path a-f-b-h-d-i: alternating path starts and ends with free vertices f-b-h-e: not alternating path e-j: alternating path starts and ends with free vertices

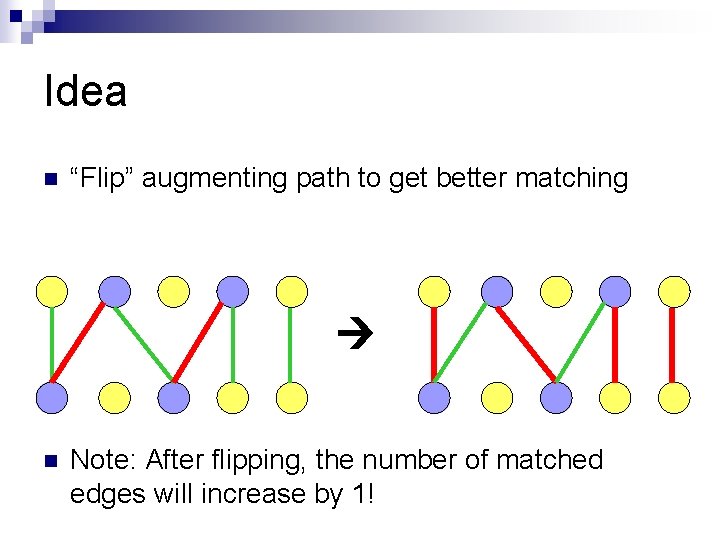
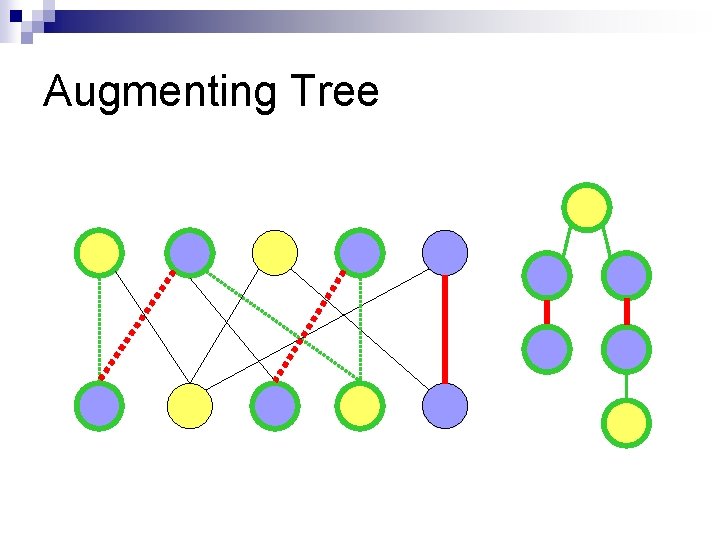
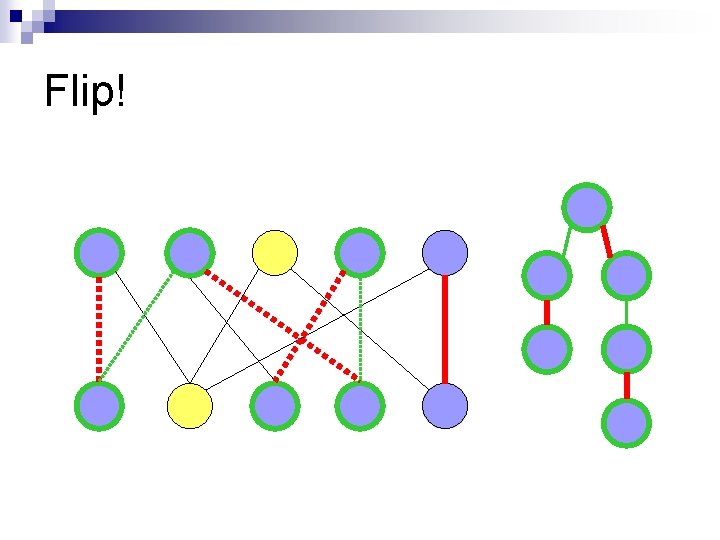
Idea n “Flip” augmenting path to get better matching n Note: After flipping, the number of matched edges will increase by 1!

Idea n Theorem (Berge 1975): A matching M in G is maximum iff There is no augmenting path Proof: n ( ) If there is an augmenting path, clearly not maximum. (Flip matching and non-matching edges in that path to get a “better” matching!)

Proof for the other direction n ( ) Suppose M is not maximum. Let M’ be a maximum matching such that |M’|>|M|. Consider H = M M’ = (M M’)-(M M’) i. e. a set of edges in M or M’ but not both H has two properties: ¨ Within H, number of edges belong to M’ > number of edges belong to M. ¨ H can be decomposed into a set of paths. All paths should be alternating between edges in M and M’. n There should exist a path with more edges from M’. Also, it is alternating.

Idea of Algorithm Start with an arbitrary matching n While we still can find an augmenting path n ¨ Find the augmenting path P ¨ Flip the edges in P

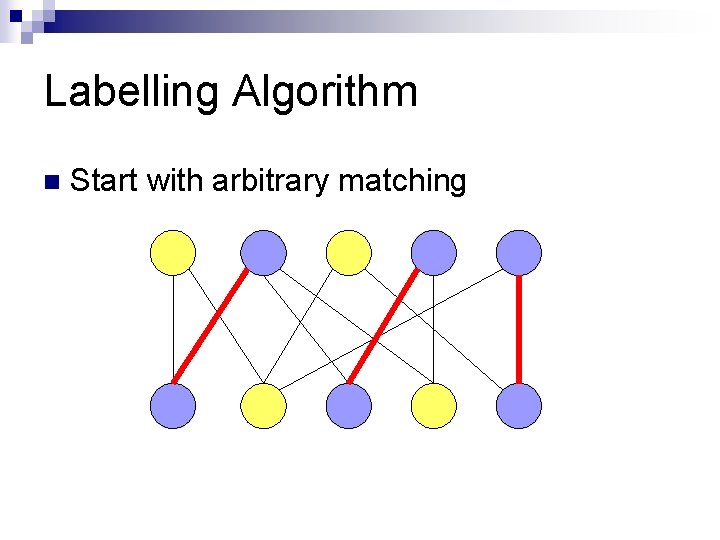
Labelling Algorithm n Start with arbitrary matching

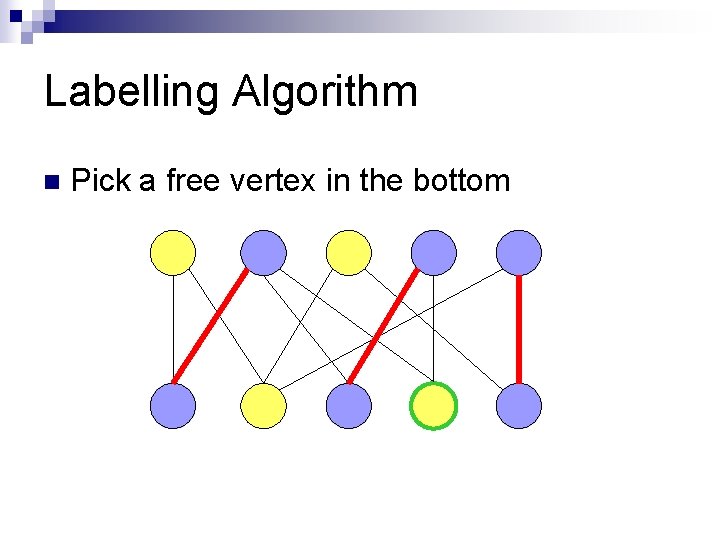
Labelling Algorithm n Pick a free vertex in the bottom

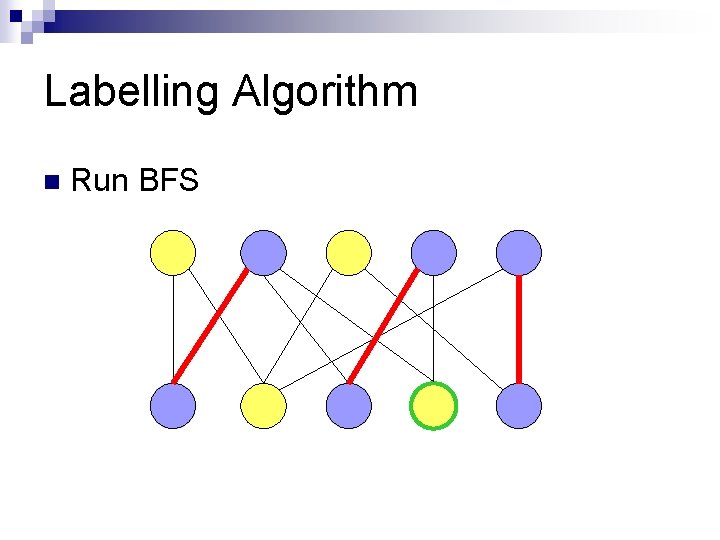
Labelling Algorithm n Run BFS

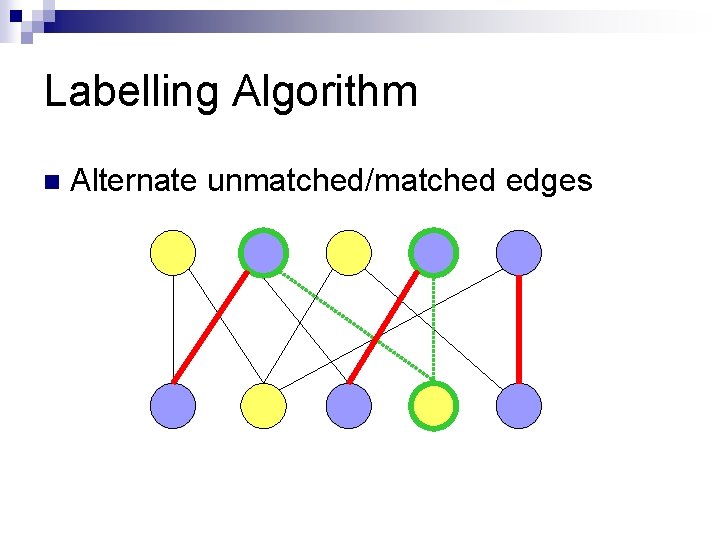
Labelling Algorithm n Alternate unmatched/matched edges

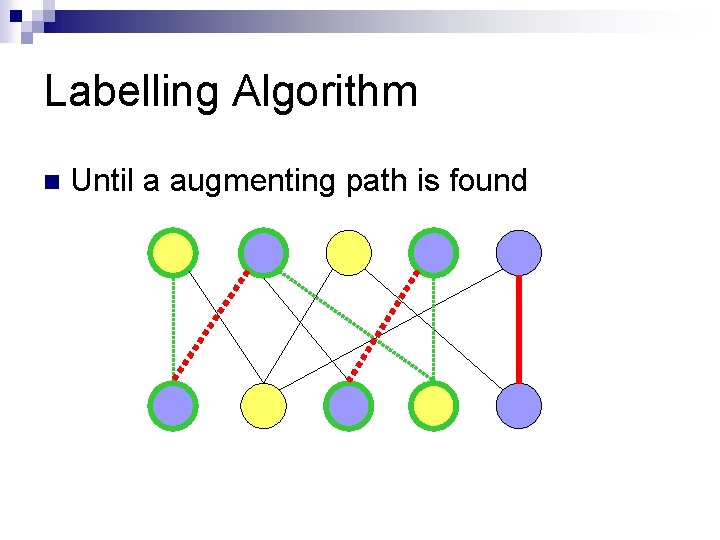
Labelling Algorithm n Until a augmenting path is found

Augmenting Tree

Flip!

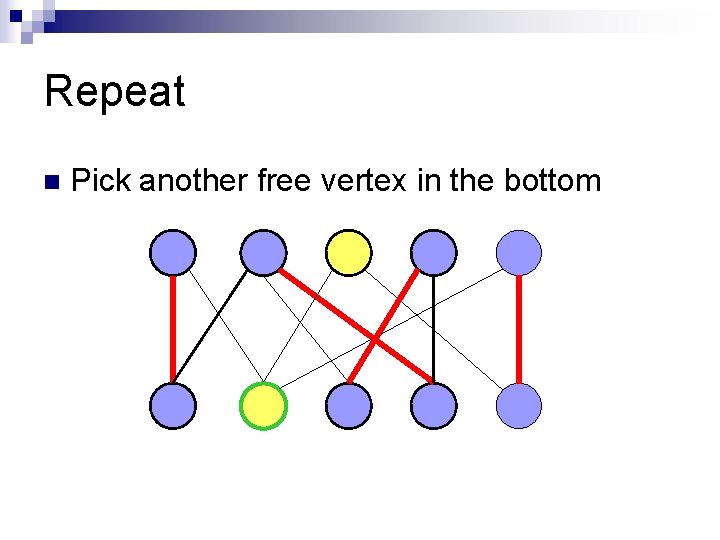
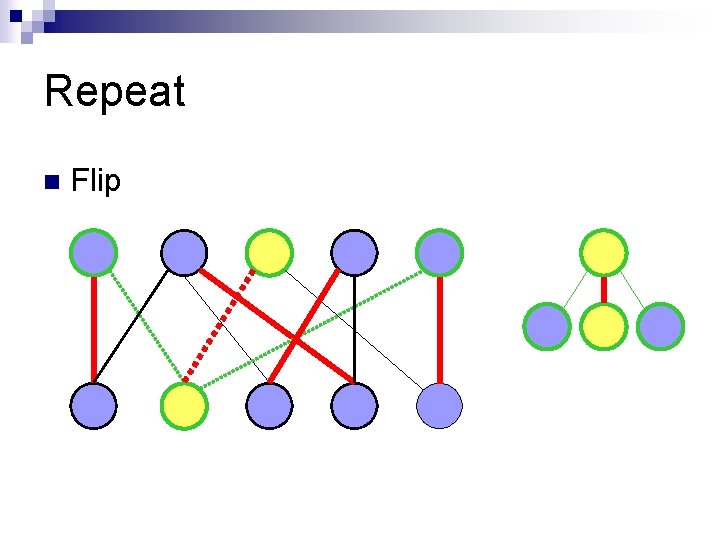
Repeat n Pick another free vertex in the bottom

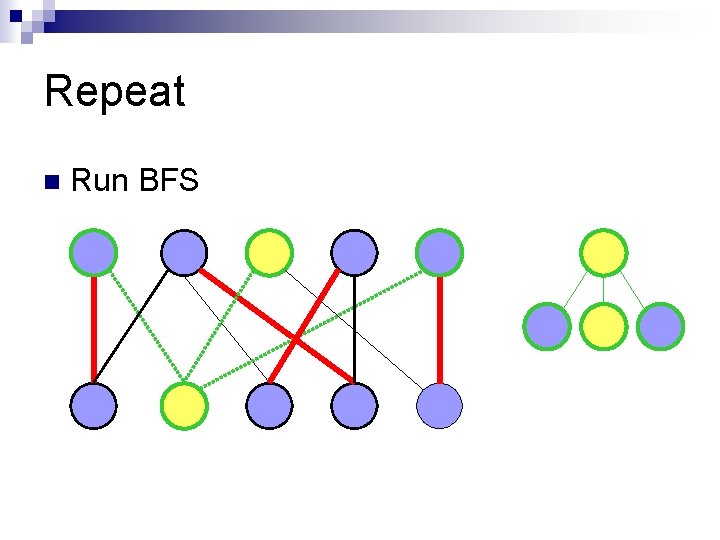
Repeat n Run BFS

Repeat n Flip

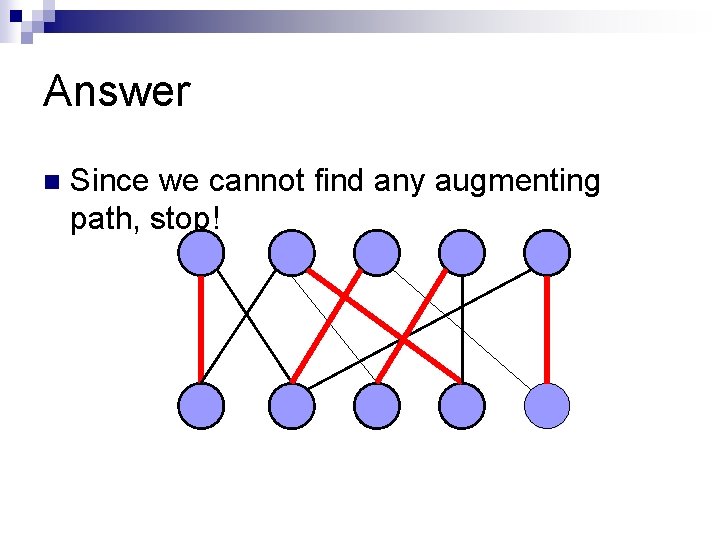
Answer n Since we cannot find any augmenting path, stop!

Overall algorithm n n Start with an arbitrary matching (e. g. , empty matching) Repeat forever ¨ For all free vertices in the bottom, n do bfs to find augmenting paths ¨ If found, then flip the edges ¨ If fail to find, stop and report the maximum matching.

Time analysis We can find at most |V| augmenting paths (why? ) n To find an augmenting path, we use bfs! Time required = O( |V| + |E| ) n Total time: O(|V|2 + |V| |E|) n

Improvement We can try to find augmenting paths in parallel for all free nodes in every iteration. n Using such approach, the time complexity is improved to O(|V|0. 5 |E|) n

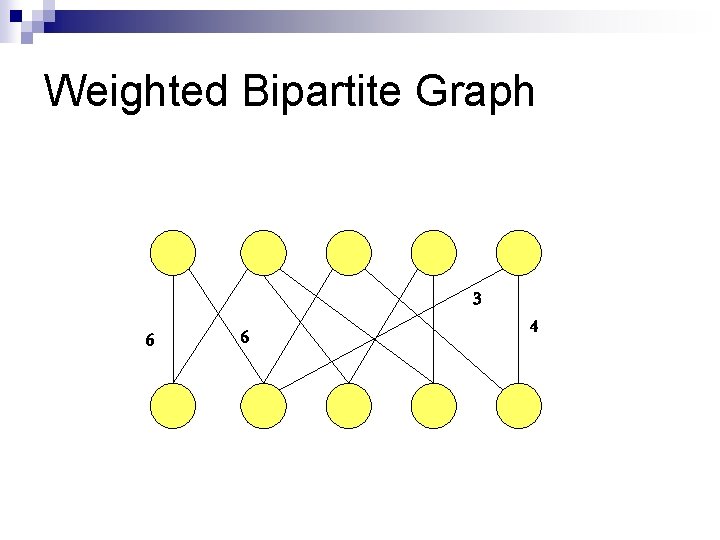
Weighted Bipartite Graph 3 6 6 4

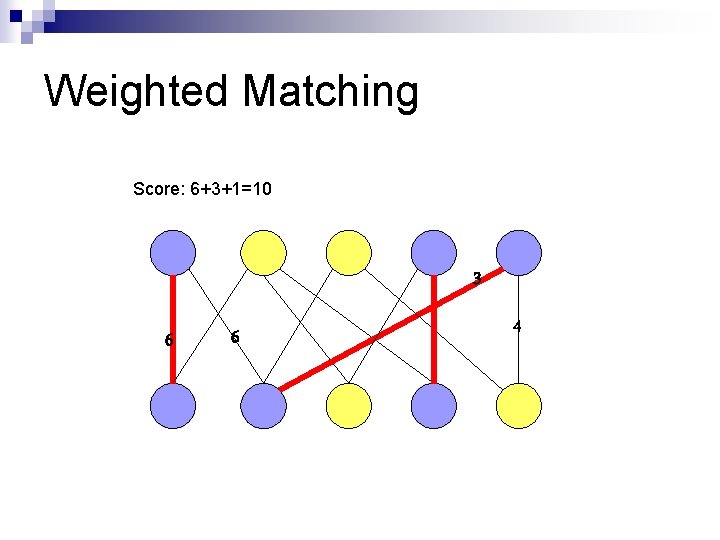
Weighted Matching Score: 6+3+1=10 3 6 6 4

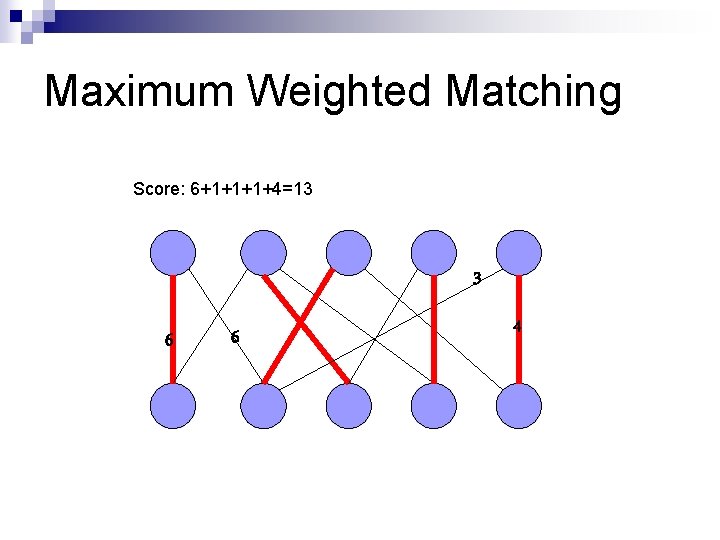
Maximum Weighted Matching Score: 6+1+1+1+4=13 3 6 6 4

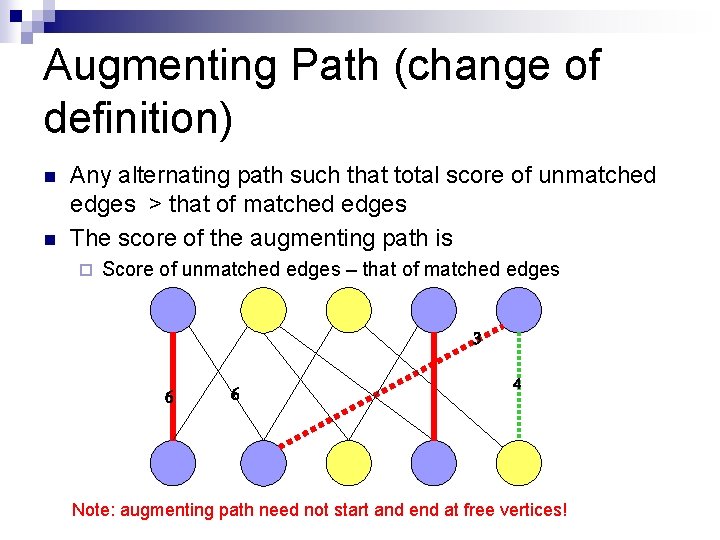
Augmenting Path (change of definition) n n Any alternating path such that total score of unmatched edges > that of matched edges The score of the augmenting path is ¨ Score of unmatched edges – that of matched edges 3 6 6 4 Note: augmenting path need not start and end at free vertices!

Idea for finding maximum weight matching n Theorem: Let M be a matching of maximum weight among matchings of size |M|. If P is an augmenting path for M of maximum weight, ¨ Then, the matching formed by augmenting M by P is a matching of maximum weight among matchings of size |M|+1. ¨

Overall Algorithm n n Start with an empty matching Repeat forever ¨ Find an augmenting path P with maximum score ¨ If the score > 0, then flip the edges ¨ Otherwise, stop and report the maximum weight matching.

Time analysis The same! n Time required = O(|V|2 + |V| |E|) n

Stable Marriage Problem IOI/ACM ICPC Training June 2004

Stable Marriage Problem Given N men and N women, each person list in order of preference all the people of the opposite sex who would like to marry. n Problem: n ¨ Engage all the women to all the men in such a way as to respect all their preferences as much as possible.

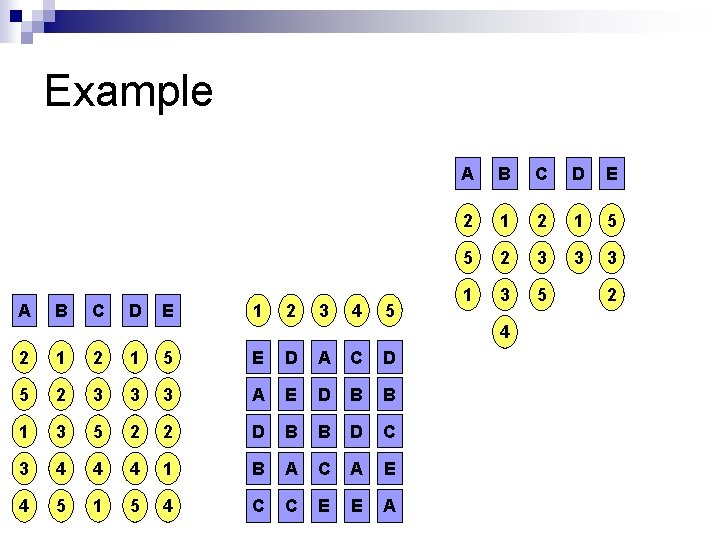
Stable? n A set of marriages is unstable if ¨ n two people who are not married both prefer each other than their spouses E. g. Suppose we have A 1 B 3 C 2 D 4 E 5. This is unstable since A prefer 2 more than 1 ¨ 2 prefer A more than C ¨ A B C D E 1 2 3 4 5 2 1 5 E D A C D 5 2 3 3 3 A E D B B 1 3 5 2 2 D B B D C 3 4 4 4 1 B A C A E 4 5 1 5 4 C C E E A

Naïve solution Starting from a feasible solution. n Check if it is stable. n ¨ If yes, done! ¨ If not, remove an unstable couple. n Is this work?

Naïve solution (2) n n Does not work! E. g. ¨ A 1 B 3 C 2 D 4 E 5 ¨ A 2 B 3 C 1 D 4 E 5 ¨ A 3 B 2 C 1 D 4 E 5 ¨ A 3 B 1 C 2 D 4 E 5 A B C D E 1 2 3 4 5 2 1 5 E D A C D 5 2 3 3 3 A E D B B 1 3 5 2 2 D B B D C 3 4 4 4 1 B A C A E 4 5 1 5 4 C C E E A

Solution 1. 2. 3. Let X be the first man. X proposes to the best woman in the remaining on his list. (Initially, the first woman on his list!) If α is not engaged ¨ 4. If α prefers X more than her fiancee Y, ¨ 5. Pair up (X, α). Then, set X=next man and goto 1. Pair up (X, α). Then, set X=Y and goto 1. Goto 1

Example A B C D E 1 2 3 4 5 A B C D E 2 1 5 5 2 3 3 3 1 3 5 4 2 1 5 E D A C D 5 2 3 3 3 A E D B B 1 3 5 2 2 D B B D C 3 4 4 4 1 B A C A E 4 5 1 5 4 C C E E A 2

Time analysis n If there are N men and N women, ¨ O(N 2) time

Algorithm n n n prefer[m][s]=w means the woman w is on the sth position in the preference list of the man m Let next[m] be the current best woman in his remaining list. (Initially, next[m]=0) fiancee[w]=m means the man m engaged to woman w. (Initially, fiancee[w]=0) Let rank[w][m] is the ranking of the man m in the preference list of the woman w. For(m=1; m<=N; m++) { For(s=m; s!=0; }