ALJABAR LINIER MATRIKS PENGERTIAN MATRIKS Matriks adalah himpunan

ALJABAR LINIER & MATRIKS

PENGERTIAN MATRIKS • Matriks adalah himpunan skalar (bilangan riil atau kompleks) yang disusun atau dijajarkan secara empat persegi panjang menurut baris-baris dan kolom-kolom • Matriks adalah jajaran elemen (berupa bilangan) berbentuk empat persegi panjang • Matriks adalah himpumam suatu bilangan yang disusun dalam bentuk persegi panjang yang memuat baris-baris dan kolom-kolom • Bilangan tersebut disebut entri / elemen

NOTASI MATRIKS • Lambang matrik huruf besar • Lambang elemen huruf kecil • Notasi yang dipakai: atau

NOTASI MATRIK Baris ke -1 • A = Unsur / entri /elemen kemn (baris m kolom n) Kolom ke -2 Matrik A berukuran (ordo) m x n Misalkan A dan B adalah matriks berukuran sama, A dan B dikatakan sama (notasi A = B) Jika untuk setiap i dan j

JENIS MATRIKS • MATRIKS NOL, adalah matriks yang semua elemennya nol § Sifat-sifat : ü A+0=A, jika ukuran matriks A = ukuran matriks 0 ü A*0=0, begitu juga 0*A=0. • MATRIKS BUJURSANGKAR, adalah matriks yang jumlah baris dan jumlah kolomnya sama. Barisan elemen a 11, a 22, a 33, …. ann disebut diagonal utama dari matriks bujursangkar A tersebut. Contoh : Matriks berukuran 2 x 2 A=

• MATRIKS DIAGONAL, adalah matriks bujursangkar yang semua elemen diluar diagonal utamanya nol. Contoh : • MATRIKS SATUAN/IDENTITY, adalah matriks diagonal yang semua elemen diagonalnya adalah 1. Contoh : • Sifat-sifat matriks identitas : A*I=A , I*A=A

• MATRIKS SKALAR, adalah matriks diagonal yang semua elemennya sama tetapi bukan nol atau satu. Contoh : A= • MATRIKS SEGITIGA ATAS (UPPER TRIANGULAR), adalah matriks bujursangkar yang semua elemen dibawah diagonal elemennya = 0. A=

• MATRIKS SEGITIGA BAWAH (LOWER TRIANGULAR), adalah matriks bujursangkar yang semua elemen diatas diagonal elemennya = 0. A=

• MATRIKS SIMETRIS, adalah matriks bujursangkar yang elemennya simetris secara diagonal. Dapat juga dikatakan bahwa matriks simetris adalah matriks yang transposenya sama dengan dirinya sendiri. Contoh : A= =

• MATRIKS ANTISIMETRIS, adalah matriks yang transposenya adalah negatif dari matriks tersebut. Maka AT=-A dan aij=-aij, elemen diagonal utamanya = 0 Contoh :
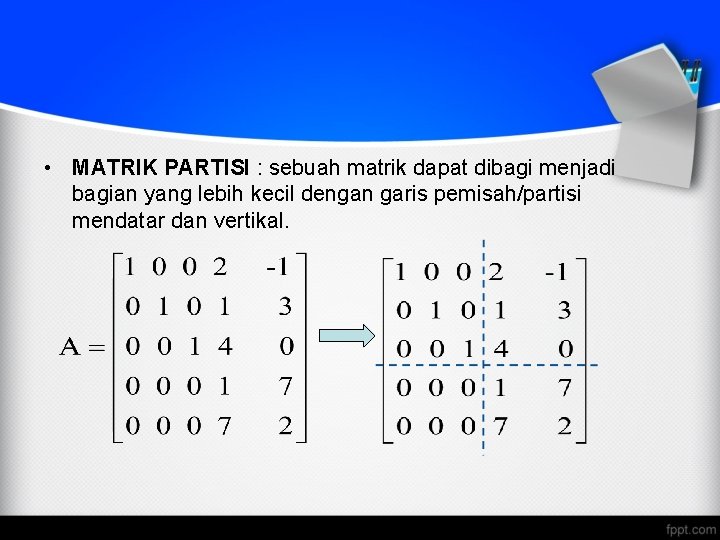
• MATRIK PARTISI : sebuah matrik dapat dibagi menjadi bagian yang lebih kecil dengan garis pemisah/partisi mendatar dan vertikal.

MATRIK PARTISI dimana: • I adalah matrik identitas 3 x 3, • B adalah matrik 3 x 2 • O adalah matrik nol 2 x 3 • C adalah matrik 2 x 2 Dengan cara partisi tersebut, kita dapat lihat bahwa matrik A adalah sebagai matrik 2 x 2

OPERASI MATRIKS • Penjumlahan Matriks Syarat : Dua matriks berordo sama dapat dijumlahkan Contoh = a. b.
![• Sifat-sifat penjumlahan Matriks • [ A ] + [ B ] = • Sifat-sifat penjumlahan Matriks • [ A ] + [ B ] =](http://slidetodoc.com/presentation_image_h2/5f9c66cacd604b537f4e43fdbf71817c/image-14.jpg)
• Sifat-sifat penjumlahan Matriks • [ A ] + [ B ] = [ B ] + [ A ] Komutatif • [ A ] + [ B ] + [ C ] = ([ A ] + [ B ]) + [ C ] Assosiatif

• Pengurangan Matriks Syarat : Dua matriks berordo sama dapat dkurangkan Contoh = a. b.

• Perkalian Matriks ü Perkalian Skalar dengan Matriks Contoh : ü Perkalian Matriks dengan Matriks Misalkan A berordo pxq dan B berordo mxn Syarat : A X B haruslah q = m , hasil perkalian AB , berordo pxn
![• Sifat-sifat perkalian skalar matrik: k ( [A] + [B] ) = k • Sifat-sifat perkalian skalar matrik: k ( [A] + [B] ) = k](http://slidetodoc.com/presentation_image_h2/5f9c66cacd604b537f4e43fdbf71817c/image-17.jpg)
• Sifat-sifat perkalian skalar matrik: k ( [A] + [B] ) = k [A] + k [B] k ( [A] + [B] ) = ( [A] + [B] ) k
![• Sifat-sifat perkalian matrik: • [A] ( [B] + [C] ) = [A] • Sifat-sifat perkalian matrik: • [A] ( [B] + [C] ) = [A]](http://slidetodoc.com/presentation_image_h2/5f9c66cacd604b537f4e43fdbf71817c/image-18.jpg)
• Sifat-sifat perkalian matrik: • [A] ( [B] + [C] ) = [A] [B] + [A] [C] sifat distributif • ( [A] + [B] ) + [C] = [A] [B] + [A] [C] sifat distributif • [A] ( [B] [C] ) = ( [A] [B] ) [C] sifat assosiatif • [A] [B] ≠ [B] [A]

Latihan

TUGAS 1 1. Diberikan matriks – matriks sebagai berikut: Jika mungkin, maka hitunglah a. AB d. CB + D b. BA e. AB + DF c. A(C + E) f. (D + F)A g. BA + FD h. A(BD)

TUGAS 2
- Slides: 21