Alignment of beamlines using xray beam K Klementiev

Alignment of beamlines using x-ray beam K. Klementiev, ALBA/CELLS • is complement to mechanical alignment • uses the optics components themselves + beam diagnostics • is periodically done on every beamline Outline: • Introduction • Available tools for beamline alignment • Ray tracing of misaligned beamline (XAS) • Entangled misalignments • Alignment strategy 21. 10. 2008 1

Introduction What others have done? • There a very few papers and web-pages on the topic “Alignment of synchrotron beamlines”. Most of them are aimed at automatic alignment. • There is The Automatic Beamline Alignment Project in ESRF (Olof Svensson et al). It is aimed at algorithms and software. What I intend to present? • not an automatic procedure, but rather basic understanding of misaligned optics; • to stress the importance of ray tracing for studying misalignments of various kind; • to notice the usefulness of the monochromator as a kind of diagnostics device (never mentioned in literature, although some people use this); • a (general) strategy for initial beamline alignment. 21. 10. 2008 2

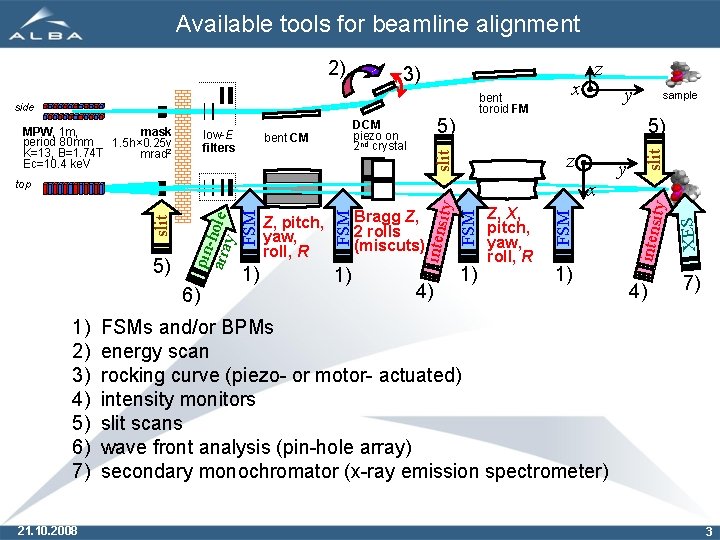
Available tools for beamline alignment low-E filters 5) DCM piezo on 2 nd crystal bent CM x 6) 1) 2) 3) 4) 5) 6) 7) 21. 10. 2008 1) 4) 1) Z, X, pitch, yaw, roll, R FSM ity FSM FSM 1) Bragg Z, 2 rolls (miscuts) intens 5) pinarra hole y slit top Z, pitch, yaw, roll, R sample 5) z slit MPW, 1 m, mask period 80 mm 1. 5 h× 0. 25 v K=13, B=1. 74 T mrad 2 Ec=10. 4 ke. V y 1) y 4) XES side x slit bent toroid FM z ity 3) intens 2) 7) FSMs and/or BPMs energy scan rocking curve (piezo- or motor- actuated) intensity monitors slit scans wave front analysis (pin-hole array) secondary monochromator (x-ray emission spectrometer) 3

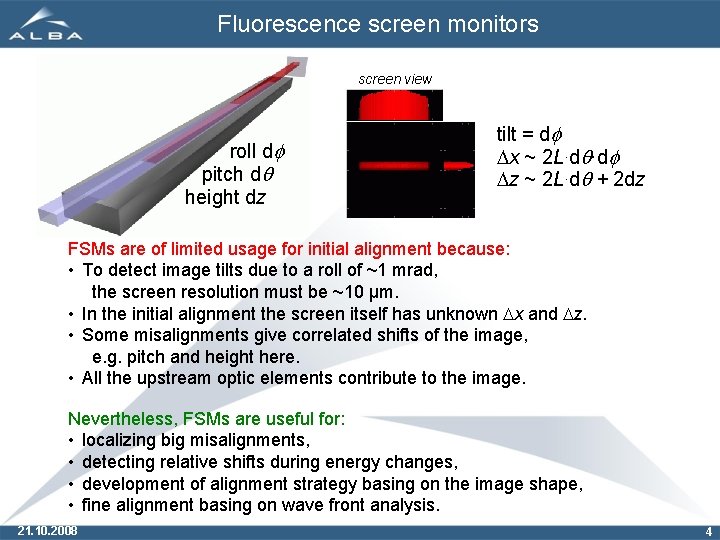
Fluorescence screen monitors screen view roll df pitch dq height dz tilt = df Dx ~ 2 L·dq·df Dz ~ 2 L·dq + 2 dz FSMs are of limited usage for initial alignment because: • To detect image tilts due to a roll of ~1 mrad, the screen resolution must be ~10 µm. • In the initial alignment the screen itself has unknown Dx and Dz. • Some misalignments give correlated shifts of the image, e. g. pitch and height here. • All the upstream optic elements contribute to the image. Nevertheless, FSMs are useful for: • localizing big misalignments, • detecting relative shifts during energy changes, • development of alignment strategy basing on the image shape, • fine alignment basing on wave front analysis. 21. 10. 2008 4

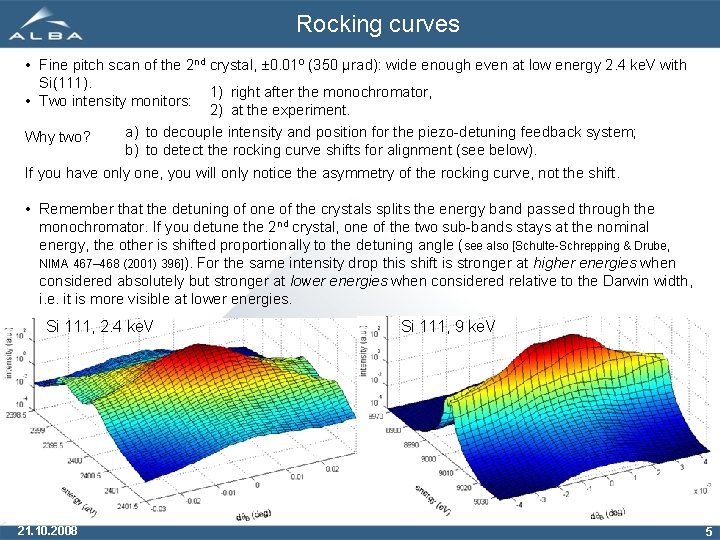
Rocking curves • Fine pitch scan of the 2 nd crystal, ± 0. 01º (350 µrad): wide enough even at low energy 2. 4 ke. V with Si(111). 1) right after the monochromator, • Two intensity monitors: 2) at the experiment. a) to decouple intensity and position for the piezo-detuning feedback system; Why two? b) to detect the rocking curve shifts for alignment (see below). If you have only one, you will only notice the asymmetry of the rocking curve, not the shift. • Remember that the detuning of one of the crystals splits the energy band passed through the monochromator. If you detune the 2 nd crystal, one of the two sub-bands stays at the nominal energy, the other is shifted proportionally to the detuning angle (see also [Schulte-Schrepping & Drube, NIMA 467– 468 (2001) 396]). For the same intensity drop this shift is stronger at higher energies when considered absolutely but stronger at lower energies when considered relative to the Darwin width, i. e. it is more visible at lower energies. Si 111, 2. 4 ke. V 21. 10. 2008 Si 111, 9 ke. V 5

Ray tracing of misaligned beamline (XAS) • Click the buttons below to invoke the corresponding presentations. • Ray tracing was done at 4 different energies (see the 4 columns) • For each energy (column) there are two animated beam images: 1) behind the detuned optical element; 2) at the sample position. All animations are synchronized, i. e. for the same detuning at a time. • The rocking curves are recorded at the two positions: a) after the DCM, b) at the sample. • The rocking curves are shown as i. two 3 D surfaces (for “a” and “b” rocking curves) in order to see if there is a maximum over the detuning coordinate, ii. as usual 2 D plots (in the lowest row) to mimic the real measurements of rocking curves; the “a” rocking curves are normalized to 1 and the “b” rocking curves are normalized to ½. Collimating Mirror (Optical. Alignment-1 -CM. ppt) 21. 10. 2008 DCM (Optical. Alignment-2 -DCM. ppt) Focusing Mirror (Optical. Alignment-3 -FM. ppt) 6

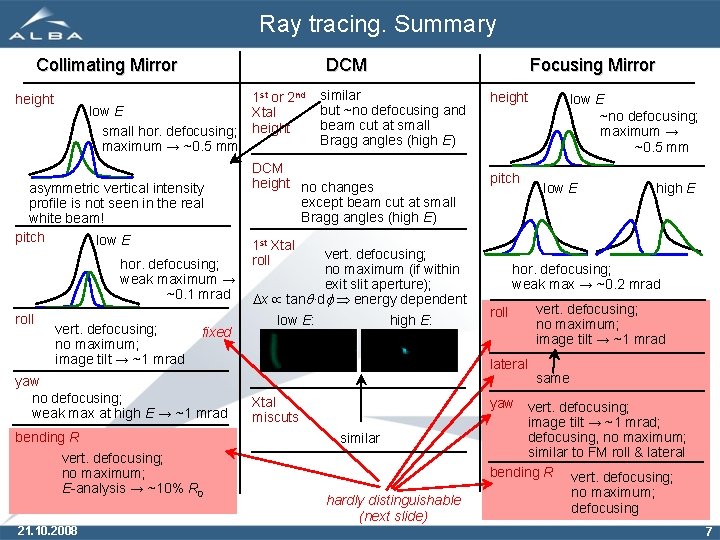
Ray tracing. Summary Collimating Mirror height DCM low E small hor. defocusing; maximum → ~0. 5 mm asymmetric vertical intensity profile is not seen in the real white beam! pitch low E hor. defocusing; weak maximum → ~0. 1 mrad roll vert. defocusing; no maximum; image tilt → ~1 mrad fixed yaw no defocusing; weak max at high E → ~1 mrad bending R vert. defocusing; no maximum; E-analysis → ~10% R 0 21. 10. 2008 1 st or 2 nd Xtal height similar but ~no defocusing and beam cut at small Bragg angles (high E) DCM height no changes except beam cut at small Bragg angles (high E) Focusing Mirror height pitch 1 st Xtal roll vert. defocusing; no maximum (if within exit slit aperture); Dx tanq·df energy dependent low E: high E: similar hardly distinguishable (next slide) low E high E hor. defocusing; weak max → ~0. 2 mrad roll lateral Xtal miscuts low E ~no defocusing; maximum → ~0. 5 mm vert. defocusing; no maximum; image tilt → ~1 mrad same yaw vert. defocusing; image tilt → ~1 mrad; defocusing, no maximum; similar to FM roll & lateral bending R vert. defocusing; no maximum; defocusing 7

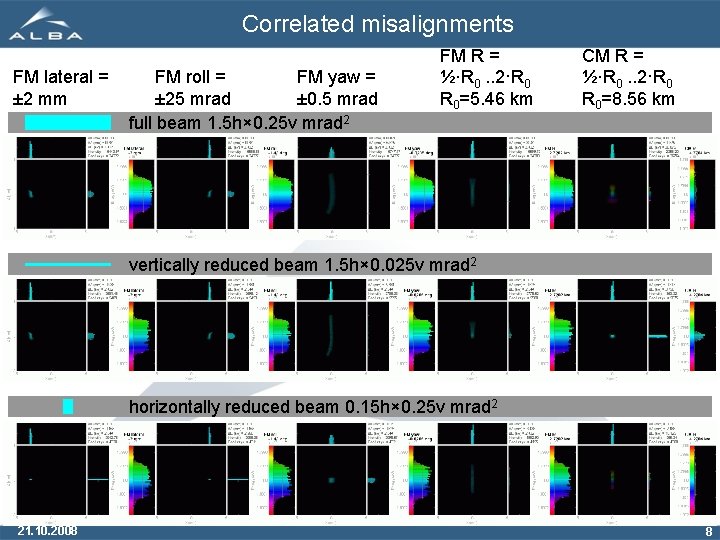
Correlated misalignments FM lateral = ± 2 mm FM roll = FM yaw = ± 25 mrad ± 0. 5 mrad full beam 1. 5 h× 0. 25 v mrad 2 FM R = ½·R 0. . 2·R 0 R 0=5. 46 km CM R = ½·R 0. . 2·R 0 R 0=8. 56 km vertically reduced beam 1. 5 h× 0. 025 v mrad 2 horizontally reduced beam 0. 15 h× 0. 25 v mrad 2 21. 10. 2008 8

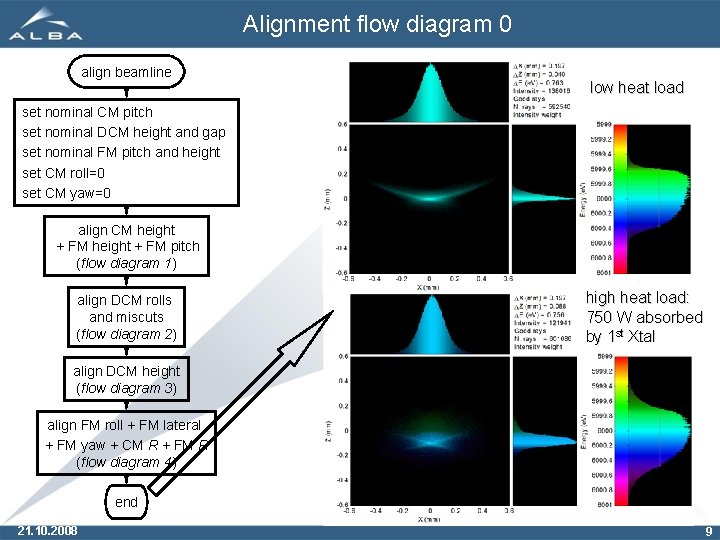
Alignment flow diagram 0 align beamline low heat load set nominal CM pitch set nominal DCM height and gap set nominal FM pitch and height set CM roll=0 set CM yaw=0 align CM height + FM pitch (flow diagram 1) align DCM rolls and miscuts (flow diagram 2) high heat load: 750 W absorbed by 1 st Xtal align DCM height (flow diagram 3) align FM roll + FM lateral + FM yaw + CM R + FM R (flow diagram 4) end 21. 10. 2008 9

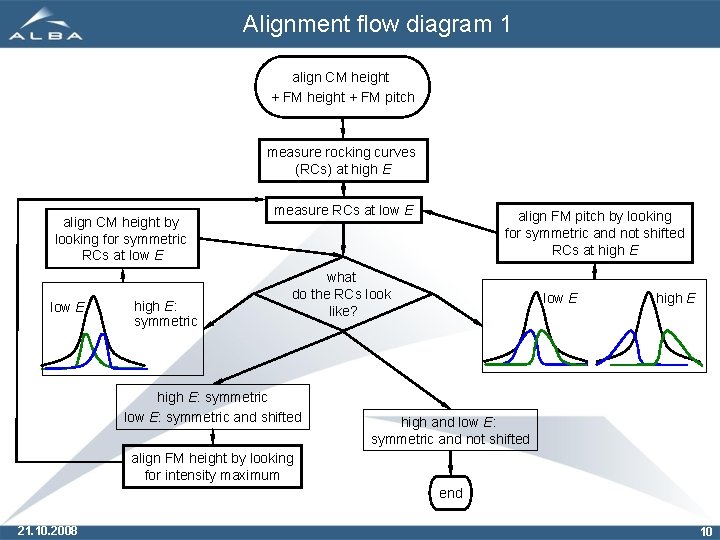
Alignment flow diagram 1 align CM height + FM pitch measure rocking curves (RCs) at high E align CM height by looking for symmetric RCs at low E high E: symmetric measure RCs at low E align FM pitch by looking for symmetric and not shifted RCs at high E what do the RCs look like? high E: symmetric low E: symmetric and shifted low E high and low E: symmetric and not shifted align FM height by looking for intensity maximum end 21. 10. 2008 10

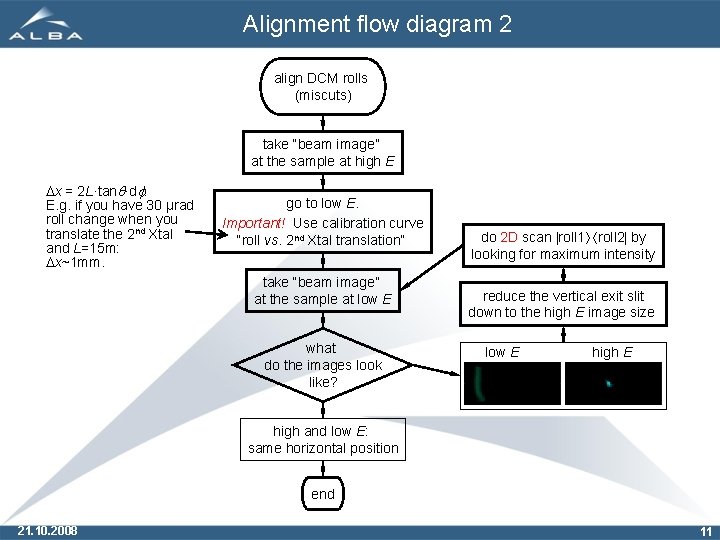
Alignment flow diagram 2 align DCM rolls (miscuts) take “beam image” at the sample at high E Dx = 2 L·tanq·df. E. g. if you have 30 µrad roll change when you translate the 2 nd Xtal and L=15 m: Dx~1 mm. go to low E. Important! Use calibration curve “roll vs. 2 nd Xtal translation” take “beam image” at the sample at low E what do the images look like? do 2 D scan roll 1 roll 2 by looking for maximum intensity reduce the vertical exit slit down to the high E image size low E high and low E: same horizontal position end 21. 10. 2008 11

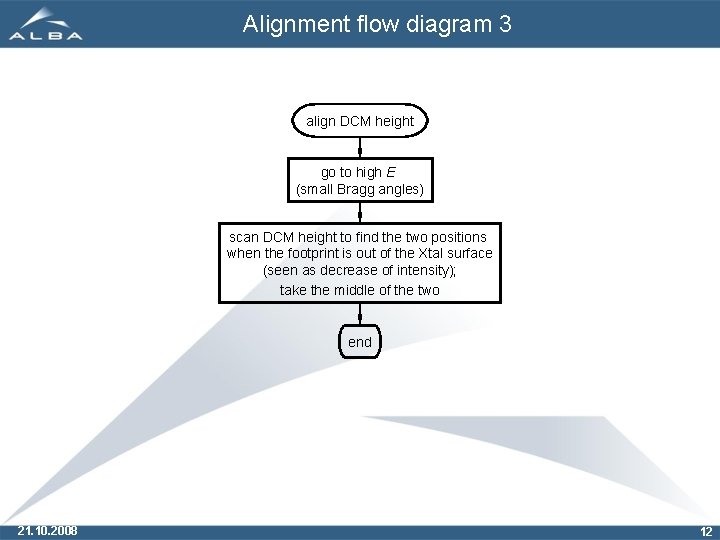
Alignment flow diagram 3 align DCM height go to high E (small Bragg angles) scan DCM height to find the two positions when the footprint is out of the Xtal surface (seen as decrease of intensity); take the middle of the two end 21. 10. 2008 12

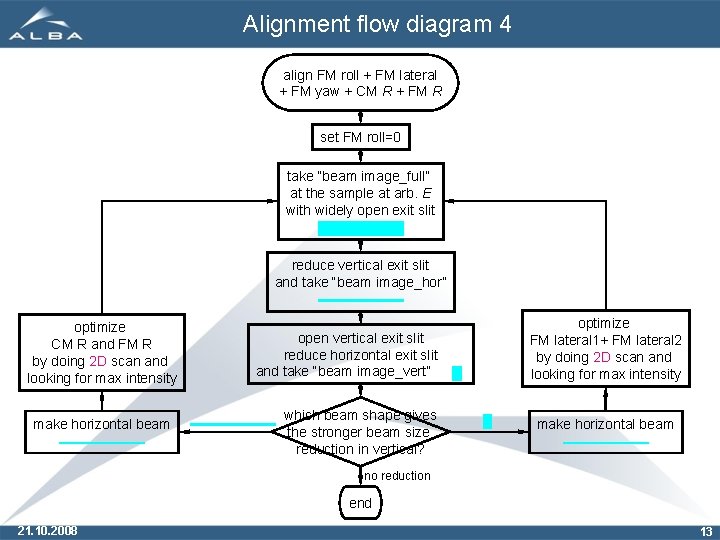
Alignment flow diagram 4 align FM roll + FM lateral + FM yaw + CM R + FM R set FM roll=0 take “beam image_full” at the sample at arb. E with widely open exit slit reduce vertical exit slit and take “beam image_hor” optimize CM R and FM R by doing 2 D scan and looking for max intensity make horizontal beam open vertical exit slit reduce horizontal exit slit and take “beam image_vert” which beam shape gives the stronger beam size reduction in vertical? optimize FM lateral 1+ FM lateral 2 by doing 2 D scan and looking for max intensity make horizontal beam no reduction end 21. 10. 2008 13

Q&A What are the generalities for all beamlines ? • Rocking curves are asymmetric under motion of mirrors and crystal into/out of the beam. E. g. if you have an intensity monitor upstream your KB system, you can easily decouple at least 2 of the N (=7? 8? ) degrees of freedom. • Miscut and roll misalignment in crystals lead to energy-dependent horizontal shifts. This presentation is about a hard x-ray beamline. What would differ for a soft one? • Don’t know. How to repeat the ray tracing for another beamline? • The Matlab scripts are freely available. Prepare Shadow projects for different energies in the way that the OE positions are fixed and coincide with the physical ones. Ask me for further help. Outlook • Ray tracing with the pinhole array at defocusing/de-collimating conditions and thermal bumps. • Programs for pinhole image analysis + inverse problem. May I have a student for this? • Eventually, automatic beamline alignment based on the pinhole images. Thanks • to J. Nicolás for introduction into the analysis of the imaging properties by means of the path function. Using his approach (ask him for the article) and the tools like Mathematica one can analyze the images without ray tracing. I don’t know what is easier though. 19. 09. 2008 21. 10. 2008 14