Alignment Introduction Notes courtesy of Funk et al

Alignment Introduction Notes courtesy of Funk et al. , SIGGRAPH 2004

Outline: • Challenge • General Approaches • Specific Examples

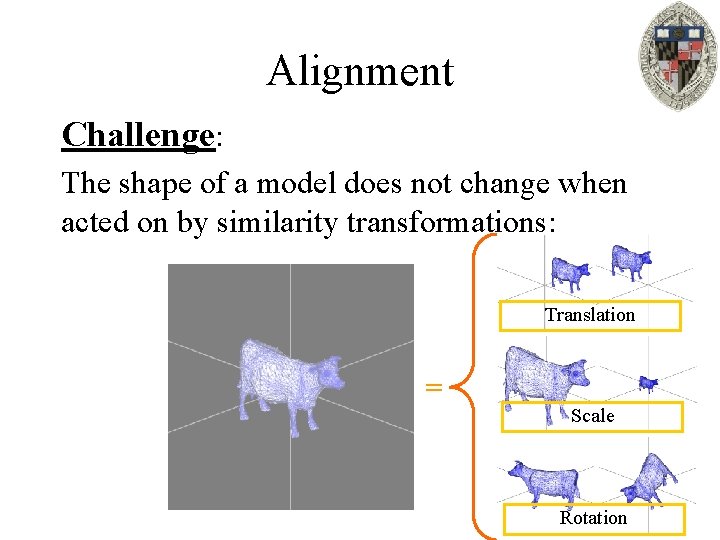
Alignment Challenge: The shape of a model does not change when acted on by similarity transformations: Translation = Scale Rotation

Alignment Challenge: However, the shape descriptors can change if a the model is: – Translated – Scaled – Rotated How do we match shape descriptors across transformations that do not change the shape of a model?

Outline: • Challenge • General Approaches • Specific Examples

Alignment Approaches: Given the shape descriptors of two models, find the transformation(s) -- translation, scale, and rotation -that minimize the distance between the two models: – Exhaustive search – Closed form solution – Minimization – Normalization – Invariance

Alignment Aside: Because translations and rotations preserve distances, applying such a transformation to one model is equivalent to applying the inverse transformation to the other one: =

Alignment Aside: For translations and rotations we can simplify the alignment equation:

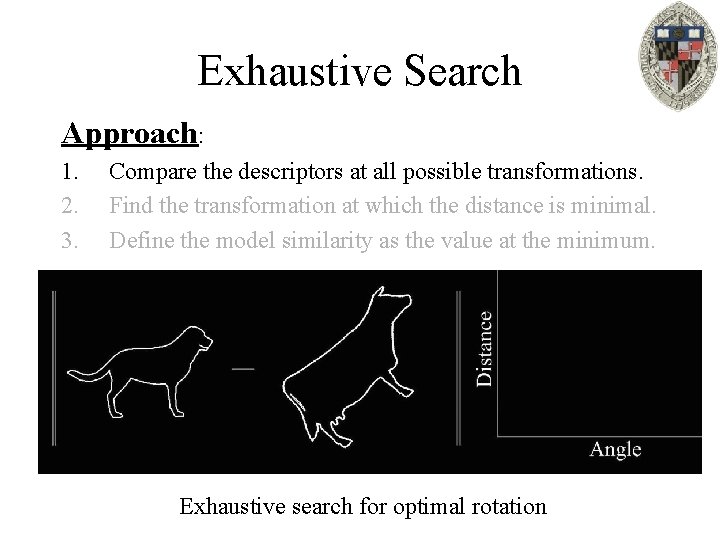
Exhaustive Search Approach: 1. 2. 3. Compare the descriptors at all possible transformations. Find the transformation at which the distance is minimal. Define the model similarity as the value at the minimum.

Exhaustive Search Approach: 1. 2. 3. Compare the descriptors at all possible transformations. Find the transformation at which the distance is minimal. Define the model similarity as the value at the minimum. Exhaustive search for optimal rotation

Exhaustive Search Approach: 1. 2. 3. Compare the descriptors at all possible transformations. Find the transformation at which the distance is minimal. Define the model similarity as the value at the minimum.

Exhaustive Search Properties: C Always gives the correct answer D Needs to be performed at run-time and can be very slow to compute: Computes the measure of similarity for every transform. We only need the value at the best one.

Closed Form Solution Approach: Explicitly find the transformation(s) that solves the equation: Properties: C C D D Always gives the correct answer Only compute the measure of similarity for the best transformation. A closed form solution does not always exist. Often needs to be computed at run-time.

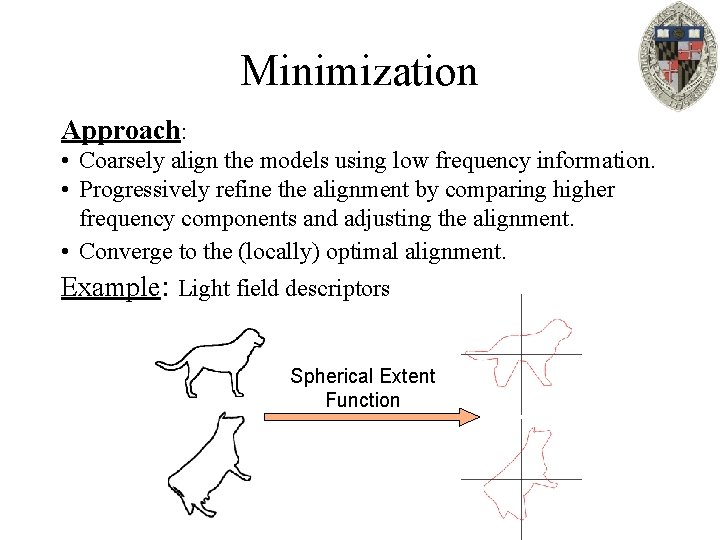
Minimization Approach: • Coarsely align the models using low frequency information. • Progressively refine the alignment by comparing higher frequency components and adjusting the alignment. • Converge to the (locally) optimal alignment. Example: Light field descriptors Spherical Extent Function

Minimization Approach: • Coarsely align the models using low frequency information. • Progressively refine the alignment by comparing higher frequency components and adjusting the alignment. • Converge to the (locally) optimal alignment. Initial Models Low Frequency Aligned Models

Minimization Approach: • Coarsely align the models using low frequency information. • Progressively refine the alignment by comparing higher frequency components and adjusting the alignment. • Converge to the (locally) optimal alignment. Initial Models = + Low Frequency High Frequency Aligned Models

Minimization Properties: C D D Can be applied to any type of transformation Needs to be computed at run-time. Difficult to do robustly: Given the low frequency alignment and the computed highfrequency alignment, how do you combine the two? Considerations can include: • • • Relative size of high and low frequency info Distribution of info across the low frequencies Speed of oscillation

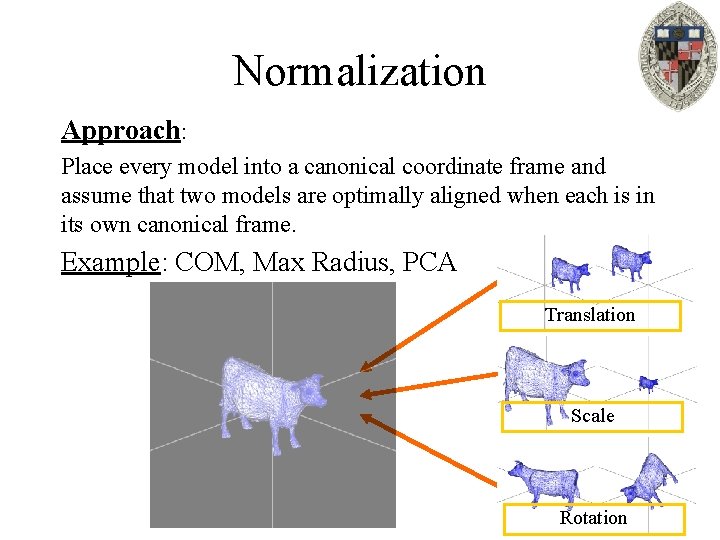
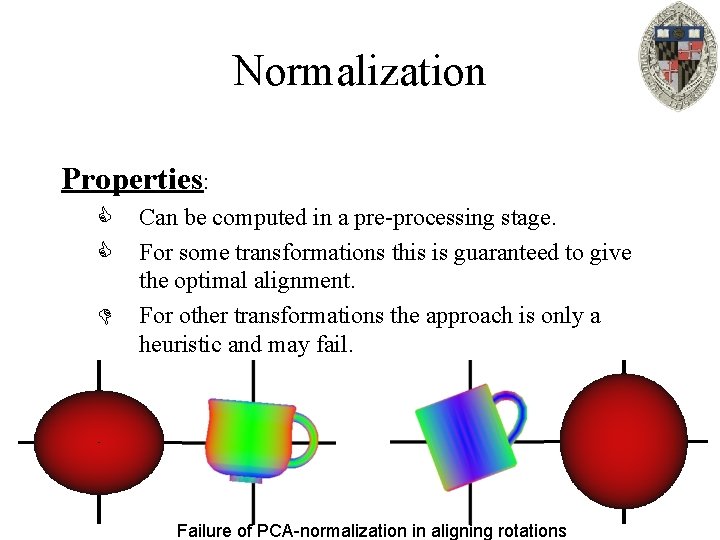
Normalization Approach: Place every model into a canonical coordinate frame and assume that two models are optimally aligned when each is in its own canonical frame. Example: COM, Max Radius, PCA Translation Scale Rotation

Normalization Properties: C C D Can be computed in a pre-processing stage. For some transformations this is guaranteed to give the optimal alignment. For other transformations the approach is only a heuristic and may fail. Failure of PCA-normalization in aligning rotations

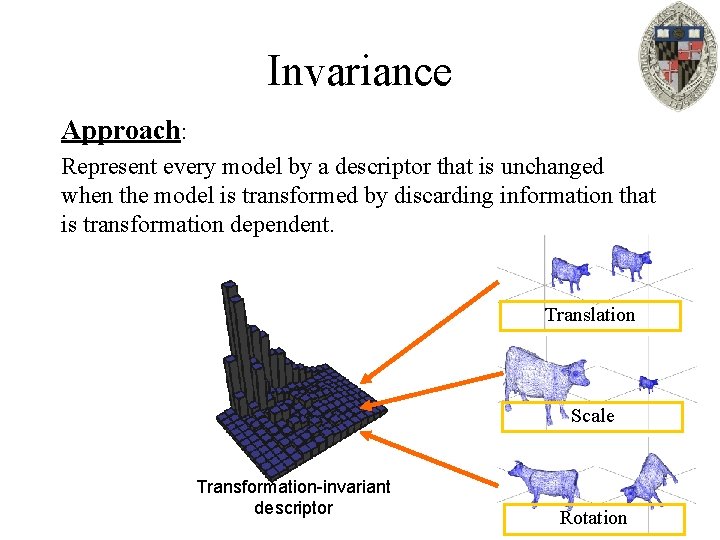
Invariance Approach: Represent every model by a descriptor that is unchanged when the model is transformed by discarding information that is transformation dependent. Translation Scale Transformation-invariant descriptor Rotation

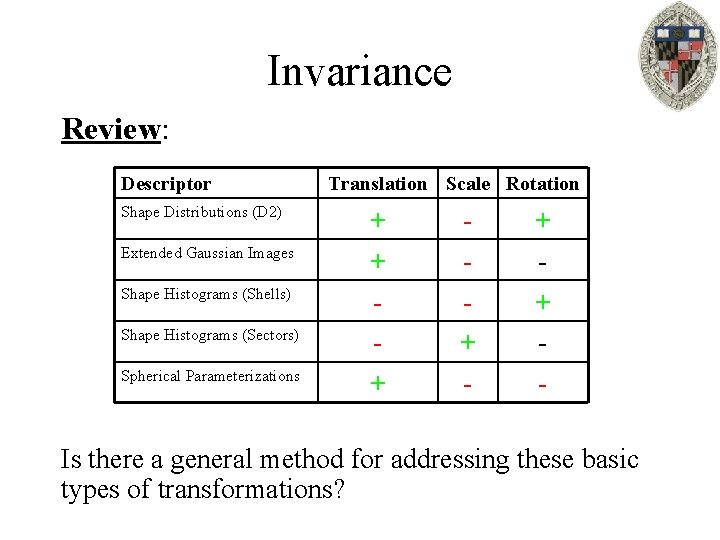
Invariance Review: Descriptor Shape Distributions (D 2) Extended Gaussian Images Shape Histograms (Shells) Shape Histograms (Sectors) Spherical Parameterizations Translation Scale Rotation + + - Is there a general method for addressing these basic types of transformations?

Invariance Properties: C C C D Can be computed in a pre-processing stage. Works for translation, scale and rotation. Gives a more compact representation. Tends to discard valuable, discriminating, information. ……. . . No Invariance ……. . ……Rotation …Translation + Rotation …………. …. . Rotation

Outline: • Challenge • General Approaches • Specific Examples – Normalization: PCA – Closed Form Solution: Ordered Point Sets

PCA Alignment Treat a surface as a collection of points and define the variance function:

PCA Alignment Define the covariance matrix M: Find the eigen-values and align so that the eigen-values map to the x-, y-, and z-axes

PCA Alignment Limitations: – Eigen-values are only defined up to sign! PCA alignment is only well-defined up to axial flips about the x-, y-, and z-axes.

PCA Alignment Limitations: –Assumes that the eigen-values are distinct and therefore the eigen-vectors are well-defined (up to sign). This is not always true and can make PCA alignment unstable.

Outline: • Challenge • General Approaches • Specific Examples – Normalization: PCA – Closed Form Solution: Ordered Point Sets

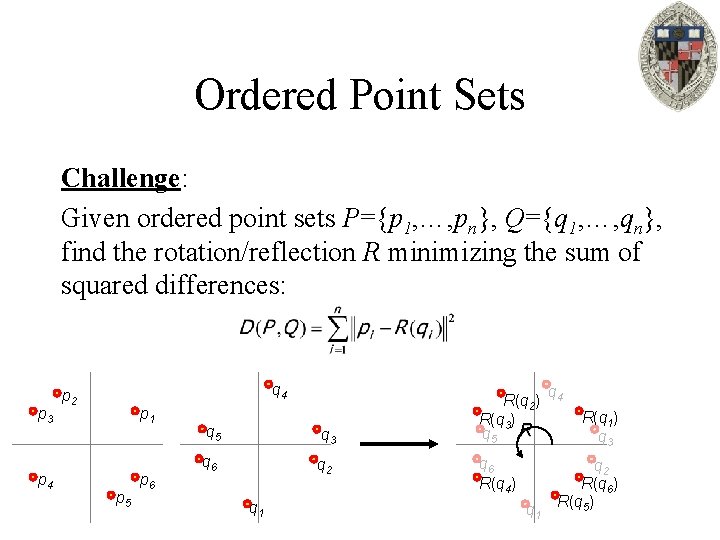
Ordered Point Sets Challenge: Given ordered point sets P={p 1, …, pn}, Q={q 1, …, qn}, find the rotation/reflection R minimizing the sum of squared differences: p 3 p 4 q 4 p 2 p 1 p 5 p 6 q 5 q 3 q 6 q 2 q 1 R(q 2) R(q 3) q 5 R q 6 R(q 4) q 1 q 4 R(q 1) q 3 q 2 R(q 6) R(q 5)

Review Vector dot-product: If v =(v 1, …, vn) and w=(w 1, …, wn) are two ndimensional vectors the dot-product of v with w is the sum of the product of the coefficients:

Review Trace: The trace of a nxn matrix M is the sum of the diagonal entries of M: Properties: – –

Review Trace: If M is any nxn matrix and D is a diagonal nxn matrix, then the trace of MD is the sum of the products of the diagonal entries. M D

Review Matrix multiplication: If M and N are two then the (i, j)th entry of the matrix MN is the dot-product of the jth row vector of M with the ith column vector of N. M jth row N ith column MN (i, j)th entry

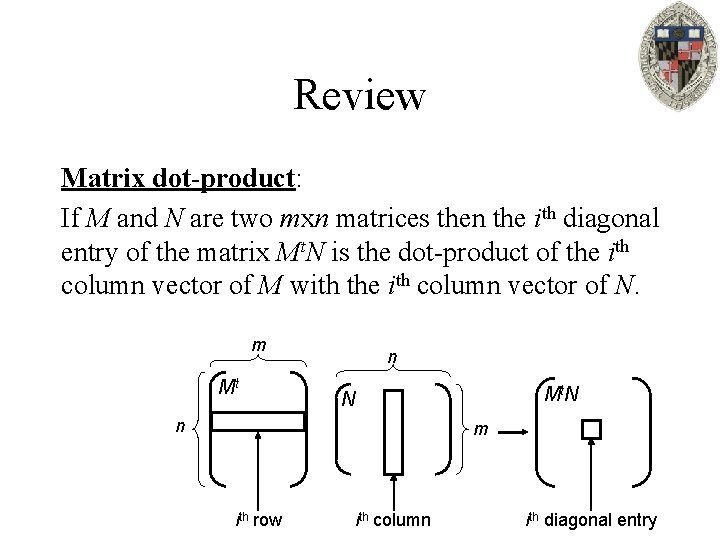
Review Matrix dot-product: If M and N are two mxn matrices then the ith diagonal entry of the matrix Mt. N is the dot-product of the ith column vector of M with the ith column vector of N. m Mt n Mt. N N n m ith row ith column ith diagonal entry

Review Matrix dot-product: We define the dot-product of two mxn matrices, M and N, to be the trace of the matrix product: (the sum of the dot-products of the column vectors).

Review SVD Factorization: If M is an mxm matrix, then M can be factored as the product: where D is a diagonal mxm matrix with non-negative entries and U and V are orthonormal (i. e. rotation/reflection) mxm matrices.

Trace Maximization Claim: If M is an mxm matrices, whose SVD factorization is: then the orthonormal transformation R=VUt is the orthonormal transformation maximizing the trace:

Trace Maximization Proof: We can rewrite the trace equation as: If we set R 0 to be the rotation R 0=Vt. RU, we get:

Trace Maximization Proof: Since R 0 is a rotation, each of its entries can have value no larger than one. Since D is diagonal, the value of the trace is the product of the diagonal elements of D and R 0.

Trace Maximization Proof: To maximize the trace we want R 0 to be maximal on the diagonal (i. e. have only 1’s). Thus, R 0 is the identity matrix and we have: So that the rotation/reflection R that maximizes Trace(RM) is:

Ordered Point Sets Challenge: Given ordered point sets P={p 1, …, pn}, Q={q 1, …, qn}, find the rotation/reflection R minimizing the sum of squared differences:

Ordered Point Sets Solution: Use the fact that we can express the difference: to rewrite the equation as:

Ordered Point Sets Solution: Use the fact that rotations preserves lengths: to rewrite the equation as:

Ordered Point Sets Solution: Since the value: Does not depend on the choice of rotation R, minimizing the sum of squared distances is equivalent to maximizing the sum of dot-products:

Ordered Point Sets Solution: If we let MP (respectively MQ) be the 3 xn matrix whose columns are the points pi (respectively qi) then we can rewrite the sum of the vector dot-products as the matrix dot product: and we can find the maximizing rotation/reflection R by trace maximization.