ALIGNMENT AND TOLERANCES David Boutin www cea fr

ALIGNMENT AND TOLERANCES David Boutin www. cea. fr 12 APRIL 2016, FCC WEEK, ROMA DECEMBER 19, 2021 CEA | 10 AVRIL 2012 | PAGE 1

OUTLINE Definition of the errors and correction scheme Evaluation of the results Dependency of various variables on the errors Conclusions and perspectives DECEMBER 19, 2021 D. BOUTIN, FCC WEEK, 12 APRIL 2016 | PAGE 2
ERROR DESCRIPTION FCC will be subject to various errors that will perturb its normal activity ⇒ important to have a correction scheme Two types of errors that contribute to beam misalignment are studied: position error and field error All errors are Gaussian distributed, truncated at 3 -σ values Position error is defined for all ‘MQ’ quadrupoles, present in arc and in dispersion suppression (DIS) regions: 0 < σδx < 0. 5 mm 0 < σδy < 0. 5 mm Field error (b 1) is defined for all ‘MB’ dipoles (in arcs) and ‘MBS’ dipoles (in DIS), in relative units: 0 < σδB/B < 0. 5 % No errors are applied in the insertion regions The error generator seed is user defined, and different for each of the 500 runs DECEMBER 19, 2021 D. BOUTIN, FCC WEEK, 12 APRIL 2016 | PAGE 3

CORRECTION SCHEME The complete FCC ring lattice is used All quadrupoles of the arcs and DIS sections have a BPM and a corrector (L = 0. 647 m) next to them, with the same polarity (BPMs are used on the corresponding plane only). Exception: the first quadrupole of the DIS before each arc section (no corrector), and the last quadrupole of the DIS after each arc section (no BPM). The errors are evaluated only for the arcs Same number of BPMs (parameters) and correctors (variables) Optimization using the CORRECT command of MADX (SVD mode) IR orbit correction done in parallel -> see talk of A. Seryi (next session) DECEMBER 19, 2021 D. BOUTIN, FCC WEEK, 12 APRIL 2016 | PAGE 4

EVALUATION OF THE RESULTS Evaluation of residual orbit, beta-beating Δβ/βref, parasitic dispersion or dispersion beating ΔD/√βref. → see LHC Project Report 501 for more details The RMS, values at 90% of the maximum (90 -percentile) are evaluated for all variables (only the 90% value is shown here) The dependency on each main error contribution is also studied: Quadrupole misalignment. The RMS error is assumed identical in both planes (x and y). Dipole field errors. The relative RMS error is assumed to be identical for the two types of magnets (MB and MBS). The reference errors of 0. 35 mm and 10 -3 for the quadrupole misalignment and dipole field errors are used when varying the other error contribution. DECEMBER 19, 2021 D. BOUTIN, FCC WEEK, 12 APRIL 2016 | PAGE 5
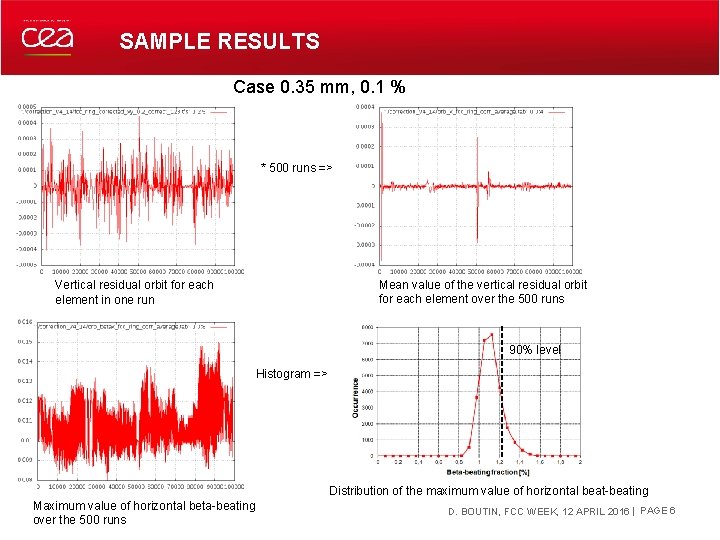
SAMPLE RESULTS Case 0. 35 mm, 0. 1 % * 500 runs => Mean value of the vertical residual orbit for each element over the 500 runs Vertical residual orbit for each element in one run 90% level Histogram => Distribution of the maximum value of horizontal beat-beating Maximum value horizontal beta-beating DECEMBER 19, of 2021 over the 500 runs D. BOUTIN, FCC WEEK, 12 APRIL 2016 | PAGE 6
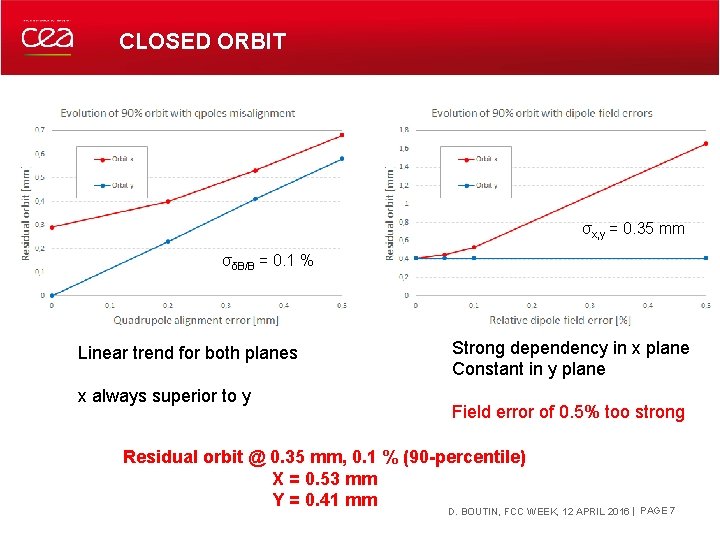
CLOSED ORBIT σx, y = 0. 35 mm σδB/B = 0. 1 % Linear trend for both planes x always superior to y Strong dependency in x plane Constant in y plane Field error of 0. 5% too strong Residual orbit @ 0. 35 mm, 0. 1 % (90 -percentile) X = 0. 53 mm Y = 0. 41 mm DECEMBER 19, 2021 D. BOUTIN, FCC WEEK, 12 APRIL 2016 | PAGE 7
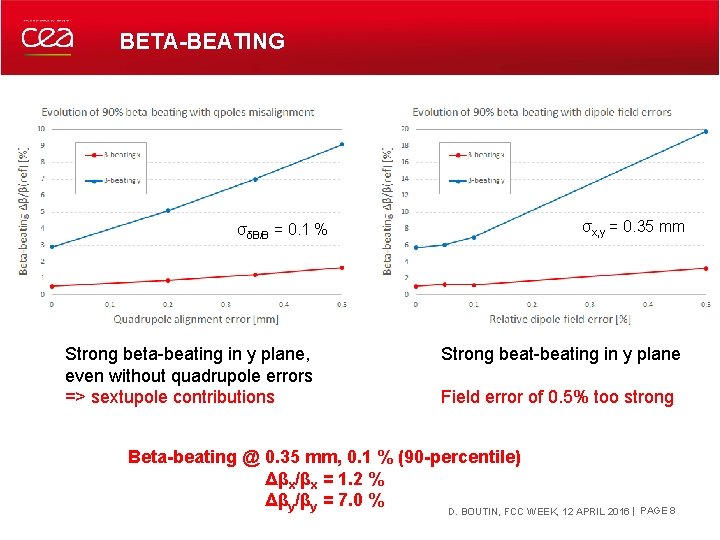
BETA-BEATING σδB/B = 0. 1 % Strong beta-beating in y plane, even without quadrupole errors => sextupole contributions σx, y = 0. 35 mm Strong beat-beating in y plane Field error of 0. 5% too strong Beta-beating @ 0. 35 mm, 0. 1 % (90 -percentile) Δβx/βx = 1. 2 % Δβy/βy = 7. 0 % DECEMBER 19, 2021 D. BOUTIN, FCC WEEK, 12 APRIL 2016 | PAGE 8
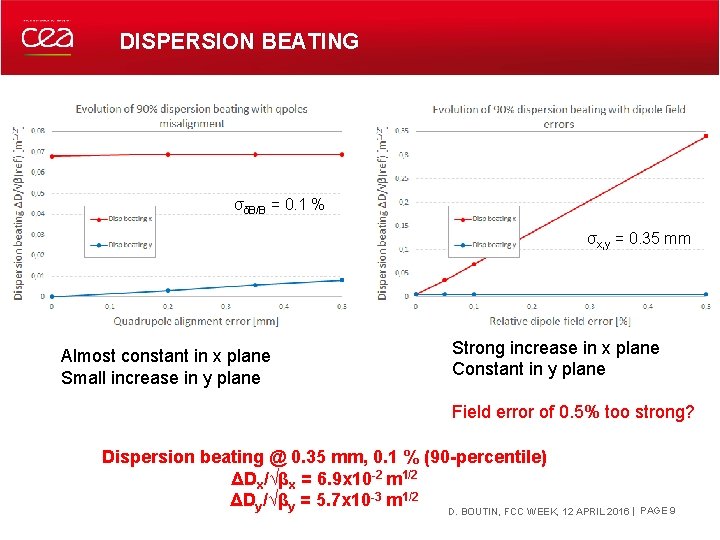
DISPERSION BEATING σδB/B = 0. 1 % σx, y = 0. 35 mm Almost constant in x plane Small increase in y plane Strong increase in x plane Constant in y plane Field error of 0. 5% too strong? Dispersion beating @ 0. 35 mm, 0. 1 % (90 -percentile) ΔDx/√βx = 6. 9 x 10 -2 m 1/2 ΔDy/√βy = 5. 7 x 10 -3 m 1/2 DECEMBER 19, 2021 D. BOUTIN, FCC WEEK, 12 APRIL 2016 | PAGE 9
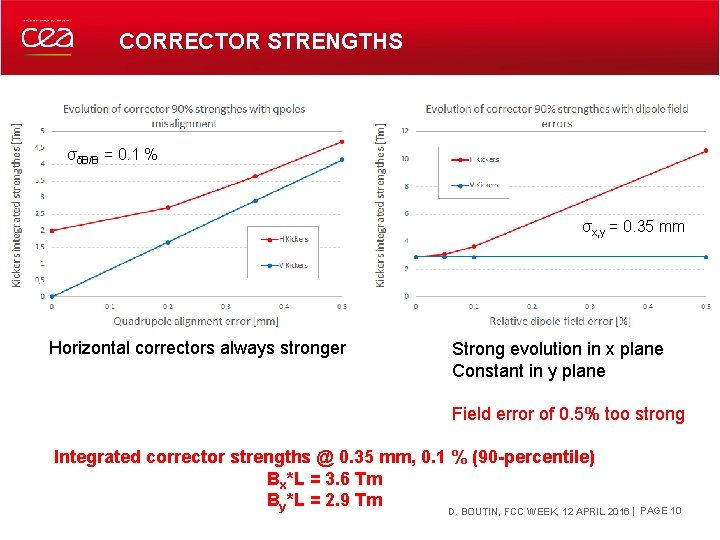
CORRECTOR STRENGTHS σδB/B = 0. 1 % σx, y = 0. 35 mm Horizontal correctors always stronger Strong evolution in x plane Constant in y plane Field error of 0. 5% too strong Integrated corrector strengths @ 0. 35 mm, 0. 1 % (90 -percentile) Bx*L = 3. 6 Tm By*L = 2. 9 Tm DECEMBER 19, 2021 D. BOUTIN, FCC WEEK, 12 APRIL 2016 | PAGE 10
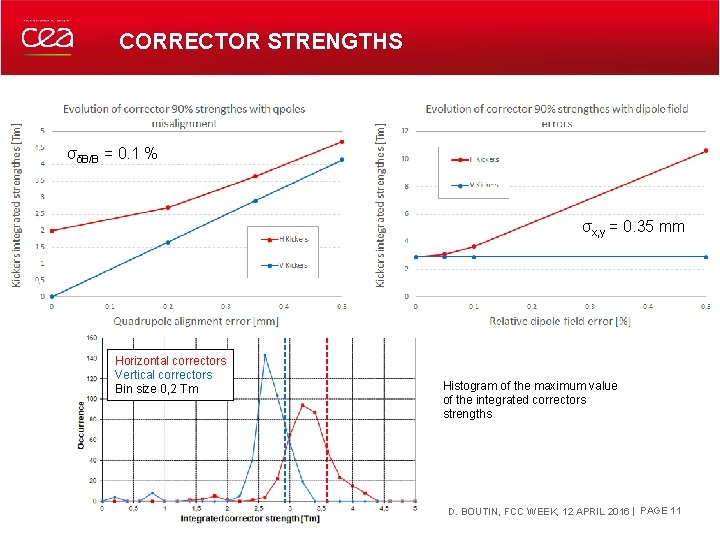
CORRECTOR STRENGTHS σδB/B = 0. 1 % σx, y = 0. 35 mm Horizontal correctors Vertical correctors Bin size 0, 2 Tm DECEMBER 19, 2021 Histogram of the maximum value of the integrated correctors strengths D. BOUTIN, FCC WEEK, 12 APRIL 2016 | PAGE 11

CONCLUSIONS AND PERSPECTIVES Corrections of the closed orbit have been performed in all arcs of the FCC ring For a configuration with 0. 35 mm quadrupoles alignment errors and dipole relative field errors of 10 -3 the correctors have an integrated strength up to +/- 3. 6 Tm @ 90 -percentile level Dependency on input errors has been studied for several variables The case of dipole errors of 0. 5 % and above can be excluded To be done: Test more errors combinations (different for MB and MBS, different in x and y for quadrupoles, roll angle plus field error in the dipoles) Test ‘clustering’ of errors (as the alignment of a group of magnets is done in real world) Compare with different matching methods (LMDIF, . . ) Use a different correction scheme (remove 1/n correctors/BPMs) Comparison with LHC scheme DECEMBER 19, 2021 D. BOUTIN, FCC WEEK, 12 APRIL 2016 | PAGE 12
- Slides: 12