Algumas classes especiais de grafo Teoria dos Grafos

Algumas classes especiais de grafo Teoria dos Grafos UFES

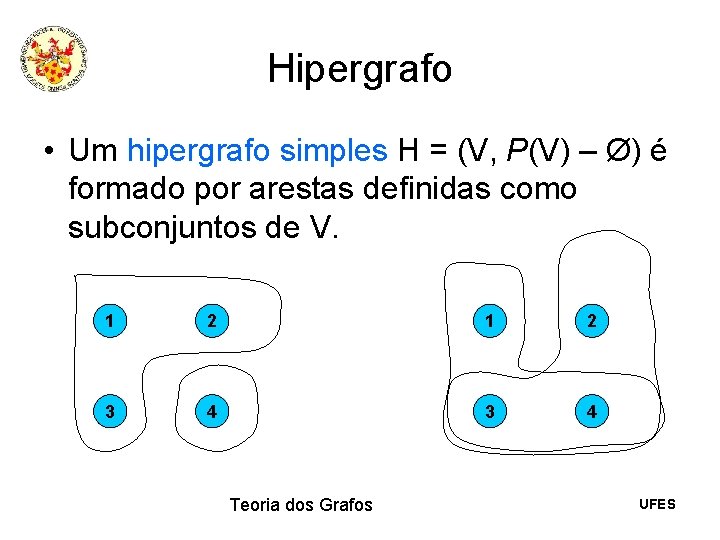
Hipergrafo • Um hipergrafo simples H = (V, P(V) – Ø) é formado por arestas definidas como subconjuntos de V. 1 2 3 4 Teoria dos Grafos UFES

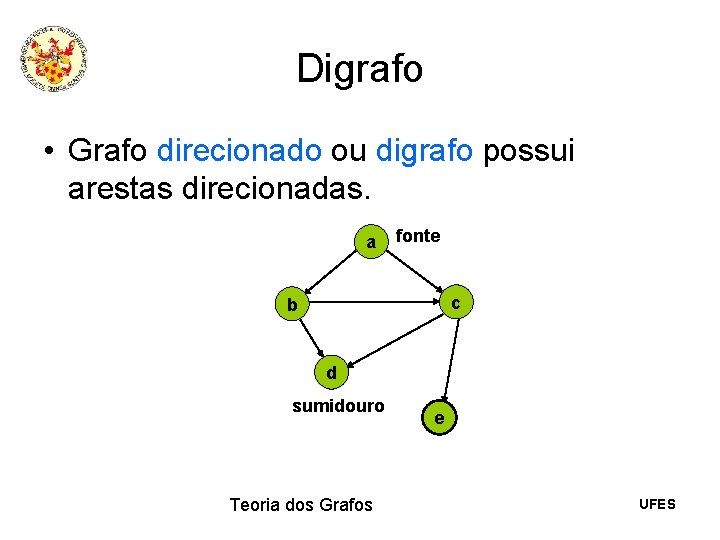
Digrafo • Grafo direcionado ou digrafo possui arestas direcionadas. a fonte c b d sumidouro Teoria dos Grafos e UFES

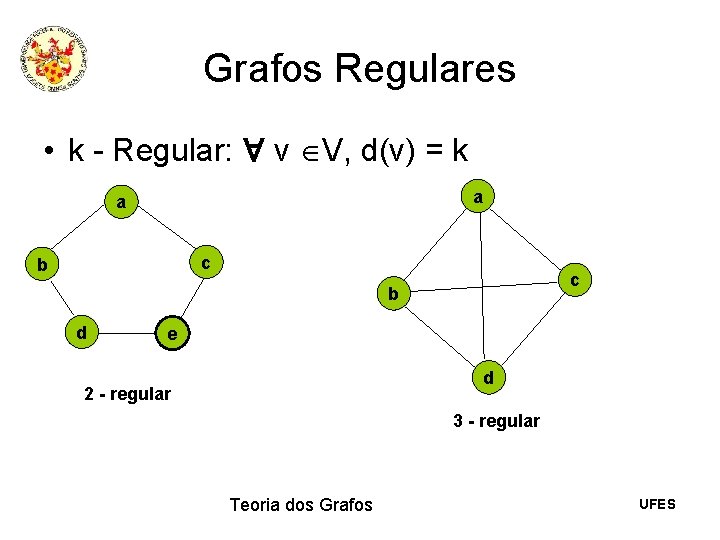
Grafos Regulares • k - Regular: v V, d(v) = k a a c b d e d 2 - regular 3 - regular Teoria dos Grafos UFES

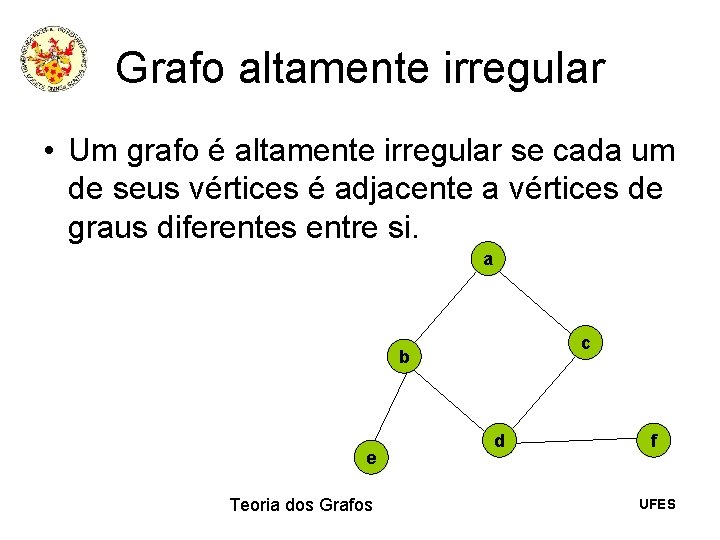
Grafo altamente irregular • Um grafo é altamente irregular se cada um de seus vértices é adjacente a vértices de graus diferentes entre si. a c b e Teoria dos Grafos d f UFES

Grafo Nulo ou Trivial • Um grafo G = (V, E) é dito nulo se V ≠ Ø e E=Ø – Um grafo deve ter pelo menos um vértice. a c b d Teoria dos Grafos e UFES

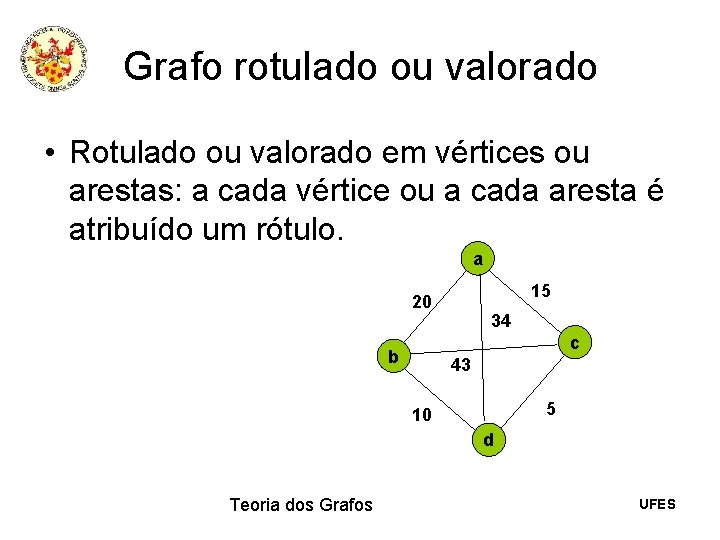
Grafo rotulado ou valorado • Rotulado ou valorado em vértices ou arestas: a cada vértice ou a cada aresta é atribuído um rótulo. a 15 20 34 c b 43 5 10 d Teoria dos Grafos UFES

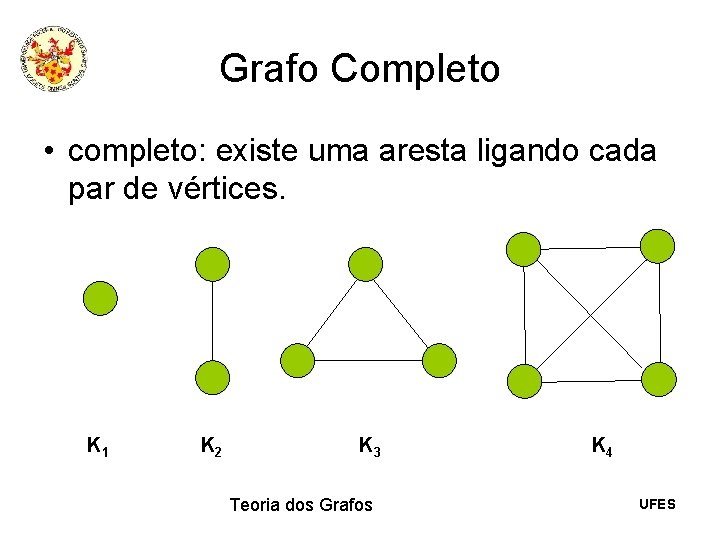
Grafo Completo • completo: existe uma aresta ligando cada par de vértices. K 1 K 2 K 3 Teoria dos Grafos K 4 UFES

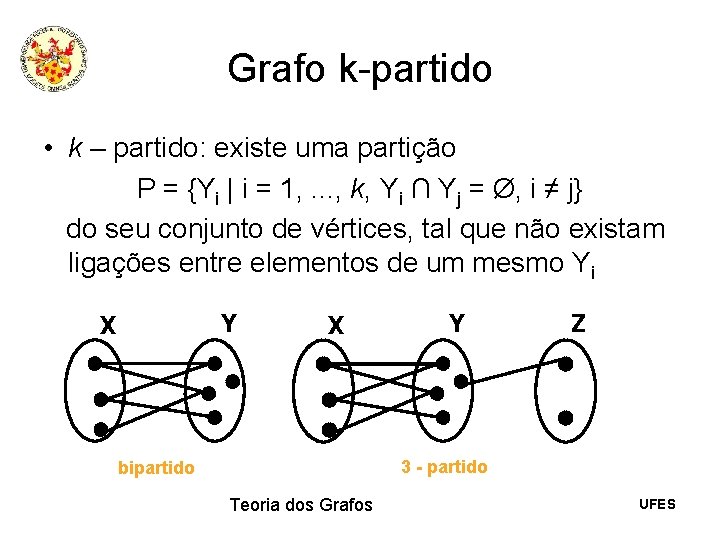
Grafo k-partido • k – partido: existe uma partição P = {Yi | i = 1, . . . , k, Yi ∩ Yj = Ø, i ≠ j} do seu conjunto de vértices, tal que não existam ligações entre elementos de um mesmo Yi Y X X Y Z 3 - partido bipartido Teoria dos Grafos UFES

Grafo Bipartido Completo • é um grafo bipartido com bipartição (X, Y) em que cada vértice de X é adjacente a cada vértice de Y. – Se |X|=p e |Y|=q, então denotamos tal grafo por Kp, q q Teoria dos Grafos UFES

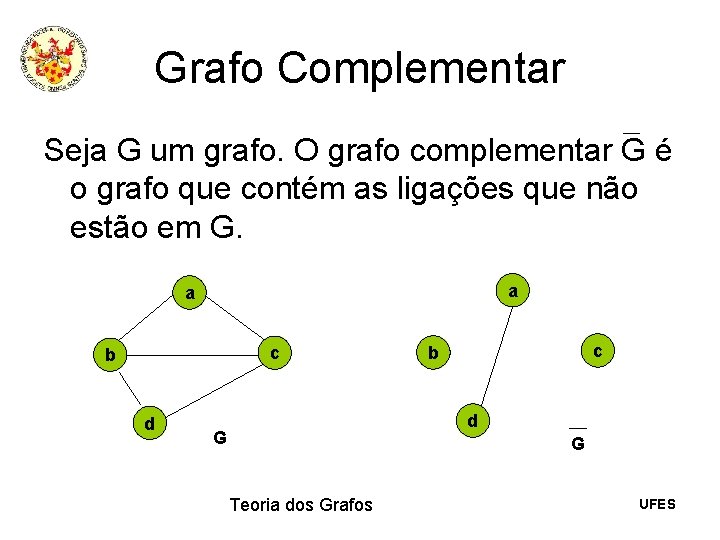
Grafo Complementar Seja G um grafo. O grafo complementar G é o grafo que contém as ligações que não estão em G. a a c b d G G Teoria dos Grafos UFES

Subgrafos Teoria dos Grafos UFES

Subgrafos • Um grafo H é um subgrafo de G (H G) se V(H) V(G) e E(H) E(G) • Quando H G e H G, denotamos H G e dizemos que H é subgrafo próprio de G • Se H é um subgrafo de G então G é um supergrafo de H • Um subgrafo gerador de G é um subgrafo H com V(H) = V(G) Teoria dos Grafos UFES

Subgrafo Induzido (por vértice) • Seja V´ um subconjunto não vazio de V. O subgrafo de G cujo conjunto de vértices é V´ e o conjunto de arestas é o conjunto de todas as arestas de G com ambos extremos em V´ é chamado de subgrafo de G induzido por V'. • G[V’]: é um subgrafo induzido de G por V´. Teoria dos Grafos UFES

Subgrafo induzido (por aresta) • Seja E´um subconjunto não vazio de arestas de E. O subgrafo de G cujo conjunto de vértices é o conjunto dos extremos das arestas em E´ é chamado de subgrafo de G induzido por arestas Teoria dos Grafos UFES

G[VV´] denotado por G-V’ • É o subgrafo obtido a partir de G pela remoção dos vértices em V´ e suas arestas incidentes • Se V´={v}, escrevemos G-v ao invés de G{v} Teoria dos Grafos UFES

G – E' e G + E' • G-E´: subgrafo gerador de G com conjunto de arestas EE´ • G+E´: grafo obtido a partir de G adicionando um conjunto de arestas E´ Teoria dos Grafos UFES

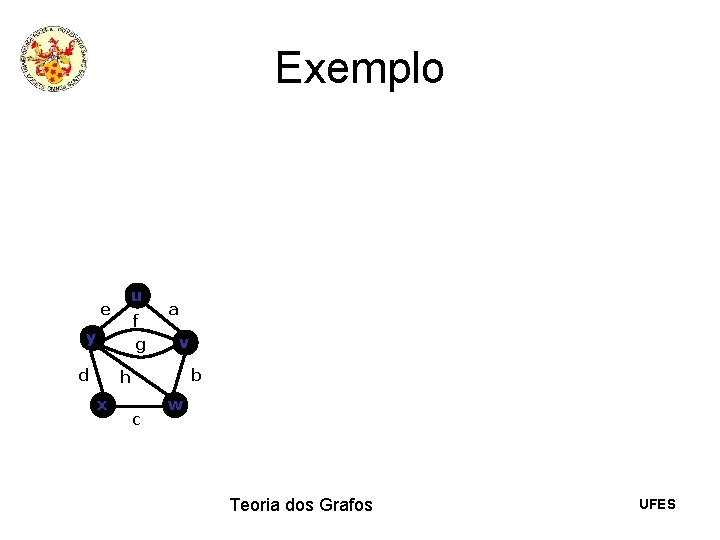
Exemplo u e f g y d a v b h x c w Teoria dos Grafos UFES

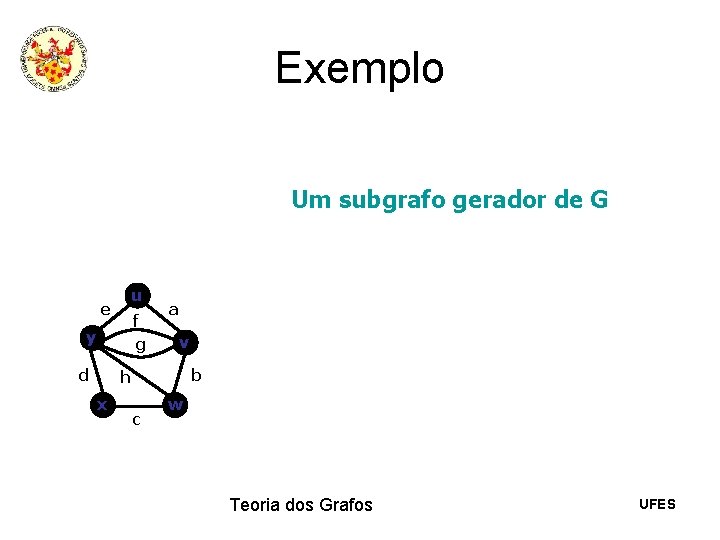
Exemplo Um subgrafo gerador de G u e f g y d a v b h x c w Teoria dos Grafos UFES

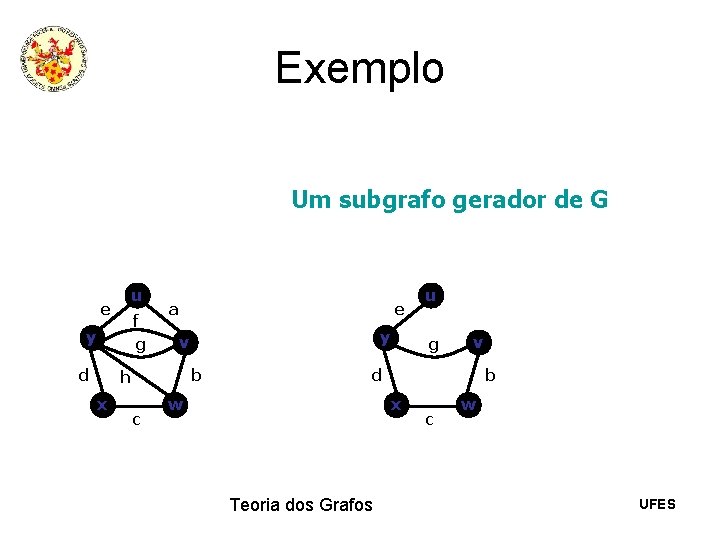
Exemplo Um subgrafo gerador de G u e f g y d a e b h x y v c u g v d w b x Teoria dos Grafos c w UFES

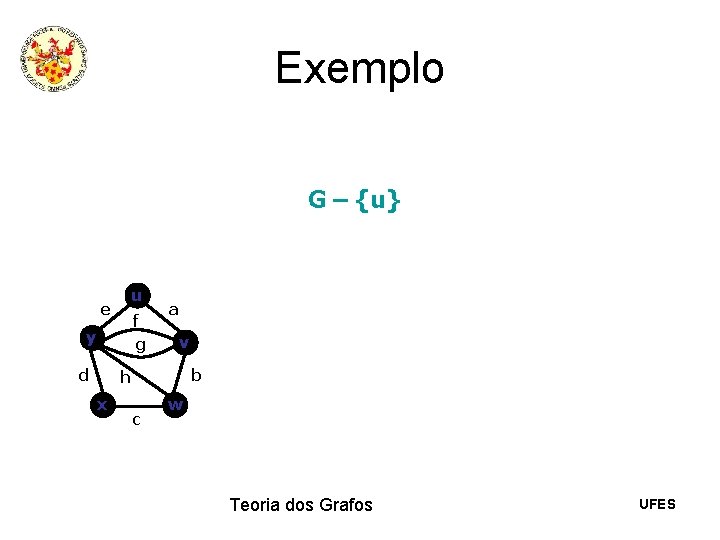
Exemplo G – {u} u e f g y d a v b h x c w Teoria dos Grafos UFES

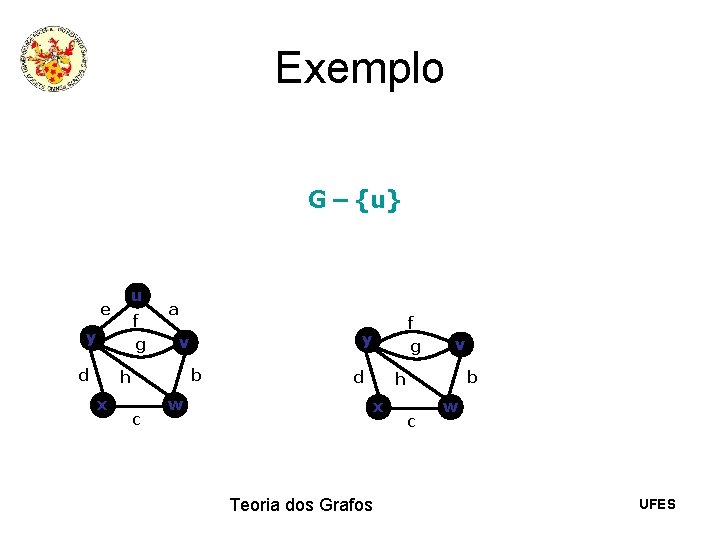
Exemplo G – {u} u e f g y d a x y v b h c w f g d v b h x Teoria dos Grafos c w UFES

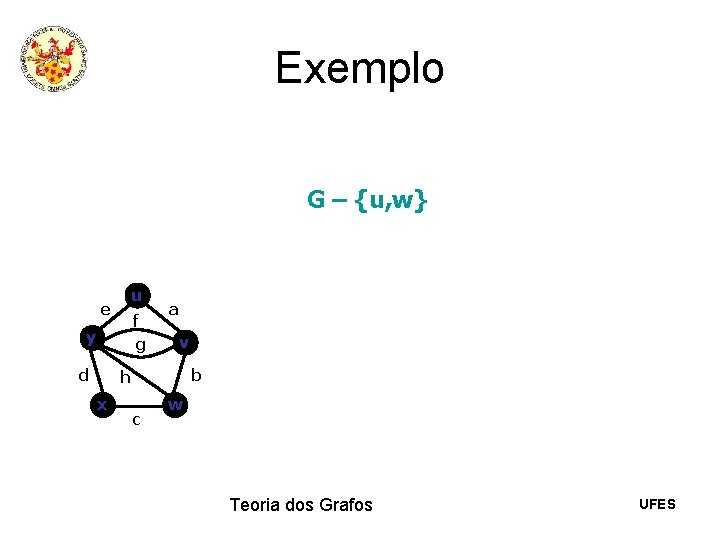
Exemplo G – {u, w} u e f g y d a v b h x c w Teoria dos Grafos UFES

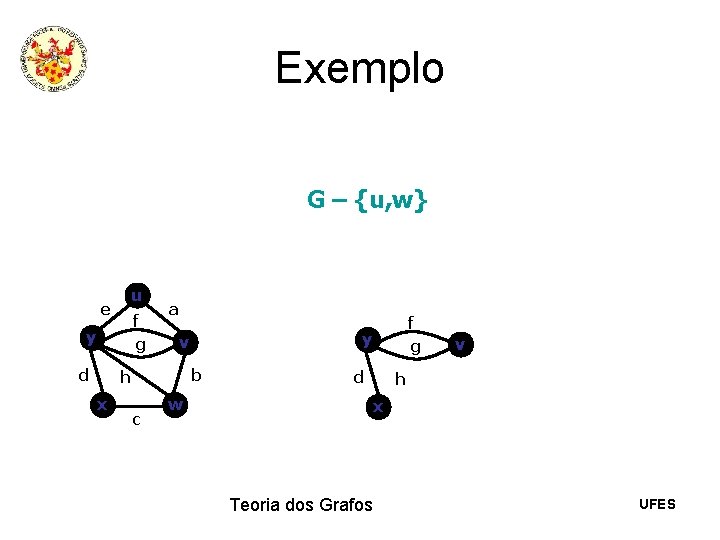
Exemplo G – {u, w} u e f g y d a x y v b h c w f g d v h x Teoria dos Grafos UFES

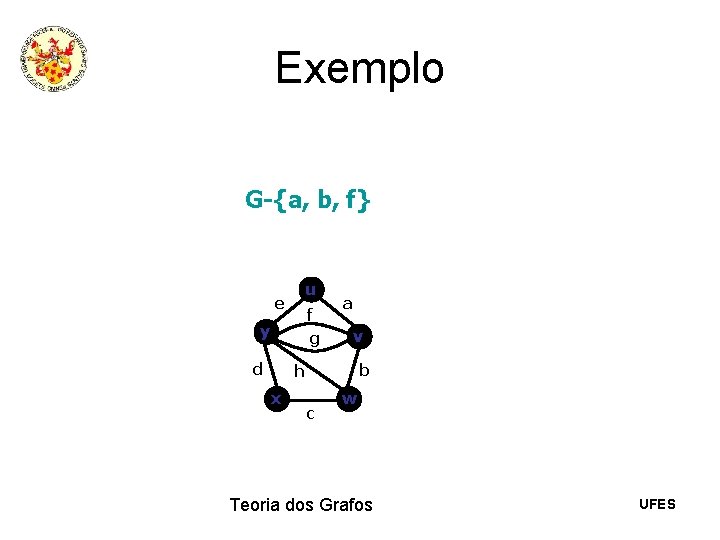
Exemplo G-{a, b, f} u e f g y d a v b h x c w Teoria dos Grafos UFES

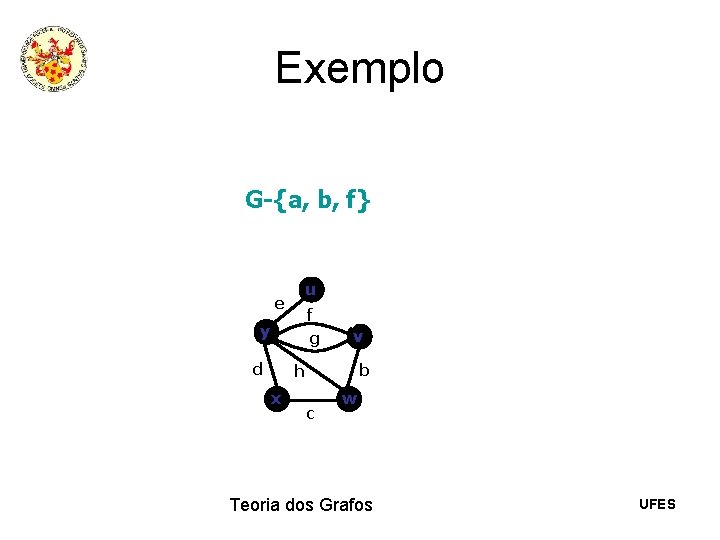
Exemplo G-{a, b, f} u e f g y d v b h x c w Teoria dos Grafos UFES

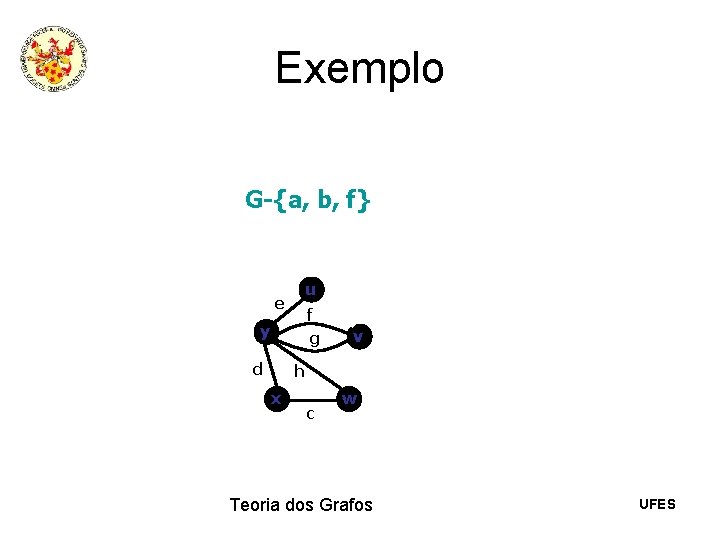
Exemplo G-{a, b, f} u e f g y d v h x c w Teoria dos Grafos UFES

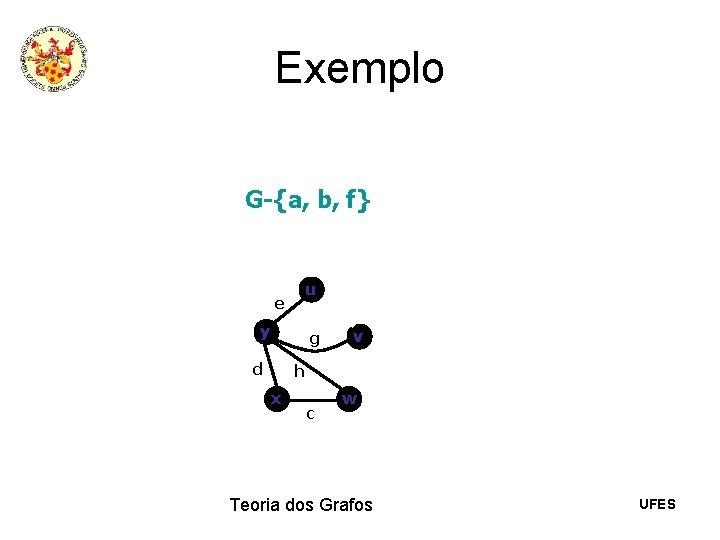
Exemplo G-{a, b, f} u e y g d v h x c w Teoria dos Grafos UFES

Exemplo O subgrafo induzido G[u, v, x] u e f g y d a v b h x c w Teoria dos Grafos UFES

Exemplo O subgrafo induzido G[u, v, x] u e f g y d u a v b h x v c w x Teoria dos Grafos UFES

Exemplo O subgrafo induzido G[u, v, x] u e f g y d u a v b h x v c w x Teoria dos Grafos UFES

Exemplo O subgrafo induzido G[a, d, e, g] por aresta u e f g y d a v b h x c w Teoria dos Grafos UFES

Exemplo O subgrafo induzido G[a, d, e, g] por aresta u e f g y d a e b h x y v c w u g a v d x Teoria dos Grafos UFES

Subgrafos Disjuntos • Sejam G 1, G 2 G G 1 e G 2 são disjuntos (em vértices) se V(G 1) V(G 2) = Teoria dos Grafos UFES

Subgrafos Disjuntos em aresta • Sejam G 1, G 2 G G 1 e G 2 são disjuntos em aresta se E(G 1) E(G 2) = Teoria dos Grafos UFES

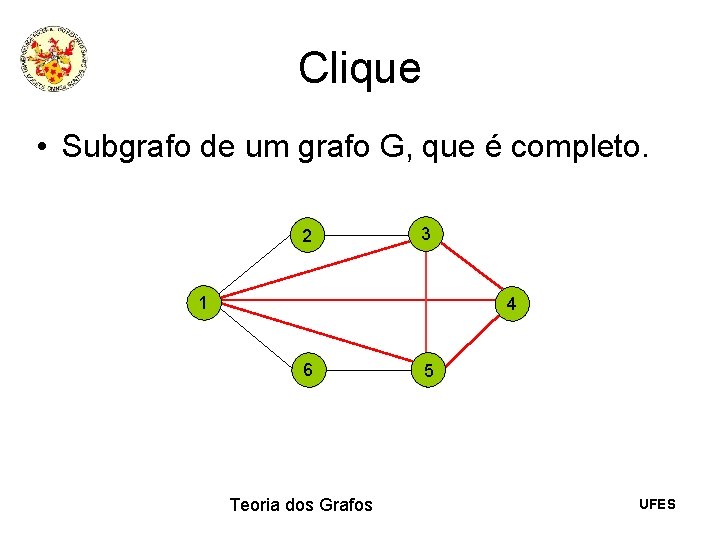
Clique • Subgrafo de um grafo G, que é completo. 2 3 1 4 6 Teoria dos Grafos 5 UFES

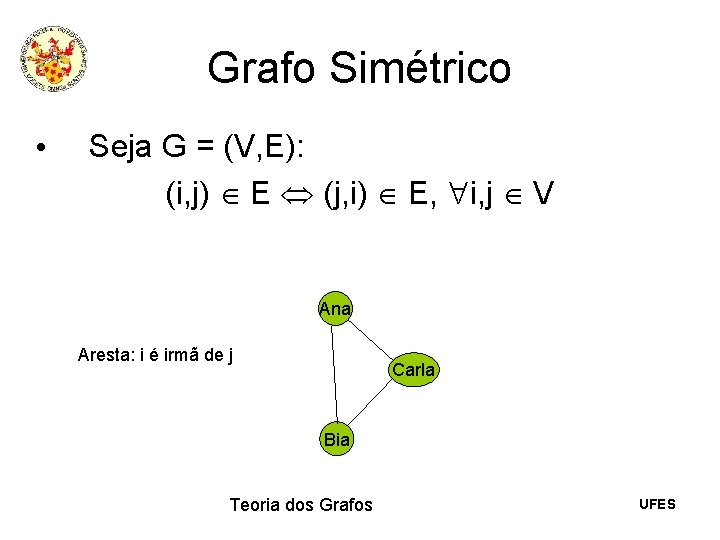
Grafo Simétrico • Seja G = (V, E): (i, j) E (j, i) E, i, j V Ana Aresta: i é irmã de j Carla Bia Teoria dos Grafos UFES

Grafo Anti-simétrico • Seja G = (V, E): (i, j) E (j, i) E • Essa característica não se aplica a grafos não orientados Teoria dos Grafos UFES

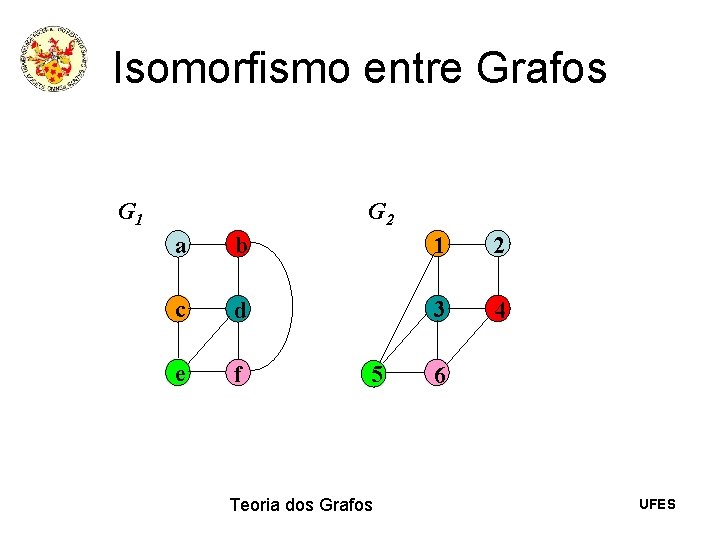
Isomorfismo entre Grafos • Um isomorfismo entre dois grafos é uma bijeção f de V(G) em V(H) tal que {u, v} E(G) {f(u), f(v)} E(H) • É possível alterar o nome dos vértices de um deles de forma que fiquem iguais. Teoria dos Grafos UFES

Isomorfismo entre Grafos G 2 G 1 a b 1 2 c d 3 4 e f 5 Teoria dos Grafos 6 UFES

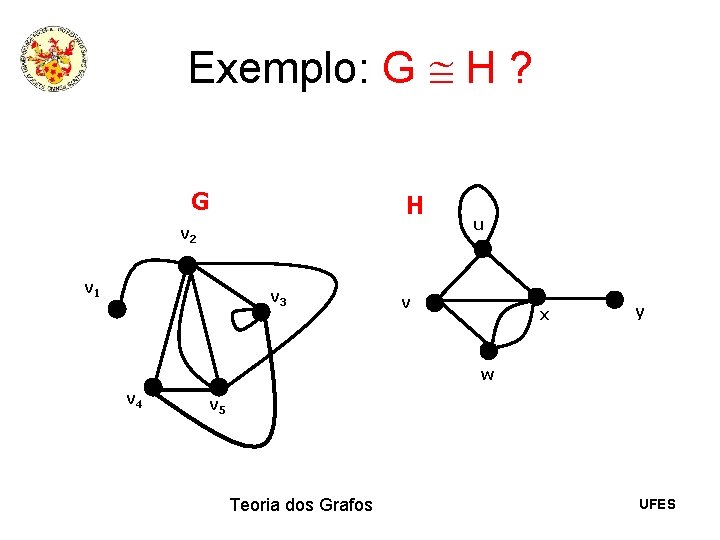
Exemplo: G H ? G H v 2 v 1 v 3 u v x y w v 4 v 5 Teoria dos Grafos UFES

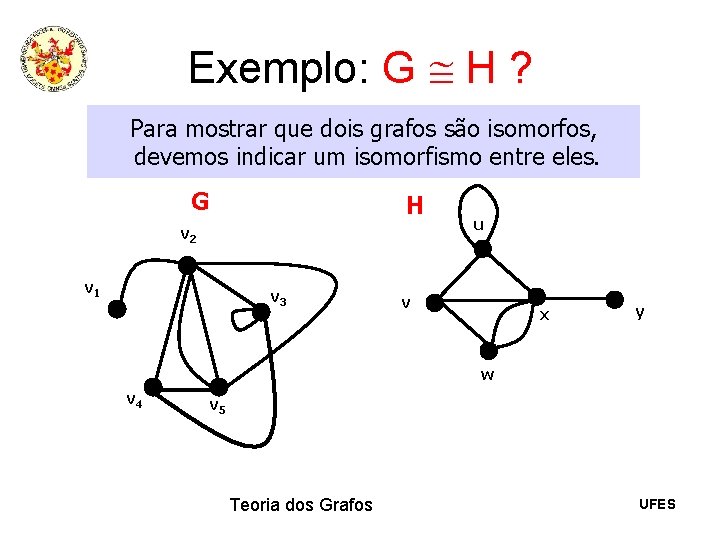
Exemplo: G H ? Para mostrar que dois grafos são isomorfos, devemos indicar um isomorfismo entre eles. G H v 2 v 1 v 3 u v x y w v 4 v 5 Teoria dos Grafos UFES

Isomorfismo de subgrafos • Dados dois grafos G 1 = (V 1, E 1) e G 2 = (V 2, E 2), diz-se que G 1 contém um subgrafo isomorfo a G 2 sss existem um subconjunto V V 1 e um subconjunto E E 1 tal que |V| = |V 2| e |E| = |E 2| e uma função biunívoca f: V 2 → V tal que {u, v} E 2 sss {f(u), f(v)} E Teoria dos Grafos UFES

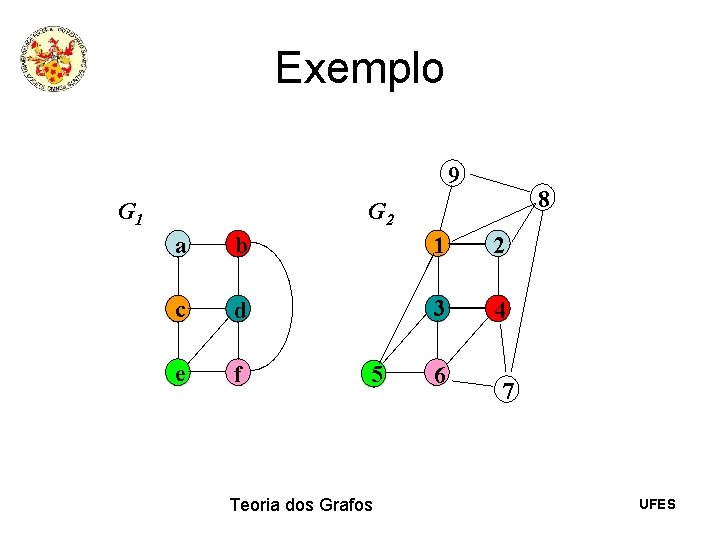
Exemplo 9 G 1 8 G 2 a b 1 2 c d 3 4 e f 5 Teoria dos Grafos 6 7 UFES

Exercícios Teoria dos Grafos UFES

• Os turistas John, Leuzinger, Dufois e Medeiros se encontram em um bar em Paris e começam a conversar. As línguas disponíveis são o inglês, o francês, o português e o alemão. John fala todas as línguas, Leuzinger não fala o português, Dufois fala francês e alemão e Medeiros fala inglês e português. – Represente por meio de um hipergrafo H = (V, W) as capacidades linguísticas do grupo. Qual é o significado das interseções Wi Wj, onde Wk W? Teoria dos Grafos UFES

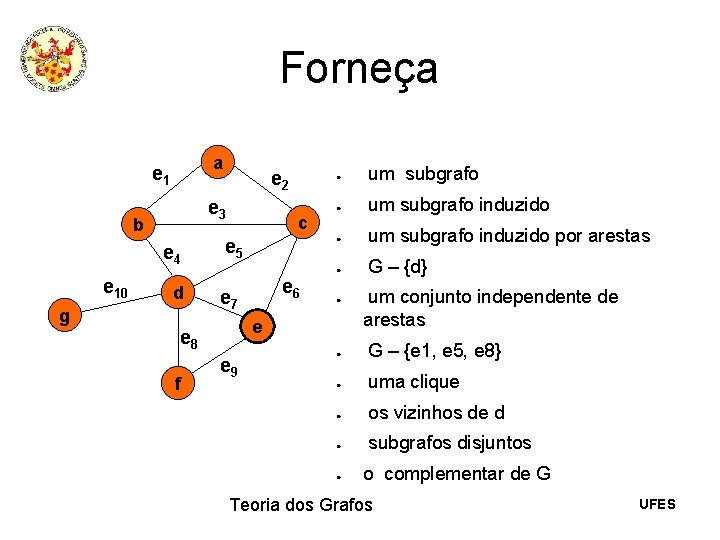
Forneça a e 1 e 3 b e 4 e 10 e 2 d g c e 5 um subgrafo induzido por arestas G – {d} e e 8 f e 6 e 7 e 9 um conjunto independente de arestas G – {e 1, e 5, e 8} uma clique os vizinhos de d subgrafos disjuntos o complementar de G Teoria dos Grafos UFES

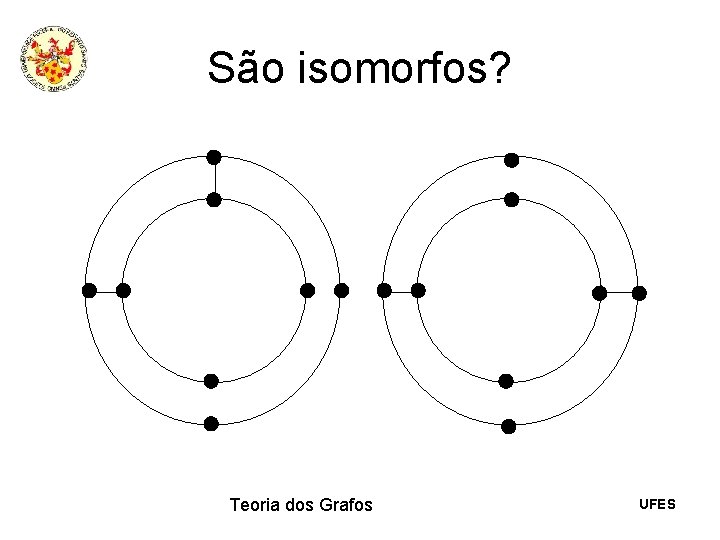
São isomorfos? Teoria dos Grafos UFES

• Mostre que não existem grafos k-regulares com k ímpar que possuam um número ímpar de vértices • Mostre que não existem grafos de 10 vértices e 24 arestas com d(v) {1, 5} v de V. Teoria dos Grafos UFES

Descreva o grafo que representa a situação a seguir ou mostre ser impossível descrevê-lo: cada um de 102 estudantes serão associados a 1 de 35 computadores e cada um dos 35 computadores serão usados exatamente por 1 ou 3 estudantes. Teoria dos Grafos UFES