Algoritmul lui Dijkstra Este un algoritm care calculeaza

Algoritmul lui Dijkstra Este un algoritm care calculeaza drumurile minime de la un nod al unui graf la toate celelalte noduri din graf Grafurile pe care poate lucra algoritmul lui Dijkstra sunt, in general, ponderate si orientate – arcele sunt orientate de la un nod la alt nod (nu se poate merge si invers) si au un anumit cost de care se va tine seama in aflarea drumului minim Calin Jebelean Algoritmul lui Dijkstra 1

Algoritmul lui Dijkstra Daca graful este neponderat (arcele nu au costuri asociate) atunci drum minim intre doua noduri se considera drumul alcatuit din numar minim de arce Pentru a gasi drumul minim de la un nod X la un nod Y se poate aplica o cautare prin cuprindere pornind de la nodul X – prima aparitie a lui Y in coada algoritmului de cautare prin cuprindere presupune existenta unui drum cu numar minim de arce de la X la Y, care poate fi reconstituit Pe un astfel de graf se poate aplica si algoritmul lui Dijkstra, daca transformam in prealabil graful intr-unul ponderat, asociind fiecarui arc acelasi cost (de exemplu, costul 1) Drumul de cost minim intre doua noduri obtinut in urma aplicarii algoritmului Dijkstra va avea si numar minim de arce din moment ce toate arcele au acelasi cost Calin Jebelean Algoritmul lui Dijkstra 2

Algoritmul lui Dijkstra functioneaza atat pe grafuri conexe cat si pe grafuri neconexe Un graf este conex daca din orice nod al sau se poate ajunge in orice alt nod In cazul grafurilor orientate, pentru ca intre doua noduri sa existe un drum in graf, nu este suficient sa existe o succesiune de arce intre cele doua noduri, ci arcele trebuie sa fie si orientate in sensul corespunzator Un drum intr-un graf orientat trebuie sa parcurga numai arce orientate identic, de la nodul sursa pana la nodul destinatie Daca nu exista nici un drum de la nodul de start la un alt nod al grafului atunci algoritmul lui Dijkstra va raporta existenta unui drum de lungime infinita intre ele – acest rezultat indica, de fapt, lipsa oricarui drum intre cele doua noduri Calin Jebelean Algoritmul lui Dijkstra 3

Algoritmul lui Dijkstra Intrare: n n Algoritmul porneste de la un graf orientat si ponderat cu N noduri De asemenea, e nevoie de un nod de start apartinand grafului – acesta este nodul de la care se doreste aflarea drumurilor minime pana la celelalte noduri din graf Iesire: n n Rezultatul algoritmului se prezinta sub forma unui tablou D cu N intrari, continand distantele minime de la nodul de start la toate celelalte noduri din graf De asemenea, tot ca rezultat se poate obtine si arborele drumurilor minime (in cazul in care ne intereseaza nu numai lungimile minime ale drumurilor, ci si drumurile propriu-zise) – acesta este un arbore generalizat care se va obtine sub forma unui tablou T cu N intrari (implementarea cu indicatori spre parinte) Calin Jebelean Algoritmul lui Dijkstra 4

Algoritmul lui Dijkstra Fie X nodul de start – acesta se marcheaza ca vizitat Ideea gasirii drumului minim de la X la un un alt nod este cautarea treptata: se presupune ca drumul minim este alcatuit dintr-un singur arc (arcul direct intre X si nodul tinta, care poate sa nu existe, costul sau fiind infinit in acest caz), apoi se cauta drumuri mai scurte alcatuite din 2 arce, apoi din 3, etc. – un drum minim nu poate avea mai mult de N-1 arce, deci algoritmul are N-1 pasi (al N-lea este banal) Dupa pasul k (1 ≤ k ≤ N-1), tabloul D va contine lungimile drumurilor minime de la nodul X la celelalte noduri, toate aceste drumuri fiind alcatuite din maxim k arce Astfel, D[Y] = L dupa pasul k inseamna ca de la X la Y exista un drum minim de lungime L alcatuit din maxim k arce Deci, dupa pasul k, au fost gasite numai drumurile minime alcatuite din maxim k arce – abia la finalul algoritmului (dupa pasul N-1) drumurile minime obtinute sunt definitive, ele fiind drumuri minime alcatuite din maxim N-1 arce Calin Jebelean Algoritmul lui Dijkstra 5

Algoritmul lui Dijkstra La inceputul fiecarui pas k avem un set de k-1 noduri marcate (in cadrul pasilor precedenti) – nodurile marcate sunt cele pentru care se cunoaste drumul minim (initial, doar nodul de start este marcat deoarece doar pentru el se cunoaste drumul minim) In cadrul pasului k trebuie executate 3 operatiuni: n Se gaseste acel nod Y nemarcat care D[Y] minim (acesta este singurul dintre nodurile nemarcate pentru care se poate spune sigur ca drumul minim are lungimea D[Y]) – pentru celelalte noduri nemarcate valoarea corespunzatoare din tabloul D s-ar putea sa nu reprezinte lungimea drumului minim ci un drum minim intermediar (alcatuit din maxim k-1 arce) care poate fi imbunatatit in cadrul pasilor viitori ai algoritmului n Nodul Y se marcheaza ca vizitat n Pentru fiecare nod Z ramas nemarcat se executa urmatorul algoritm: if D[Z] > D[Y] + Arc(Y , Z) then begin D[Z] : = D[Y] + Arc(Y , Z); T[Z] : = Y end Calin Jebelean Algoritmul lui Dijkstra 6

Algoritmul lui Dijkstra Logica este urmatoarea: D[Y] contine lungimea drumului minim de la nodul de start la nodul Y care trece numai prin noduri marcate (Y fiind, la inceputul pasului k, nodul nemarcat care avea D[Y] minim) – acest drum este alcatuit din maxim k-1 arce – D[Y] fiind minim, il marcam pe Y deoarece nu poate exista un drum mai scurt de la X la Y D[Z] contine lungimea celui mai scurt drum de la nodul de start la nodul Z alcatuit din maxim k-1 arce – acest drum trece doar prin noduri marcate, fara sa tina cont ca, intre timp, si Y a fost marcat S-ar putea sa existe un drum mai scurt decat D[Z] de la nodul de start la Z alcatuit din maxim k arce care trece numai prin noduri marcate, inclusiv nodul Y – unicul drum cu aceasta proprietate care poate fi mai scurt decat D[Z] este cel care include drumul minim pana la Y si arcul direct intre Y si Z, deci lungimea sa este D[Y] + Arc(Y , Z) Calin Jebelean Algoritmul lui Dijkstra 7

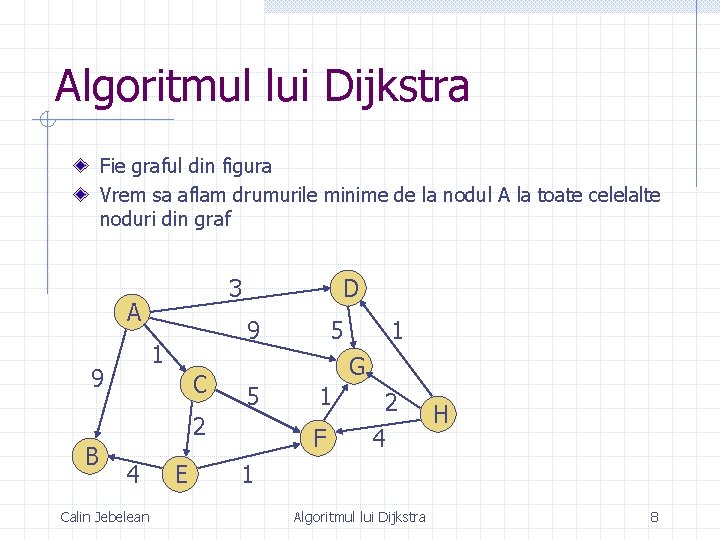
Algoritmul lui Dijkstra Fie graful din figura Vrem sa aflam drumurile minime de la nodul A la toate celelalte noduri din graf 3 A 9 1 9 D C 4 Calin Jebelean E 1 G 5 2 B 5 1 F 2 4 H 1 Algoritmul lui Dijkstra 8

Algoritmul lui Dijkstra Algoritmul trebuie sa returneze urmatorul rezultat: D= T= - 7 1 3 3 4 5 ∞ A E A A C E F A B C D E F G H Tabloul D are cate o intrare pentru fiecare nod al grafului, corespunzand lungimii drumului minim de la nodul A pana la respectivul nod Astfel, drumul minim de la A nu intereseaza (-), drumul minim de la A la F are lungimea 4, drumul minim de la A la H nu exista (∞), etc. Calin Jebelean Algoritmul lui Dijkstra 9

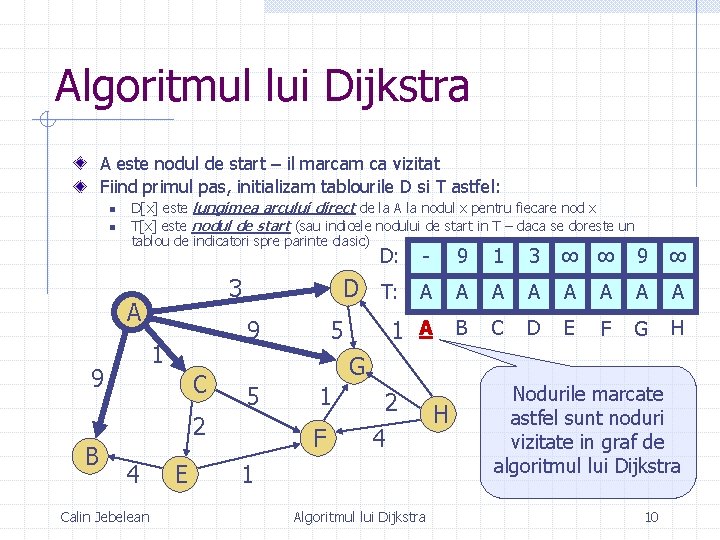
Algoritmul lui Dijkstra A este nodul de start – il marcam ca vizitat Fiind primul pas, initializam tablourile D si T astfel: n n D[x] este lungimea arcului direct de la A la nodul x pentru fiecare nod x T[x] este nodul de start (sau indicele nodului de start in T – daca se doreste un tablou de indicatori spre parinte clasic) D: 3 A 9 1 9 C 4 Calin Jebelean E 9 1 3 ∞ ∞ 9 ∞ D T: A A A A 1 A B C D E F G H 5 G 5 2 B - 1 F 2 4 1 Algoritmul lui Dijkstra H Nodurile marcate astfel sunt noduri vizitate in graf de algoritmul lui Dijkstra 10

Algoritmul lui Dijkstra Cu alte cuvinte, presupunem ca drumurile minime de la nodul A la celelalte noduri din graf sunt alcatuite dintr-un singur arc, adica arcul direct de la A la fiecare din nodurile respective (simbolul ∞ semnifica lipsa arcului) Astfel, drumurile minime gasite dupa primul pas sunt cele ingrosate pe figura anterioara Calin Jebelean Algoritmul lui Dijkstra 11

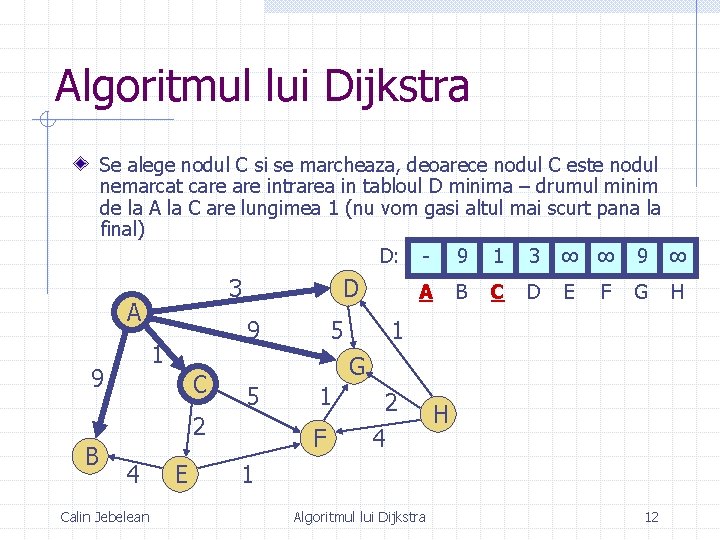
Algoritmul lui Dijkstra Se alege nodul C si se marcheaza, deoarece nodul C este nodul nemarcat care intrarea in tabloul D minima – drumul minim de la A la C are lungimea 1 (nu vom gasi altul mai scurt pana la final) D: - 9 1 3 ∞ ∞ 9 ∞ 3 A 9 1 9 D C 4 Calin Jebelean E B C D E F G 1 G 5 2 B 5 A 1 F 2 4 H 1 Algoritmul lui Dijkstra 12 H

Algoritmul lui Dijkstra Tabloul D este: - 9 1 3 ∞ ∞ 9 ∞ A B C D E G H F Pentru toate nodurile nemarcate trebuie sa verificam daca nu exista un drum mai scurt care trece prin nodul C Exemplu pentru nodul B: n n n D[B] = 9 este drumul cel mai scurt de la A la B pe care-l aveam D[C] + Arc(C , B) = 1 + ∞ = ∞ este drumul alternativ care trece prin nodul C (nodul ales) Acest al doilea drum este mai lung decat drumul pe care-l aveam deci D[B] nu se modifica la acest pas Calin Jebelean Algoritmul lui Dijkstra 13

Algoritmul lui Dijkstra Exemplu pentru nodul E: n n n D[E] = ∞ este drumul cel mai scurt de la A la E pe care-l aveam D[C] + Arc(C , E) = 1 + 2 = 3 este drumul alternativ care trece prin nodul C (nodul ales) Deoarece noul drum este mai scurt decat drumul pe care-l aveam rezulta ca D[E] se modifica din ∞ in 3 si T[E] se modifica in C (nodul ales) Se observa ca drumul alternativ trece prin nodul C (nodul ales) Drumul de la A la C de lungime D[C] fiind minim, daca adaugam arcul C->E obtinem obligatoriu drumul minim de la A la E care trece prin C Calin Jebelean Algoritmul lui Dijkstra 14

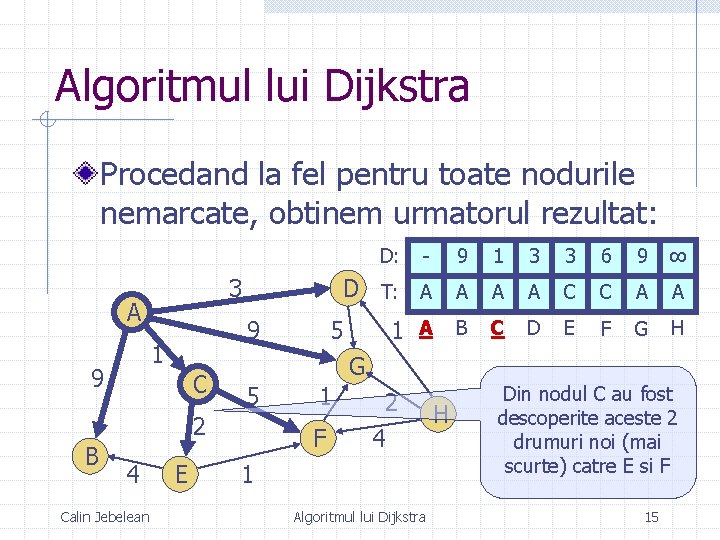
Algoritmul lui Dijkstra Procedand la fel pentru toate nodurile nemarcate, obtinem urmatorul rezultat: D: 3 A 9 1 9 C 4 Calin Jebelean E 9 1 3 3 6 9 ∞ D T: A A C C A A 1 A B C D E F G H 5 G 5 2 B - 1 F 2 4 1 Algoritmul lui Dijkstra H Din nodul C au fost descoperite aceste 2 drumuri noi (mai scurte) catre E si F 15

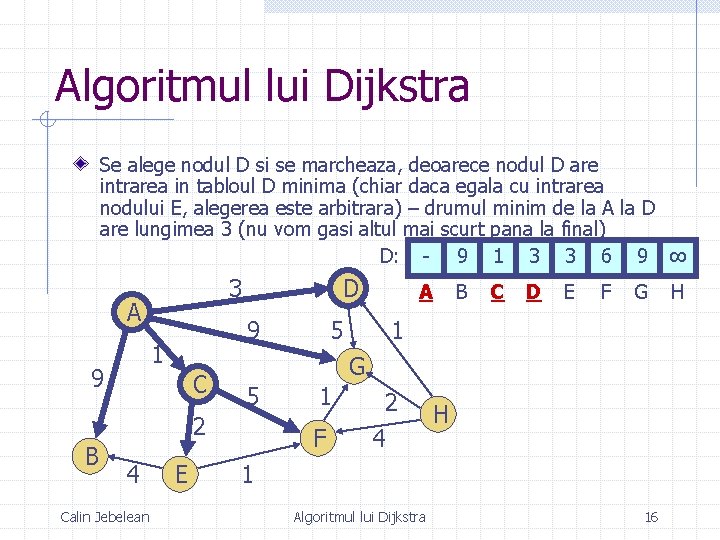
Algoritmul lui Dijkstra Se alege nodul D si se marcheaza, deoarece nodul D are intrarea in tabloul D minima (chiar daca egala cu intrarea nodului E, alegerea este arbitrara) – drumul minim de la A la D are lungimea 3 (nu vom gasi altul mai scurt pana la final) D: - 9 1 3 3 6 9 ∞ 3 A 9 1 9 D C 4 Calin Jebelean E B C D E F G 1 G 5 2 B 5 A 1 F 2 4 H 1 Algoritmul lui Dijkstra 16 H

Algoritmul lui Dijkstra Tabloul D este: - 9 1 3 3 6 9 ∞ A B C D E F G H Pentru toate nodurile nemarcate trebuie sa verificam daca nu exista un drum mai scurt care trece prin nodul D Exemplu pentru nodul F: n n n D[F] = 6 este drumul cel mai scurt de la A la F pe care-l aveam D[D] + Arc(D , F) = 3 + ∞ = ∞ este drumul alternativ care trece prin nodul D (nodul ales) Acest al doilea drum este mai lung decat drumul pe care-l aveam deci D[F] nu se modifica la acest pas Calin Jebelean Algoritmul lui Dijkstra 17

Algoritmul lui Dijkstra Exemplu pentru nodul G: n n n D[G] = 9 este drumul cel mai scurt de la A la G pe care-l aveam D[D] + Arc(D , G) = 3 + 5 = 8 este drumul alternativ care trece prin nodul D (nodul ales) Deoarece noul drum este mai scurt decat drumul pe care-l aveam rezulta ca D[G] se modifica din 9 in 8 si T[G] se modifica in D (nodul ales) Se observa ca drumul alternativ trece prin nodul D (nodul ales) Drumul de la A la D de lungime D[D] fiind minim, daca adaugam arcul D->G obtinem obligatoriu drumul minim de la A la G care trece prin D Calin Jebelean Algoritmul lui Dijkstra 18

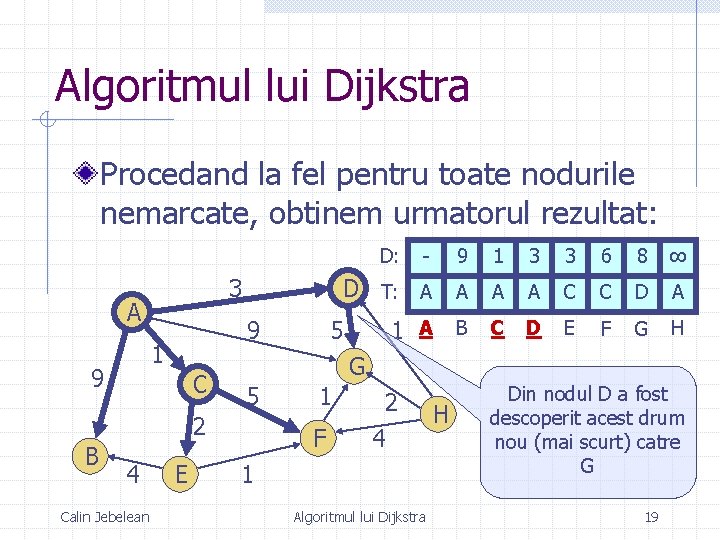
Algoritmul lui Dijkstra Procedand la fel pentru toate nodurile nemarcate, obtinem urmatorul rezultat: D: 3 A 9 1 9 C 4 Calin Jebelean E 9 1 3 3 6 8 ∞ D T: A A C C D A 1 A B C D E F G H 5 G 5 2 B - 1 F 2 4 1 Algoritmul lui Dijkstra H Din nodul D a fost descoperit acest drum nou (mai scurt) catre G 19

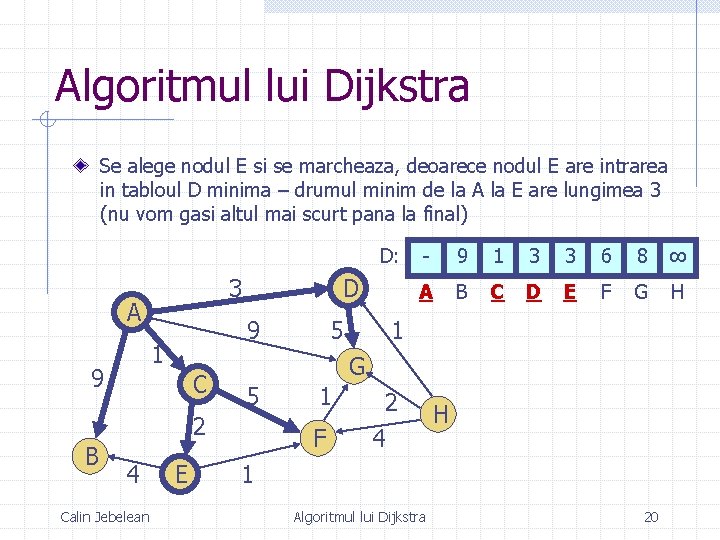
Algoritmul lui Dijkstra Se alege nodul E si se marcheaza, deoarece nodul E are intrarea in tabloul D minima – drumul minim de la A la E are lungimea 3 (nu vom gasi altul mai scurt pana la final) D: 3 A 9 1 9 D C 4 Calin Jebelean E 9 1 3 3 6 8 ∞ A B C D E F G H 1 G 5 2 B 5 - 1 F 2 4 H 1 Algoritmul lui Dijkstra 20

Algoritmul lui Dijkstra Tabloul D este: - 9 1 3 3 6 8 ∞ A B C D E F G H Pentru toate nodurile nemarcate trebuie sa verificam daca nu exista un drum mai scurt care trece prin nodul E Exemplu pentru nodul G: n n n D[G] = 8 este drumul cel mai scurt de la A la G pe care-l aveam D[E] + Arc(E , G) = 3 + ∞ = ∞ este drumul alternativ care trece prin nodul E (nodul ales) Acest al doilea drum este mai lung decat drumul pe care-l aveam deci D[G] nu se modifica la acest pas Calin Jebelean Algoritmul lui Dijkstra 21

Algoritmul lui Dijkstra Exemplu pentru nodul B: n n n D[B] = 9 este drumul cel mai scurt de la A la B pe care-l aveam D[E] + Arc(E , B) = 3 + 4 = 7 este drumul alternativ care trece prin nodul E (nodul ales) Deoarece noul drum este mai scurt decat drumul pe care-l aveam rezulta ca D[B] se modifica din 9 in 7 si T[B] se modifica in E (nodul ales) Se observa ca drumul alternativ trece prin nodul E (nodul ales) Drumul de la A la E de lungime D[E] fiind minim, daca adaugam arcul E->B obtinem obligatoriu drumul minim de la A la B care trece prin E Calin Jebelean Algoritmul lui Dijkstra 22

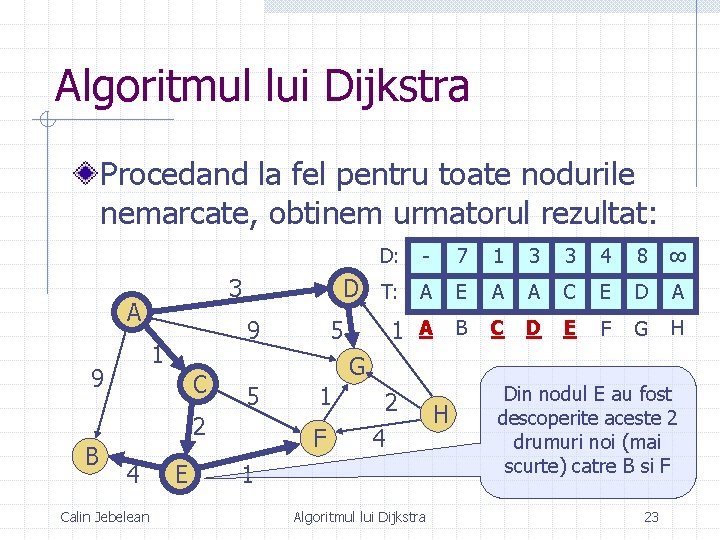
Algoritmul lui Dijkstra Procedand la fel pentru toate nodurile nemarcate, obtinem urmatorul rezultat: D: 3 A 9 1 9 C 4 Calin Jebelean E 7 1 3 3 4 8 ∞ D T: A E A A C E D A 1 A B C D E F G H 5 G 5 2 B - 1 F 2 4 1 Algoritmul lui Dijkstra H Din nodul E au fost descoperite aceste 2 drumuri noi (mai scurte) catre B si F 23

Algoritmul lui Dijkstra Se alege nodul F si se marcheaza, deoarece nodul F are intrarea in tabloul D minima – drumul minim de la A la F are lungimea 4 (nu vom gasi altul mai scurt pana la final) D: 3 A 9 1 9 D C 4 Calin Jebelean E 7 1 3 3 4 8 ∞ A B C D E F G H 1 G 5 2 B 5 - 1 F 2 4 H 1 Algoritmul lui Dijkstra 24

Algoritmul lui Dijkstra Tabloul D este: - 7 1 3 3 4 8 ∞ A B C D E F G H Pentru toate nodurile nemarcate trebuie sa verificam daca nu exista un drum mai scurt care trece prin nodul F Exemplu pentru nodul B: n n n D[B] = 7 este drumul cel mai scurt de la A la B pe care-l aveam D[F] + Arc(F , B) = 4 + ∞ = ∞ este drumul alternativ care trece prin nodul F (nodul ales) Acest al doilea drum este mai lung decat drumul pe care-l aveam deci D[B] nu se modifica la acest pas Calin Jebelean Algoritmul lui Dijkstra 25

Algoritmul lui Dijkstra Exemplu pentru nodul G: n n n D[G] = 8 este drumul cel mai scurt de la A la G pe care-l aveam D[F] + Arc(F , G) = 4 + 1 = 5 este drumul alternativ care trece prin nodul F (nodul ales) Deoarece noul drum este mai scurt decat drumul pe care-l aveam rezulta ca D[G] se modifica din 8 in 5 si T[G] se modifica in F (nodul ales) Se observa ca drumul alternativ trece prin nodul F (nodul ales) Drumul de la A la F de lungime D[F] fiind minim, daca adaugam arcul F->G obtinem obligatoriu drumul minim de la A la G care trece prin F Calin Jebelean Algoritmul lui Dijkstra 26

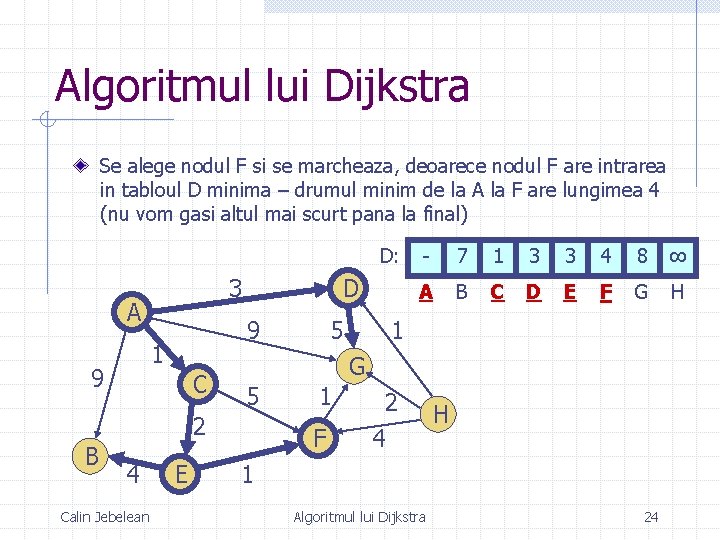
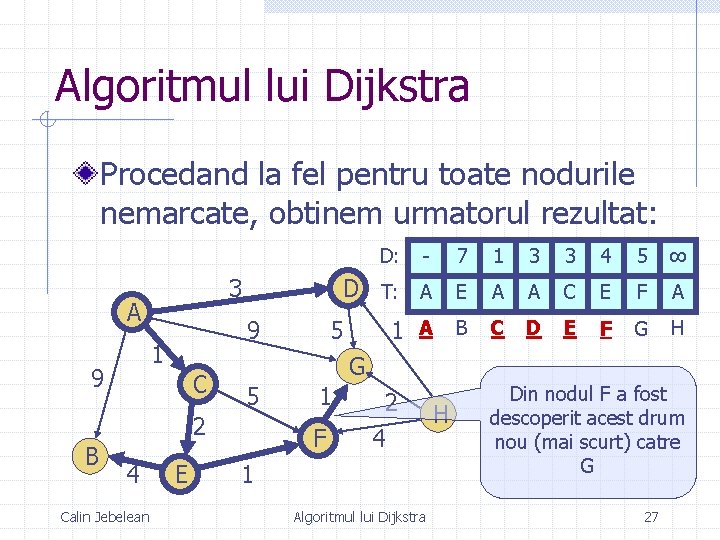
Algoritmul lui Dijkstra Procedand la fel pentru toate nodurile nemarcate, obtinem urmatorul rezultat: D: 3 A 9 1 9 C 4 Calin Jebelean E 7 1 3 3 4 5 ∞ D T: A E A A C E F A 1 A B C D E F G H 5 G 5 2 B - 1 F 2 4 1 Algoritmul lui Dijkstra H Din nodul F a fost descoperit acest drum nou (mai scurt) catre G 27

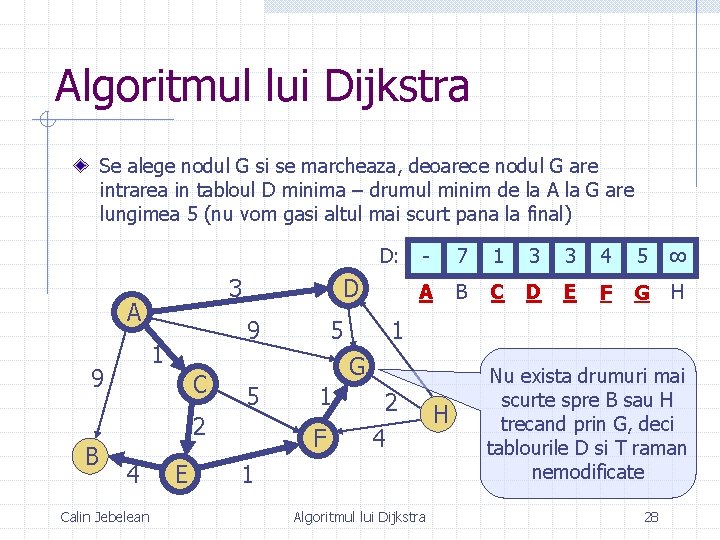
Algoritmul lui Dijkstra Se alege nodul G si se marcheaza, deoarece nodul G are intrarea in tabloul D minima – drumul minim de la A la G are lungimea 5 (nu vom gasi altul mai scurt pana la final) D: 3 A 9 1 9 D C 4 Calin Jebelean E 7 1 3 3 4 5 ∞ A B C D E F G H 1 G 5 2 B 5 - 1 F 2 4 1 Algoritmul lui Dijkstra H Nu exista drumuri mai scurte spre B sau H trecand prin G, deci tablourile D si T raman nemodificate 28

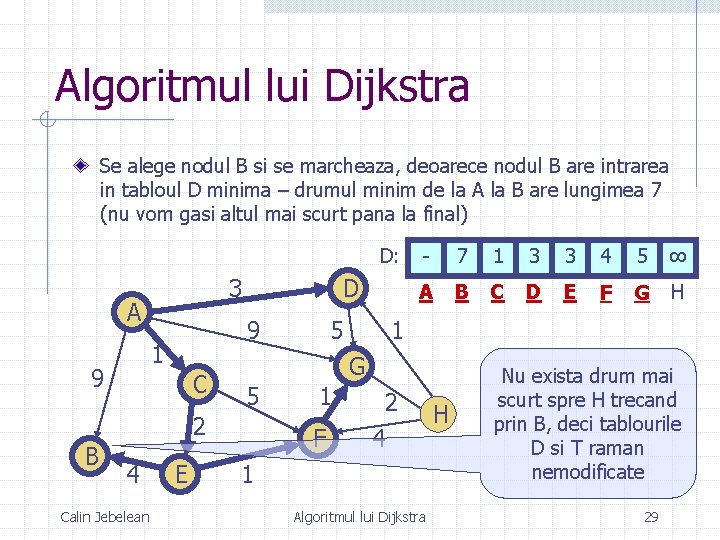
Algoritmul lui Dijkstra Se alege nodul B si se marcheaza, deoarece nodul B are intrarea in tabloul D minima – drumul minim de la A la B are lungimea 7 (nu vom gasi altul mai scurt pana la final) D: 3 A 9 1 9 D C 4 Calin Jebelean E 7 1 3 3 4 5 ∞ A B C D E F G H 1 G 5 2 B 5 - 1 F 2 4 1 Algoritmul lui Dijkstra H Nu exista drum mai scurt spre H trecand prin B, deci tablourile D si T raman nemodificate 29

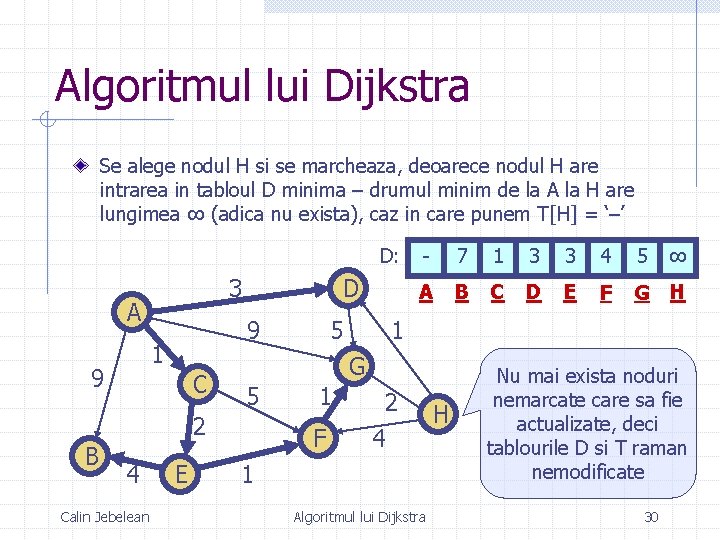
Algoritmul lui Dijkstra Se alege nodul H si se marcheaza, deoarece nodul H are intrarea in tabloul D minima – drumul minim de la A la H are lungimea ∞ (adica nu exista), caz in care punem T[H] = ‘–’ D: 3 A 9 1 9 D C 4 Calin Jebelean E 7 1 3 3 4 5 ∞ A B C D E F G H 1 G 5 2 B 5 - 1 F 2 4 1 Algoritmul lui Dijkstra H Nu mai exista noduri nemarcate care sa fie actualizate, deci tablourile D si T raman nemodificate 30

Algoritmul lui Dijkstra Algoritmul se incheie deoarece nu mai sunt noduri nemarcate Rezultatul este: D: - 7 1 3 3 4 5 ∞ T: A E A A C E F - A B C D E F G H Lungimile drumurilor minime de la A la celelalte noduri din graf sunt disponibile in tabloul D Tabloul T serveste la reconstituirea drumurilor Calin Jebelean Algoritmul lui Dijkstra 31

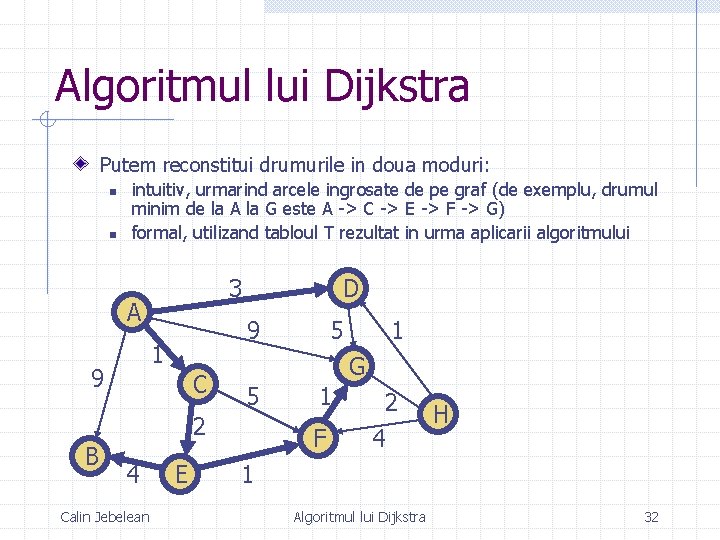
Algoritmul lui Dijkstra Putem reconstitui drumurile in doua moduri: n n intuitiv, urmarind arcele ingrosate de pe graf (de exemplu, drumul minim de la A la G este A -> C -> E -> F -> G) formal, utilizand tabloul T rezultat in urma aplicarii algoritmului 3 A 9 1 9 D C 4 Calin Jebelean E 1 G 5 2 B 5 1 F 2 4 H 1 Algoritmul lui Dijkstra 32

Algoritmul lui Dijkstra Tabloul T este: A E A A C E F - A B C D E F G H Daca consideram ca acest tablou reprezinta un arbore generalizat in implementarea cu indicatori spre parinte, atunci drumul minim de la A la G poate fi reconstituit pornind de la G: w T[G] = F w T[F] = E w T[E] = C w T[C] = A Mergand invers, obtinem: A -> C -> E -> F -> G Arborele generalizat obtinut in tabloul T contine toate drumurile minime cu originea in A Calin Jebelean Algoritmul lui Dijkstra 33

Algoritmul lui Dijkstra Algoritmul gaseste doar drumuri minime cu originea intr-un anumit nod al grafului Daca se doresc drumuri minime cu originea in alt nod, trebuie repornit algoritmul cu respectivul nod pe post de nod de start Drumurile minime obtinute pot fi reprezentate ca un arbore generalizat, deoarece ele se suprapun in mare parte Astfel, daca drumul minim de la X la Y trece prin Z, el trebuie obligatoriu sa cuprinda si drumul minim de la X la Z Calin Jebelean Algoritmul lui Dijkstra 34