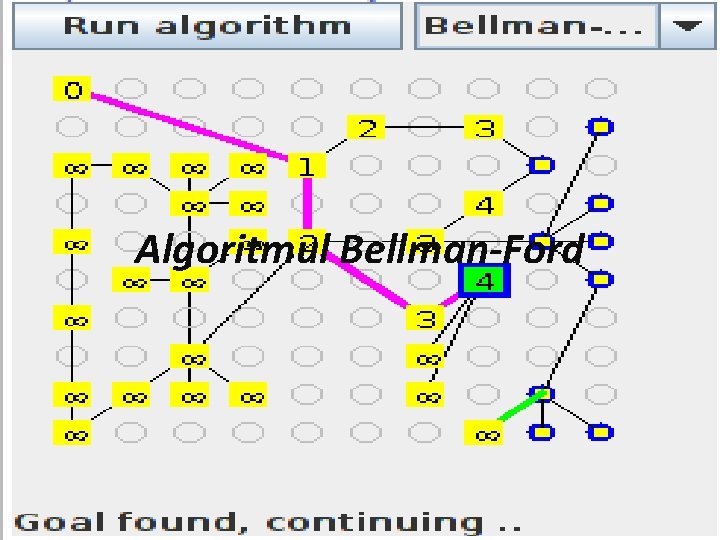
Algoritmul BellmanFord Sa intelegem Algoritmul BellmanFord determina drumurile

Algoritmul Bellman-Ford

Sa intelegem… Algoritmul Bellman-Ford determina drumurile minime de la un varf de start la toate celelalte varfuri in graf, chiar daca exista costuri negative pe arce. Exista solutie doar daca in varful de start nu se ajunge la un drum de cost negativ, deoarece acesta ar duce la minimizarea drumului la infinit.

…mai mult… Algoritmul incearca sa reduca succesiv costul drumului de la nodul de plecare la orice varf k din graf (d[k]) pana la obtinerea costului minim, astfel se verifica pentru fiecare arc(j, k) daca participa la minimizarea distantei de la nodul de plecare la nodul k (adica daca respecta conditia d[k]>d[j]+c[j][k]).

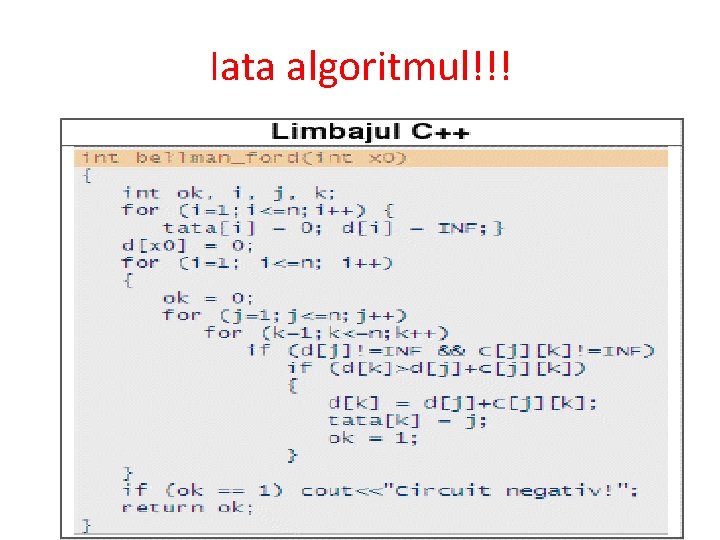
Iata algoritmul!!!

Drumul… Drumul se poate realiza atat iterativ, cat si recursiv. In ambele variante vom reconsrui drumul “inapoi”, plecand de la varful destinatiei y. in vectorul tata[y] este memorat predecesorul varfului y pe drumul de cost minim de la x 0 la y si asa mai departe. Reconstruirea drumului se termina atunci cand ajungem in varful de start.

CHESTII IMPORTANTE: 1)Observati ca drumul va fi obtinut in ordine inversa. Pentru a obtine drumul in ordinea corecta in varianta iterativa, vom memora drumul intr-un vector, pe care ulterior il vom parcurge de la sfarsit la inceput;

Chestii importante 2 • 2)In varianta recursiva, vom utiliza proprietatile stivei. 3) Algoritmul Bellman Ford astfel prezentate reține câte un singur drum de cost minim de la vârful sursă la fiecare dintre celelalte vârfuri ale grafului.

Alte chestii importante • Pentru a obtine drumurile de cost minim, se vor retine pentru fiecare varf Y din graf toate varfurile care il preceda pe y pe un drum de cost minim de la X 0 la Y.

Continuare • Acest lucru se va face astfel: • tata[i][0] este numărul vârfurilor din care se poate atinge vârful i obținând • un cost minim • tata[i][k] este cel de-al k-lea nod din care se poate atinge vârful i obținând • un cost minim, unde k este strict pozitiv.

Complexitate • Complexitatea algoritmului Bellman Ford este O(n^3), deoarece algoritmul execută de n ori secvența de minimizare distanțelor având complexitatea O(n^2). • Dacă graful este memorat în liste de adiacență, complexitatea algoritmului este O(nxm).