Algoritmo de Retropropagacin Conclusiones de Retropropagacin n 1

Algoritmo de Retropropagación

Conclusiones de Retropropagación n 1. Si la neurona j es un nodo de salida es igual al producto de la derivada y la señal de error. Ambas están asociadas a la neurona j.

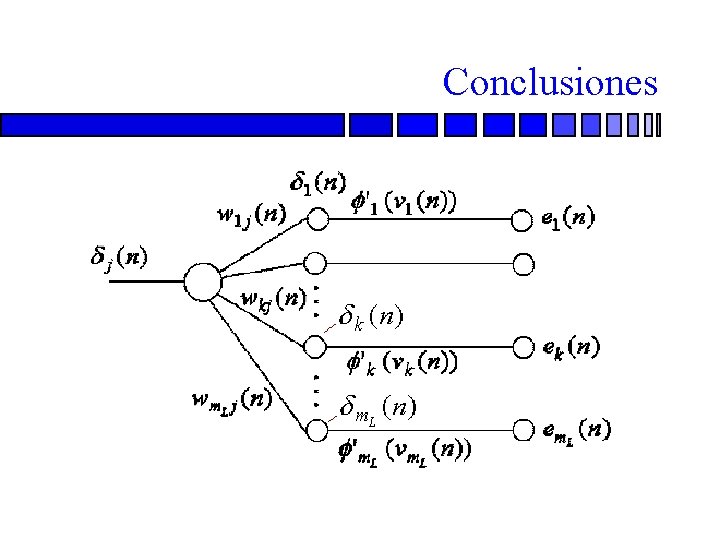
Conclusiones de Retropropagación 2. Si la neurona j es un nodo escondido, n es igual al producto de la derivada asociada n y la suma pesada de las n calculada para las neuronas de la siguiente capa escondida o de salida que se conectan a la neurona j. n

Conclusiones de Retropropagación n La corrección aplicada a definida por la regla delta: n y: está

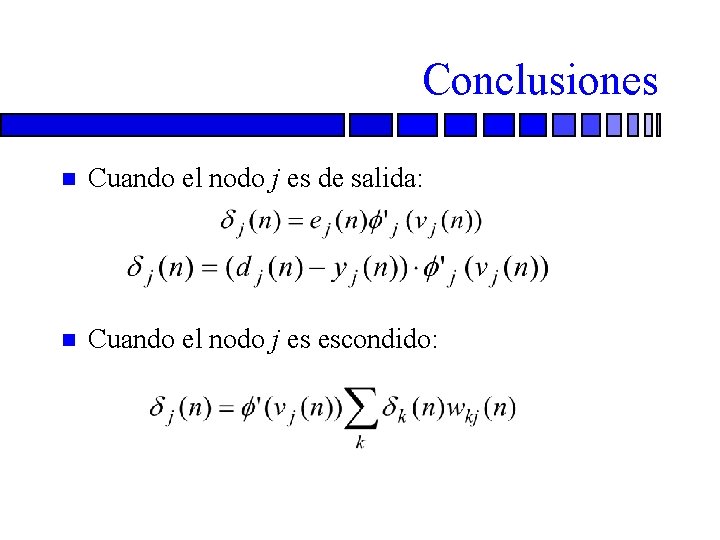
Conclusiones n Cuando el nodo j es de salida: n Cuando el nodo j es escondido:

Conclusiones

Logística n Ya que

Logística n Entonces n y n para una neurona de salida

Logística n Análogamente n y, para una neurona escondida:

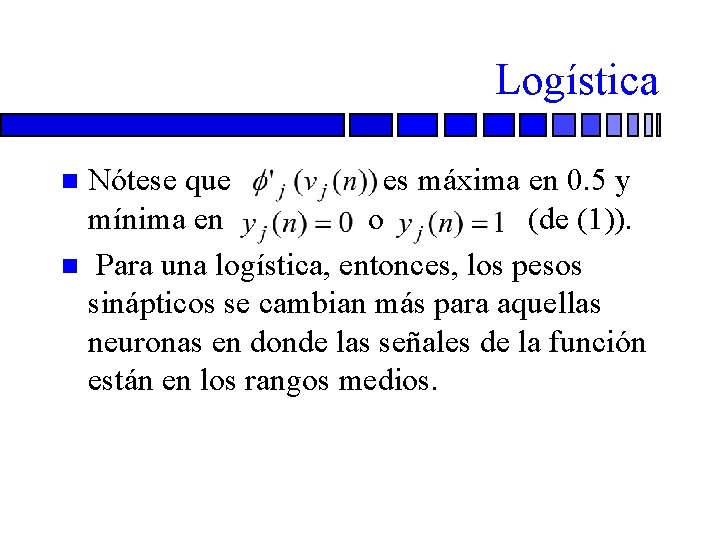
Logística Nótese que es máxima en 0. 5 y mínima en o (de (1)). n Para una logística, entonces, los pesos sinápticos se cambian más para aquellas neuronas en donde las señales de la función están en los rangos medios. n

Tangente Hiperbólica

Tangente Hiperbólica n Para la capa de salida

Tangente Hiperbólica n Para una capa escondida:

Momento El algoritmo de RP “aproxima” la trayectoria en el espacio de los pesos por el método de gradiente máximo. n A una pequeña corresponden pequeños cambios en la trayectoria del descenso y éstos son más suaves. Si es grande los cambios pueden ser inestables (oscilatorios). n

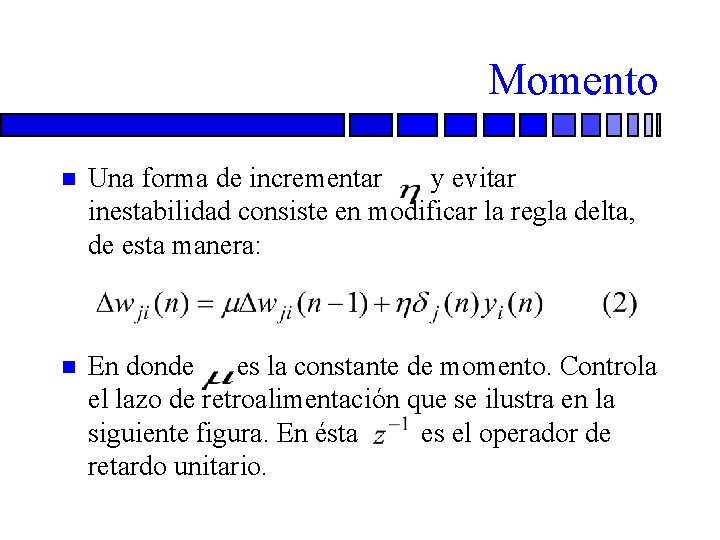
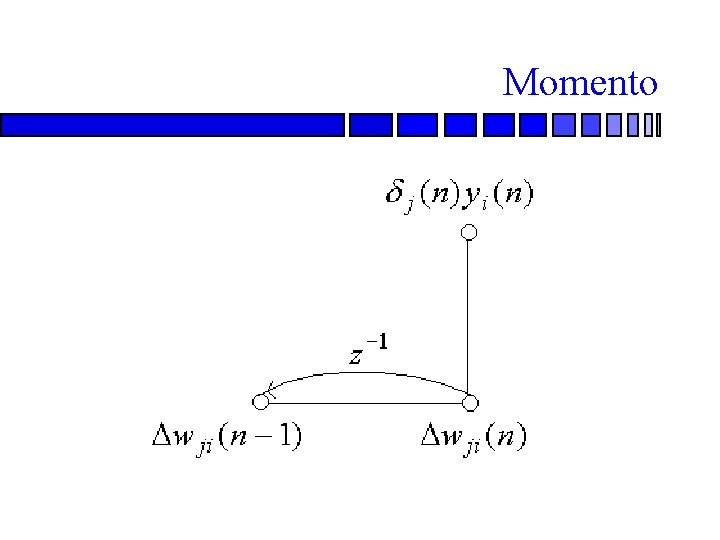
Momento n Una forma de incrementar y evitar inestabilidad consiste en modificar la regla delta, de esta manera: n En donde es la constante de momento. Controla el lazo de retroalimentación que se ilustra en la siguiente figura. En ésta es el operador de retardo unitario.

Momento

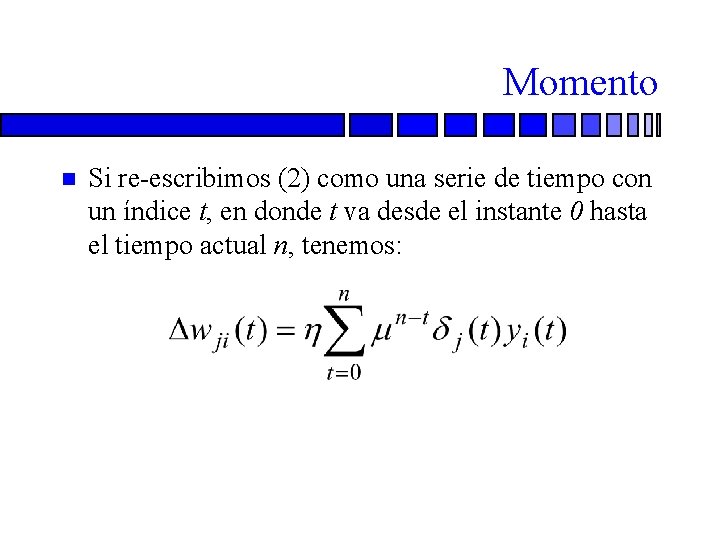
Momento n Si re-escribimos (2) como una serie de tiempo con un índice t, en donde t va desde el instante 0 hasta el tiempo actual n, tenemos:

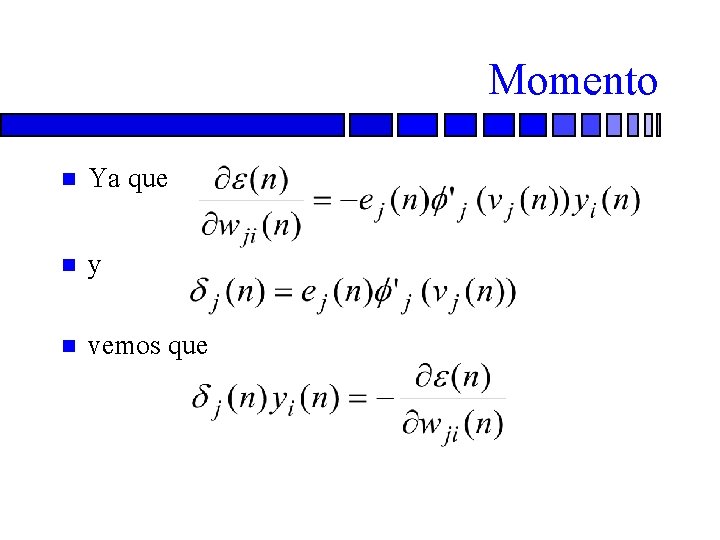
Momento n Ya que n y n vemos que

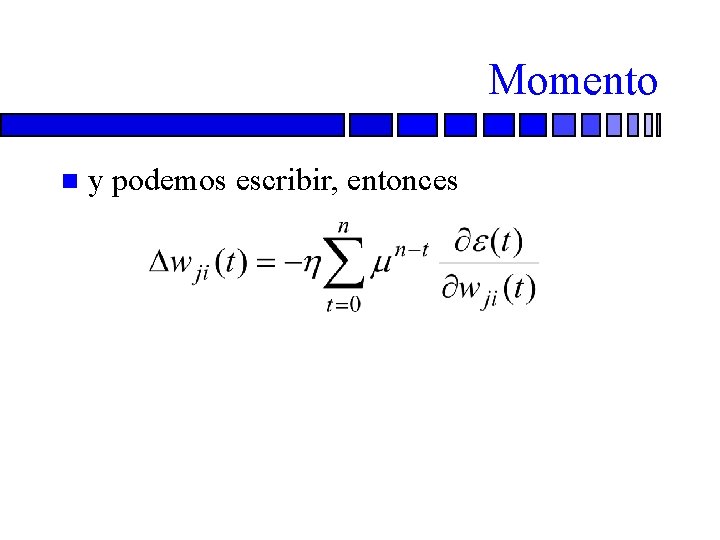
Momento n y podemos escribir, entonces

Momento n Comentarios: – El ajuste actual representa la suma de una serie de tiempo ponderada exponencialmente. Para que converja: – Cuando tiene el mismo signo en iteraciones consecutivas, crece en magnitud y se ajusta en cantidades grandes.

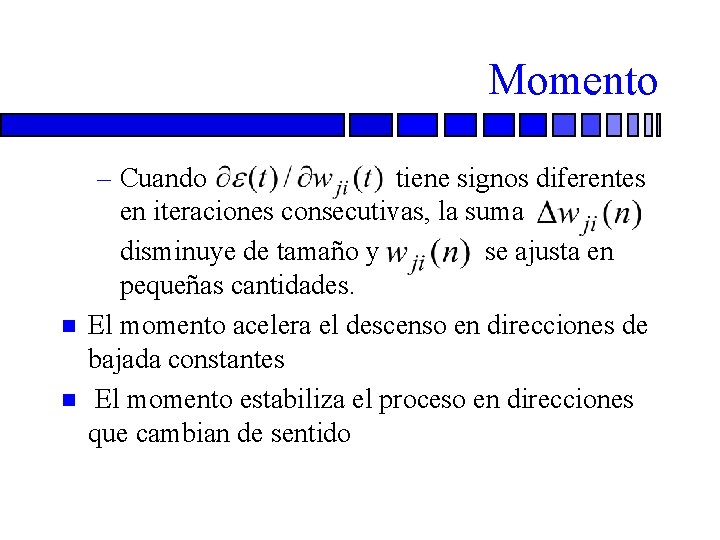
Momento n n – Cuando tiene signos diferentes en iteraciones consecutivas, la suma – disminuye de tamaño y se ajusta en pequeñas cantidades. El momento acelera el descenso en direcciones de bajada constantes El momento estabiliza el proceso en direcciones que cambian de sentido

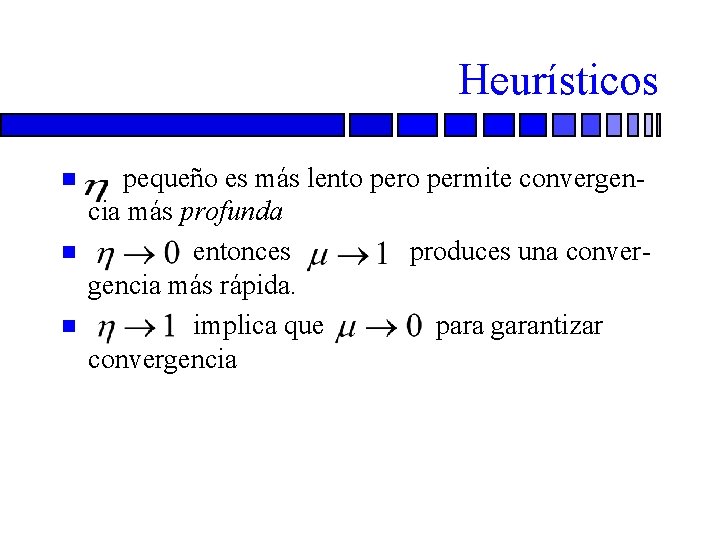
Heurísticos n n n pequeño es más lento permite convergencia más profunda entonces produces una convergencia más rápida. implica que para garantizar convergencia

Heurísticos n Tamaño del conjunto de prueba – N = tamaño de conjunto de entrenamiento – W = número de pesos en la red – – W>>1 (razón de entrenamiento)

Heurísticos Ejemplo: n W=150 n ropt=0. 07 n 93% de los datos (140) se usan para entrenamiento n 7% de los datos (10) se usan para prueba n

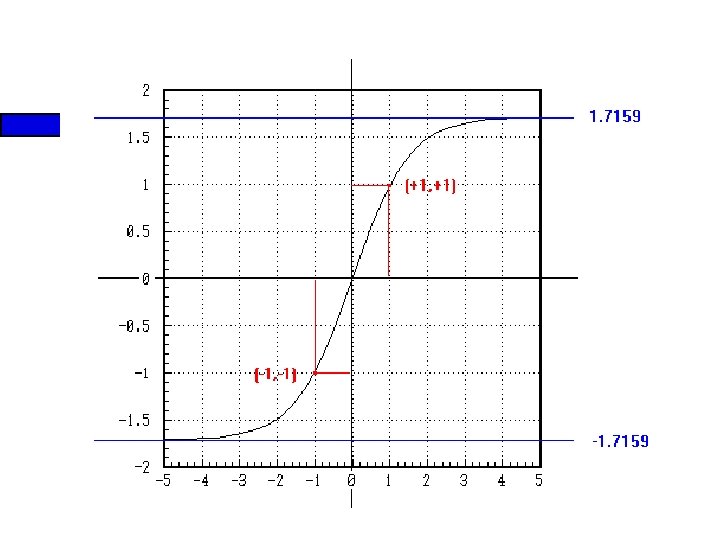
Heurísticos n Función de Activación – Una red RP puede aprender más rápidamente si la sigmoide es antisimétrica: – por ejemplo

Heurísticos n n Valores adecuados para a y b (determinados experimentalmente) son: – a=1. 7159 – b=2/3 Por lo tanto: – a) – b)

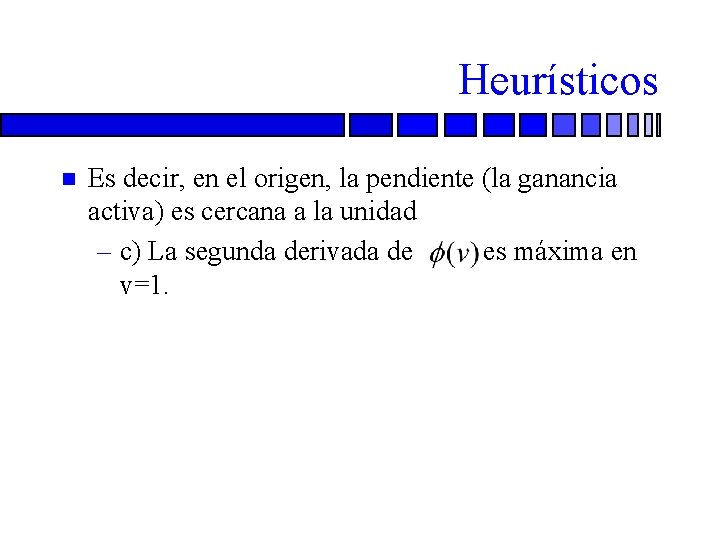
Heurísticos n Es decir, en el origen, la pendiente (la ganancia activa) es cercana a la unidad – c) La segunda derivada de es máxima en v=1.

Heurísticos

Heurísticos n n n Los valores objetivo deben ser elegidos en el rango de la función de activación La respuesta deseada en la capa L debe de ser desplazada del valor límite. Por ejemplo:

Heurísticos n n n El valor medio (sobre el conjunto de entrenamiento) debe ser 0 o pequeño comparado con Los valores no debe estar correlacionados Las variables deben escalarse de manera que sus covarianzas sean aproximadamente iguales. – Esto garantiza que las ws se aprendan a las mismas velocidades aproximadamente.

Heurísticos n Las variables deben ser equi-espaciadas en el intervalo de observación – Si esto no es posible, es conveniente usar un spline natural para completar los datos faltantes

Heurísticos (Inicialización) n Consideremos una RPR con tanh como función de activación. Si el umbral es 0 : n Sea n y

Heurísticos n Si las entradas no están correlacionadas n Tomemos las con de una distribución uniforme

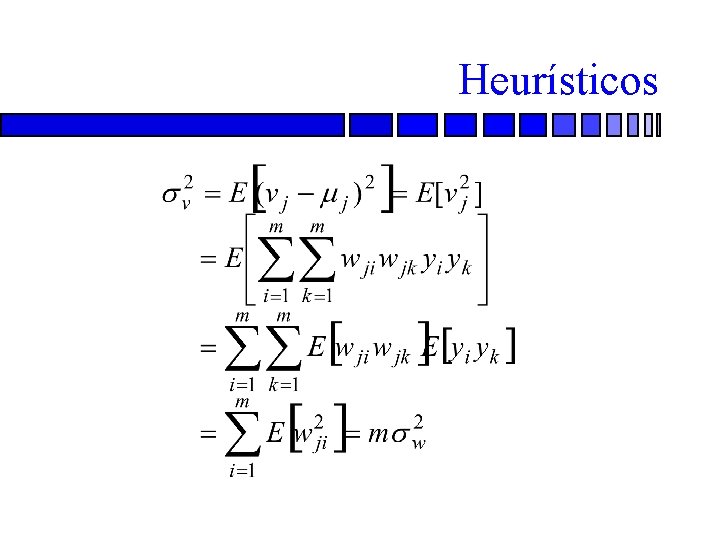
Heurísticos n Entonces la media y la varianza de n y son:

Heurísticos

Heurísticos n n en done m es el número de conexiones sinápticas a una neurona. Es decir, queremos inicializar de manera que esté en la transición de la parte lineal y saturada de su función de activación tanh. Para tanh, como se especificó antes, esto se logra (a=1. 7159; b=0. 6667) haciendo que en y

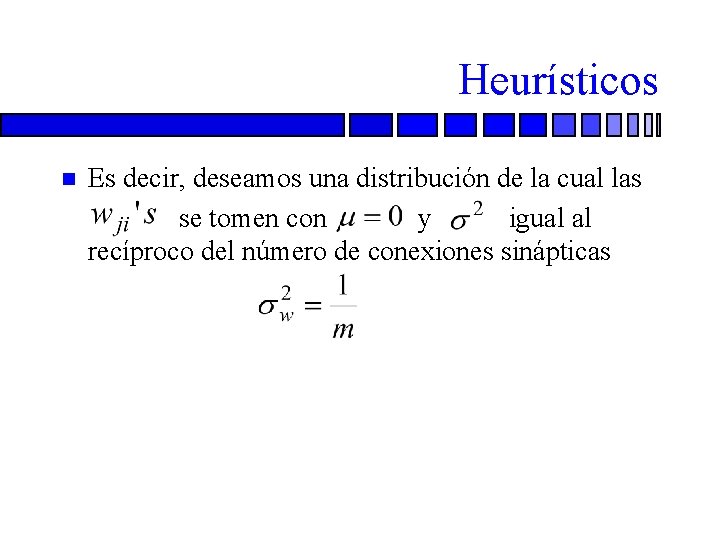
Heurísticos n n Es decir, deseamos una distribución de la cual las se tomen con y igual al recíproco del número de conexiones sinápticas

Heurísticos