Algoritmo de FloydWarshall Caminho mnimo de todos os

Algoritmo de Floyd-Warshall Caminho mínimo de todos os pares

O grupo • Bruno de Oliveira Ivamoto • Chrystian Gabriel da Silva • Bruna Borges Resende • Arthur Alves da Rogério

Introdução • Conhecido como: Floyd’s Algorithm, Roy-Warshall Algorithm, Roy-Floyd Algorithm, WFI Algorithm. • Publicado por Robert Floyd em 1962.

O Algoritmo

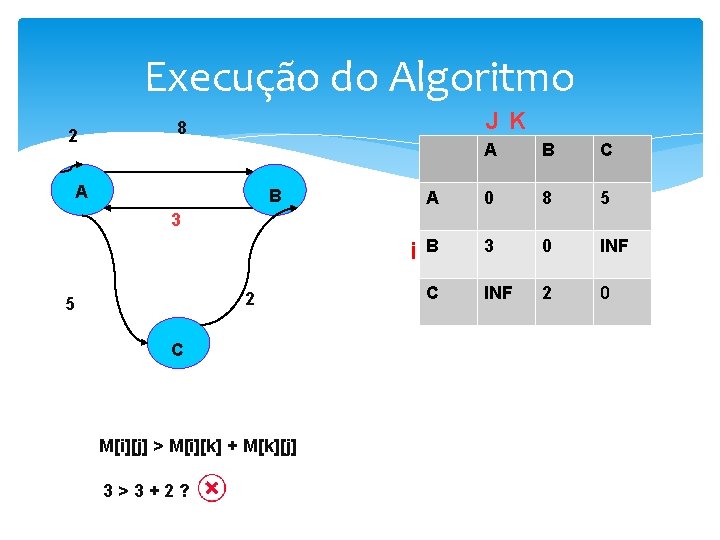
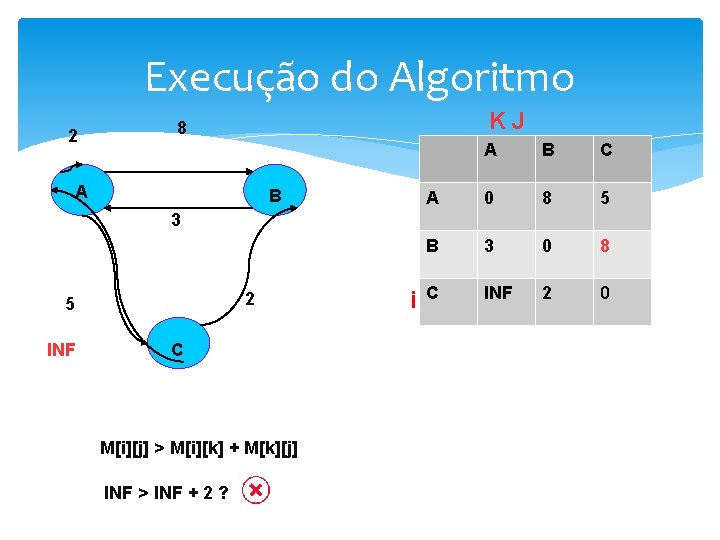
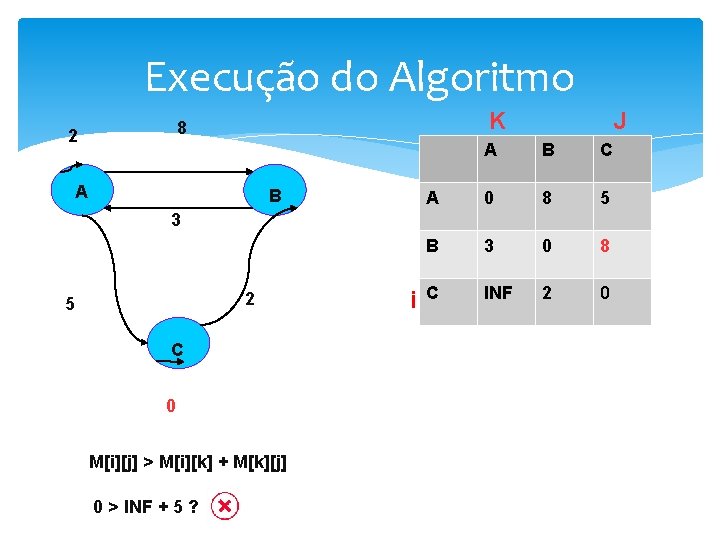
Execução do Algoritmo 2 JK 8 A B 3 2 5 C M[i][j] > M[i][k] + M[k][j] i A B C A 0 8 5 B 3 0 INF C INF 2 0

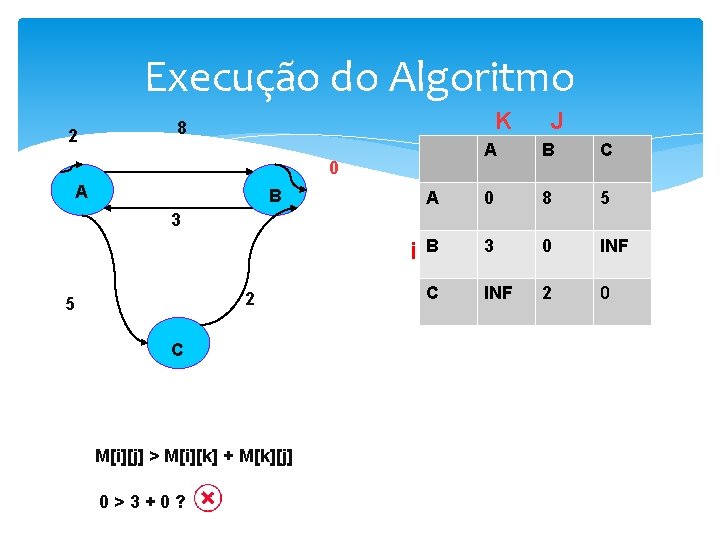
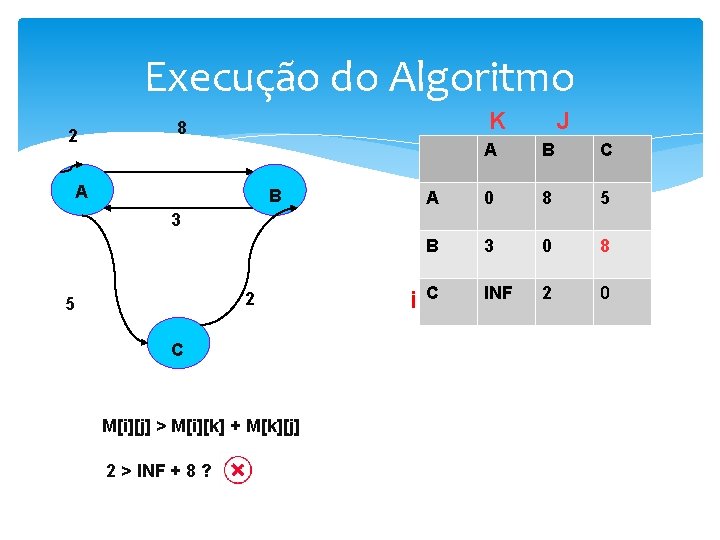
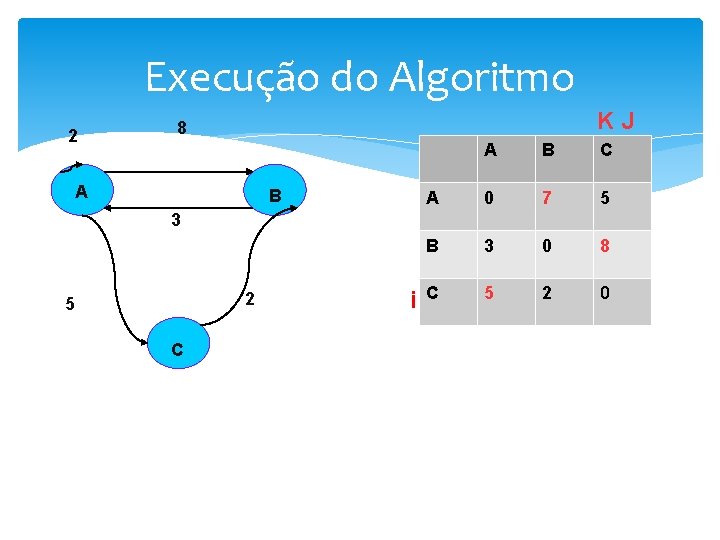
Execução do Algoritmo JK 8 2 A B 3 2 5 C M[i][j] > M[i][k] + M[k][j] 2>2+2? i A B C A 0 8 5 B 3 0 INF C INF 2 0

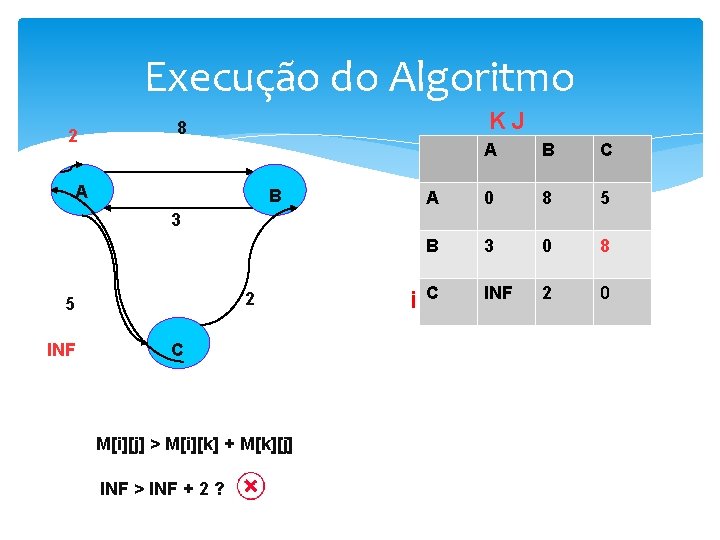
Execução do Algoritmo 2 K 8 A B 3 2 5 C M[i][j] > M[i][k] + M[k][j] 8>2+8? i J A B C A 0 8 5 B 3 0 INF C INF 2 0

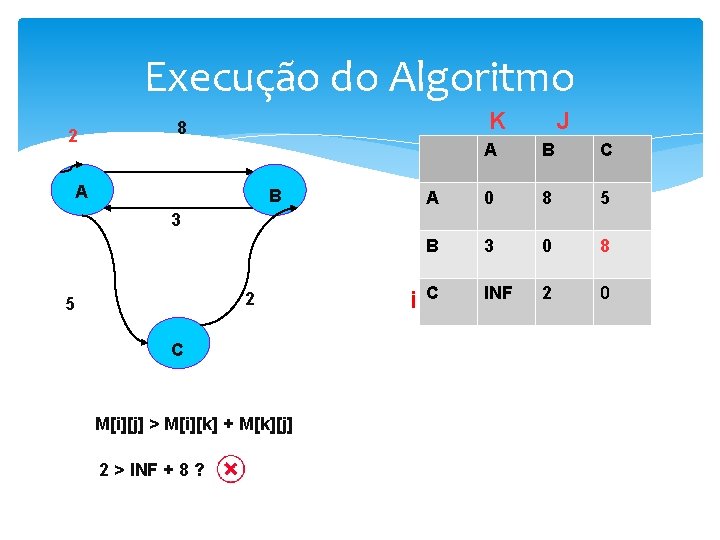
Execução do Algoritmo 2 K 8 A B 3 2 5 C M[i][j] > M[i][k] + M[k][j] 5>2+5? i J A B C A 0 8 5 B 3 0 INF C INF 2 0

Execução do Algoritmo 2 JK 8 A B C A 0 8 5 B 3 0 INF C INF 2 0 3 i 2 5 C M[i][j] > M[i][k] + M[k][j] 3>3+2?

Execução do Algoritmo 2 K 8 A B C A 0 8 5 B 3 0 INF C INF 2 0 0 A B J 3 i 2 5 C M[i][j] > M[i][k] + M[k][j] 0>3+0?

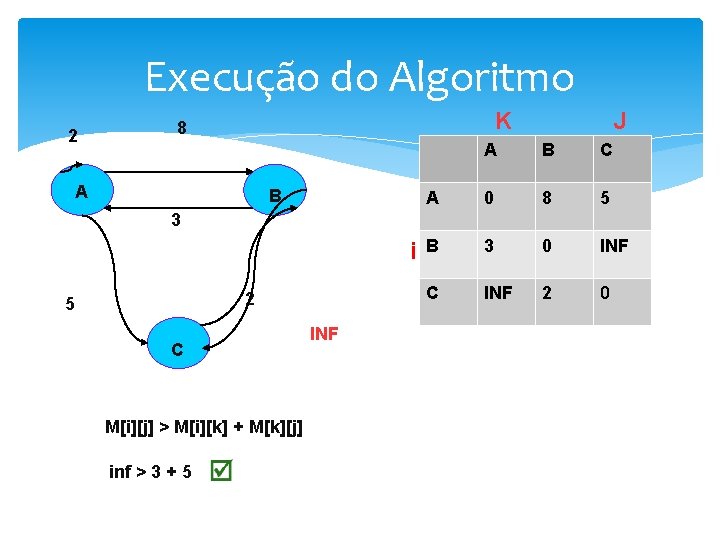
Execução do Algoritmo 2 K 8 A B J A B C A 0 8 5 B 3 0 INF C INF 2 0 3 i 2 5 C M[i][j] > M[i][k] + M[k][j] inf > 3 + 5 INF

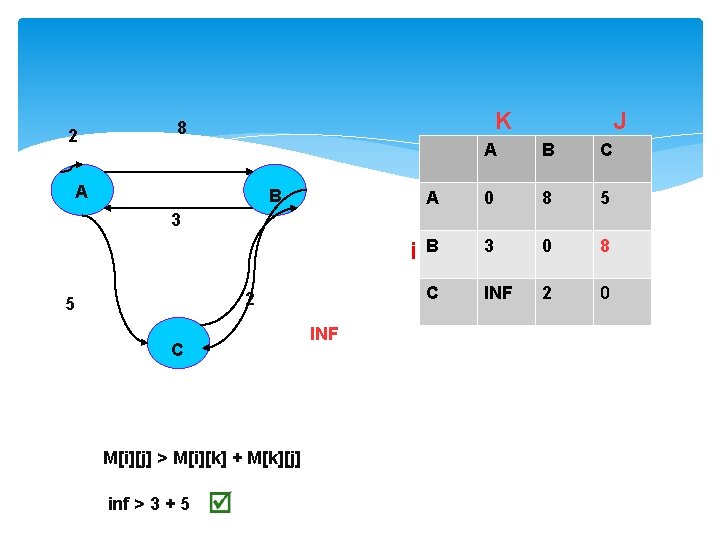
2 K 8 A B J A B C A 0 8 5 B 3 0 8 C INF 2 0 3 i 2 5 C M[i][j] > M[i][k] + M[k][j] inf > 3 + 5 INF

Execução do Algoritmo 2 KJ 8 A B C A 0 8 5 B 3 0 8 C INF 2 0 3 2 5 INF C M[i][j] > M[i][k] + M[k][j] INF > INF + 2 ? i

Execução do Algoritmo 2 K 8 A B J A B C A 0 8 5 B 3 0 8 C INF 2 0 3 2 5 C M[i][j] > M[i][k] + M[k][j] 2 > INF + 8 ? i

Execução do Algoritmo 2 KJ 8 A B C A 0 8 5 B 3 0 8 C INF 2 0 3 2 5 INF C M[i][j] > M[i][k] + M[k][j] INF > INF + 2 ? i

Execução do Algoritmo 2 K 8 A B J A B C A 0 8 5 B 3 0 8 C INF 2 0 3 2 5 C M[i][j] > M[i][k] + M[k][j] 2 > INF + 8 ? i

Execução do Algoritmo K 8 2 A B J A B C A 0 8 5 B 3 0 8 C INF 2 0 3 2 5 C 0 M[i][j] > M[i][k] + M[k][j] 0 > INF + 5 ? i

Execução do Algoritmo 2 KJ 8 A B C A 0 7 5 B 3 0 8 C 5 2 0 3 2 5 C i

Em que o algoritmo é utilizado ? • Calcular o fecho transitivo de um grafo. • Achar um vértice central, isto é, aquele que minimiza a distância máxima ou média entre todos os vértices. • Calcular o diâmetro de um grafo.

Os grafos • O grafo pode conter arestas negativas. • Não pode conter ciclos negativos. • Utiliza técnica de programação dinâmica.

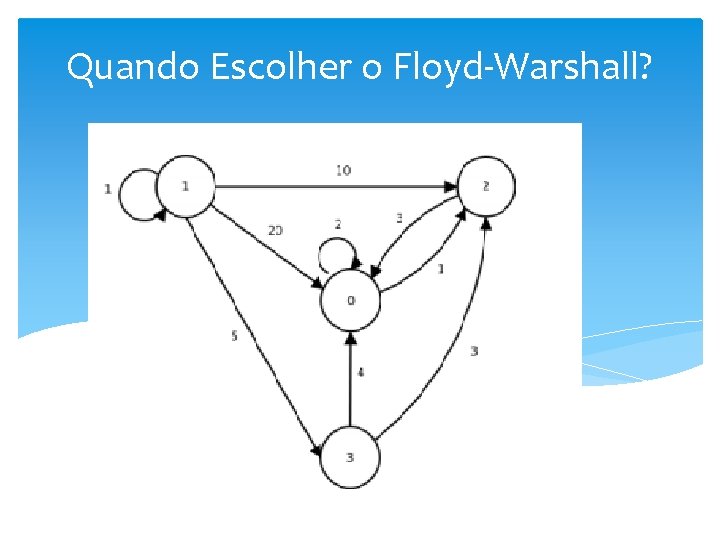
Quando Escolher o Floyd-Warshall?

Tempo de Execução • Algoritmo de Dijkstra: • Algoritmo de Floyd-Warshall: • Algoritmo de Bellman Ford: | V | O ( | V * A | )

Exemplos • Caminhos mais curtos em grafos orientados. • Proximidade transitiva de grafos orientados. • Roteamento Otimizado. • Encontrar vértice central. • Definir se um grafo não direcionado é bipartido.

Considerações Finais • Floyd-Warshall e Bellman Ford trabalha com arestas de peso negativo enquanto Dijkstra não. • No Dijkstra, é possível reproduzir o caminho, enquanto que o Floyd-Warshall fornece apenas o caminho mais curto, e não a sequência das arestas.

Bibliografia • https: //en. wikipedia. org/wiki/Floyd%E 2%80%93 Warshall_algorithm • https: //www. youtube. com/watch? v=4 OQe. Cu. LYj-4&feature=youtu. be • http: //pt. slideshare. net/Joao. Silva 30/algoritmo-de-floydwarshall

Perguntas ?