Algoritmo de Dijkstra Motivao Encontrar o caminho mnimo

Algoritmo de Dijkstra

Motivação • Encontrar o caminho mínimo, de única origem, entre essa origem e os demais vértices, num grafo dirigido ou não dirigido com arestas de peso não negativo.

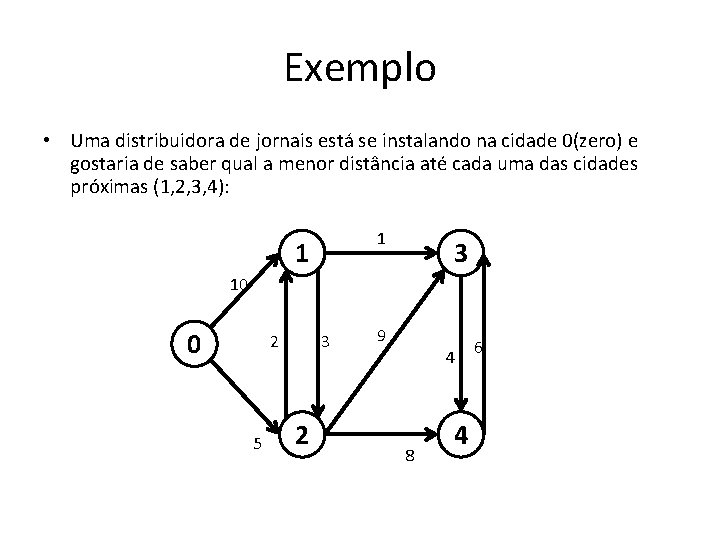
Exemplo • alguém precisa se deslocar de uma cidade para outra. Para isso, ela dispõe de várias estradas, que passam por diversas cidades. Qual delas oferece uma trajetória de menor caminho?

Restrições • Todas as arestas do grafo devem ter custos não negativos; • O algoritmo que serve para resolver o mesmo problema em um grafo com pesos negativos é o algoritmo de Bellman-Ford.

Exemplo • Uma distribuidora de jornais está se instalando na cidade 0(zero) e gostaria de saber qual a menor distância até cada uma das cidades próximas (1, 2, 3, 4): 1 1 3 10 0 2 5 3 2 9 4 8 4 6

Pseudocódigo Dijkstra Fonte: http: //en. wikipedia. org/wiki/Dijkstra%27 s_algorithm

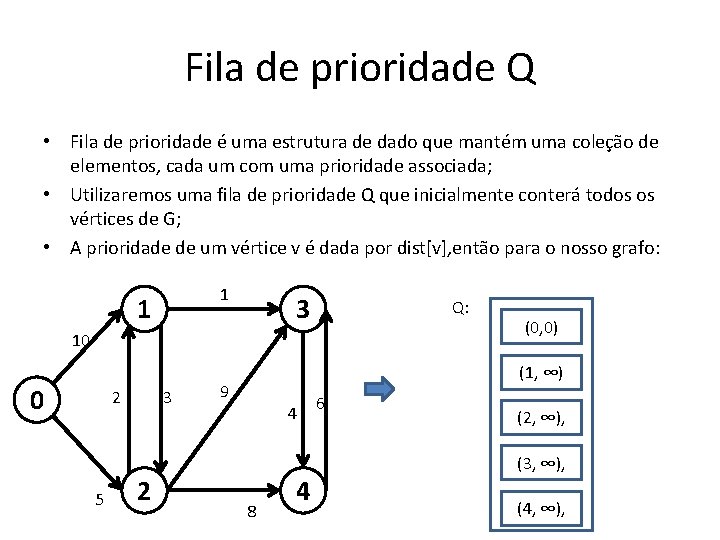
Fila de prioridade Q • Fila de prioridade é uma estrutura de dado que mantém uma coleção de elementos, cada um com uma prioridade associada; • Utilizaremos uma fila de prioridade Q que inicialmente conterá todos os vértices de G; • A prioridade de um vértice v é dada por dist[v], então para o nosso grafo: 1 1 3 Q: 10 0 2 5 3 2 (0, 0) (1, ∞) 9 4 8 4 6 (2, ∞), (3, ∞), (4, ∞),

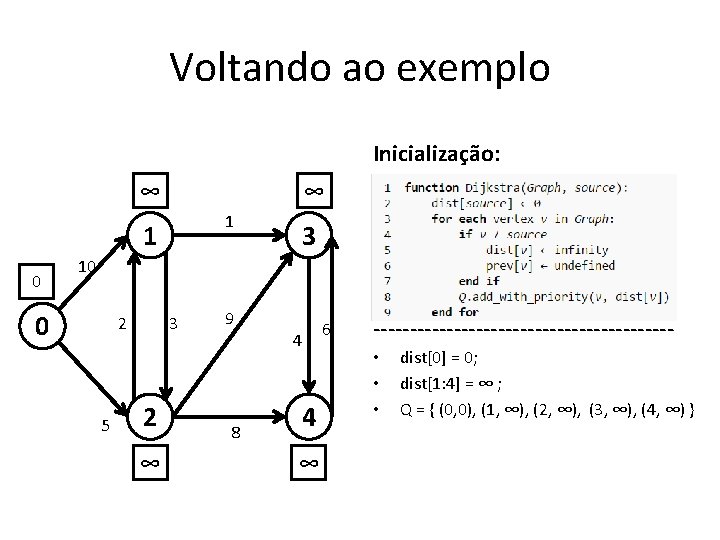
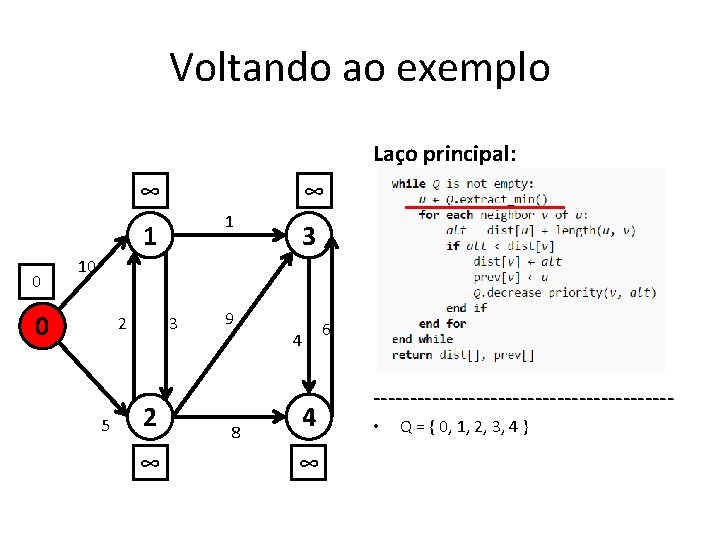
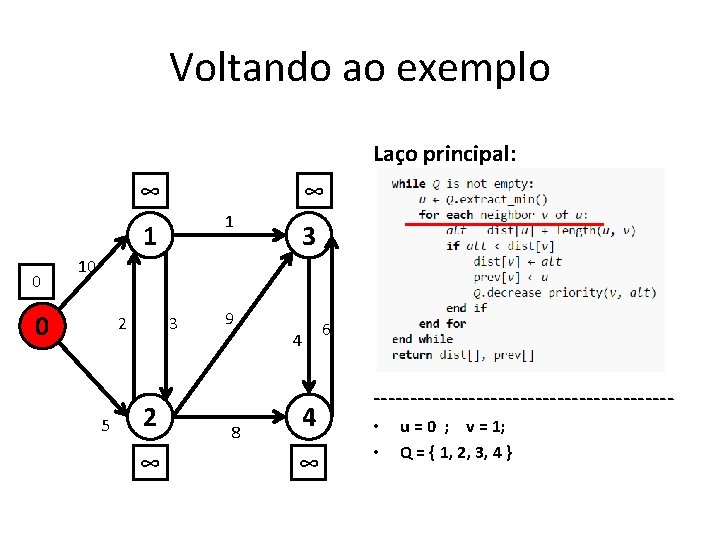
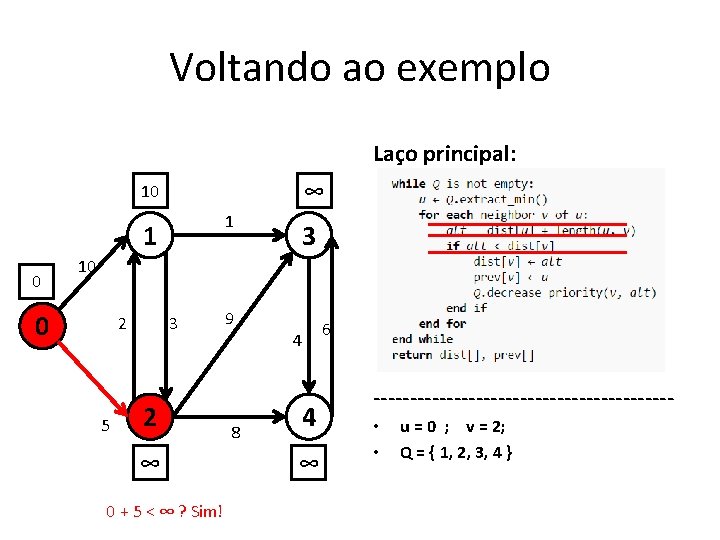
Voltando ao exemplo Laço principal: ∞ ∞ 1 1 0 3 10 0 2 5 3 2 ∞ 9 8 4 4 ∞ 6 -------------------- • Q = { 0, 1, 2, 3, 4 }

Voltando ao exemplo Laço principal: ∞ ∞ 1 1 0 3 10 0 2 5 3 2 ∞ 9 8 4 4 ∞ 6 -------------------- • • u = 0 ; v = 1; Q = { 1, 2, 3, 4 }

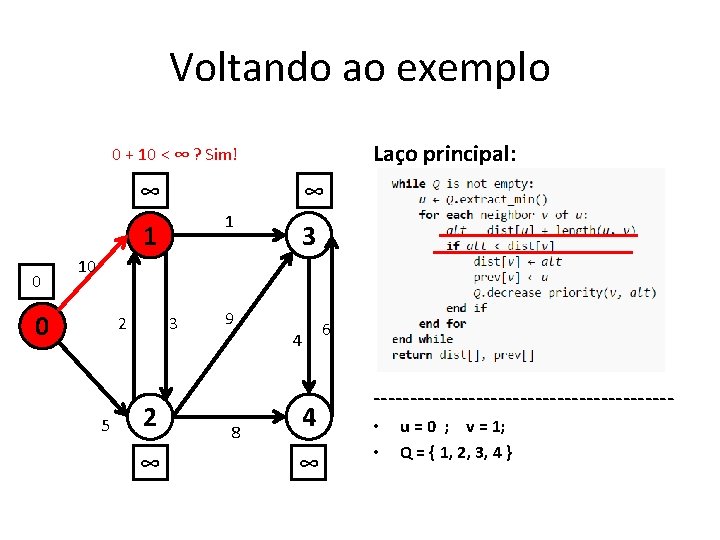
Voltando ao exemplo Laço principal: 0 + 10 < ∞ ? Sim! ∞ ∞ 1 1 0 3 10 0 2 5 3 2 ∞ 9 8 4 4 ∞ 6 -------------------- • • u = 0 ; v = 1; Q = { 1, 2, 3, 4 }

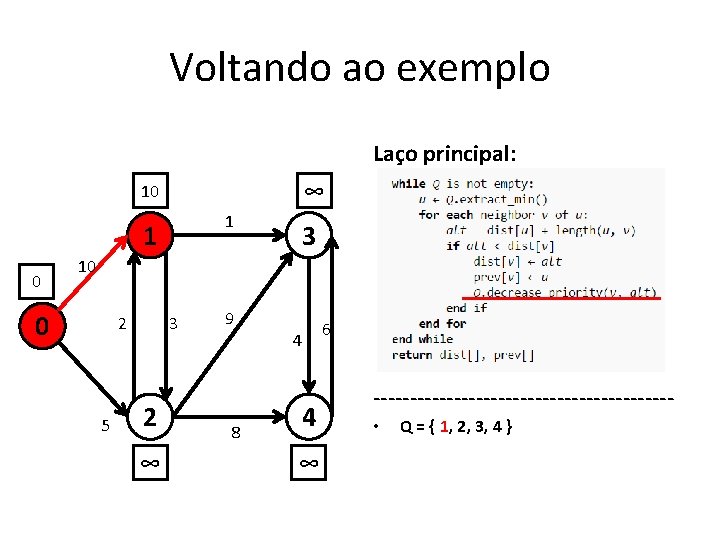
Voltando ao exemplo Laço principal: ∞ 10 1 1 0 3 10 0 2 5 3 2 ∞ 9 8 4 4 ∞ 6 -------------------- • Q = { 1, 2, 3, 4 }

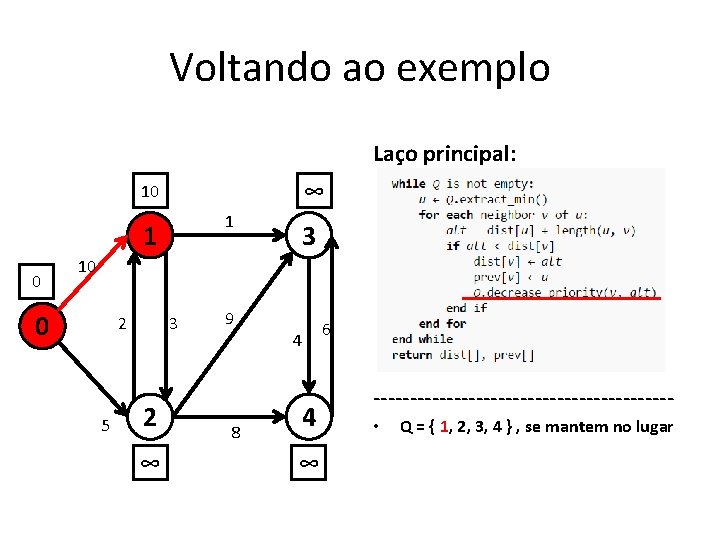
Voltando ao exemplo Laço principal: ∞ 10 1 1 0 3 10 0 2 5 3 2 ∞ 9 8 4 4 ∞ 6 -------------------- • Q = { 1, 2, 3, 4 } , se mantem no lugar

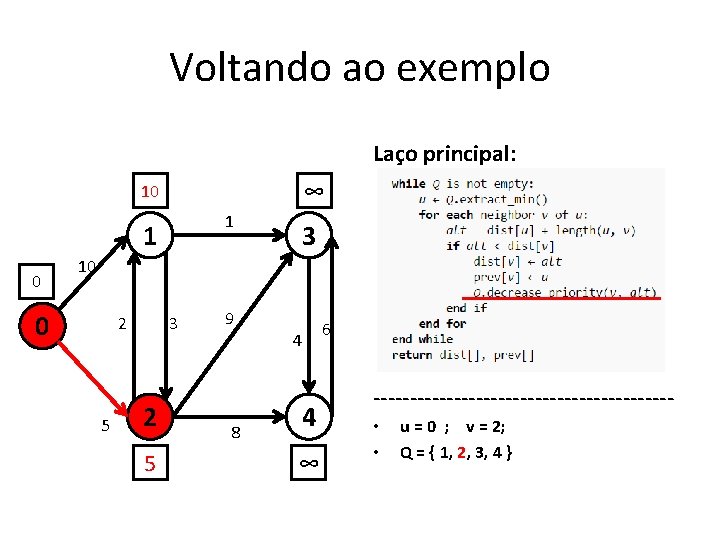
Voltando ao exemplo Laço principal: ∞ 10 1 1 0 3 10 0 2 5 3 2 ∞ 0 + 5 < ∞ ? Sim! 9 8 4 4 ∞ 6 -------------------- • • u = 0 ; v = 2; Q = { 1, 2, 3, 4 }

Voltando ao exemplo Laço principal: ∞ 10 1 1 0 3 10 0 2 5 3 2 5 9 8 4 4 ∞ 6 -------------------- • • u = 0 ; v = 2; Q = { 1, 2, 3, 4 }

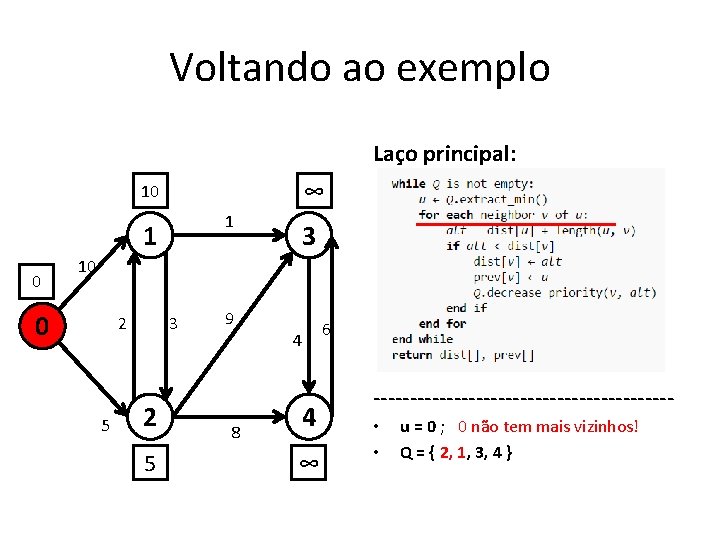
Voltando ao exemplo Laço principal: ∞ 10 1 1 0 3 10 0 2 5 3 2 5 9 8 4 4 ∞ 6 -------------------- • • u = 0 ; 0 não tem mais vizinhos! Q = { 2, 1, 3, 4 }

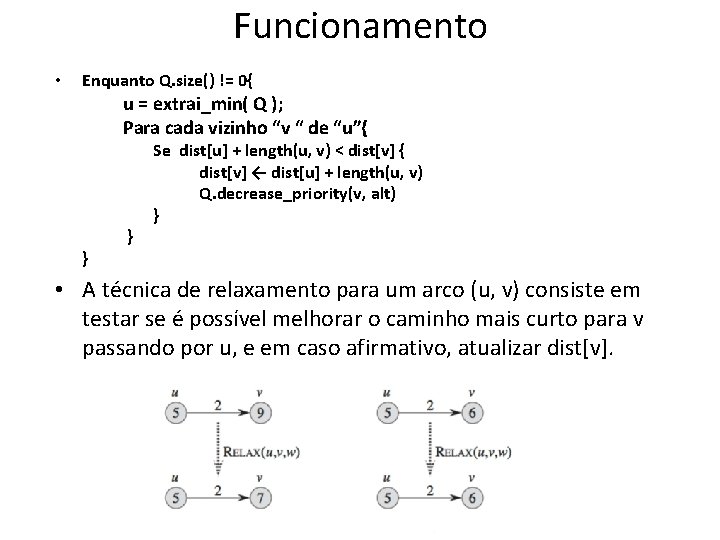
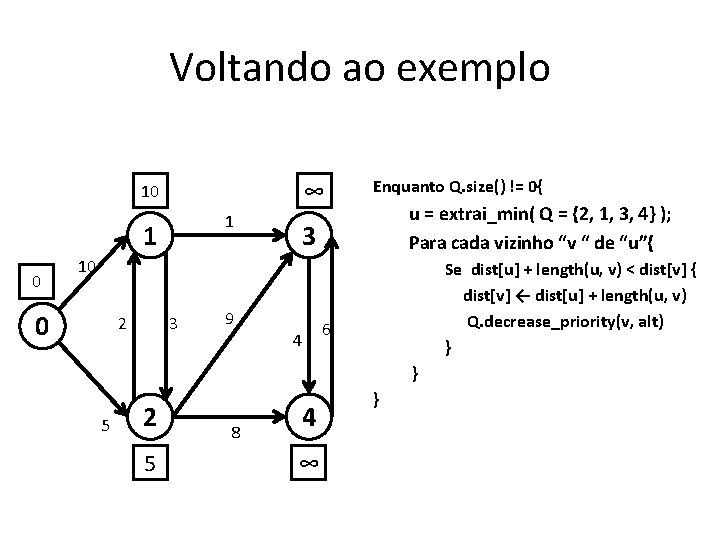
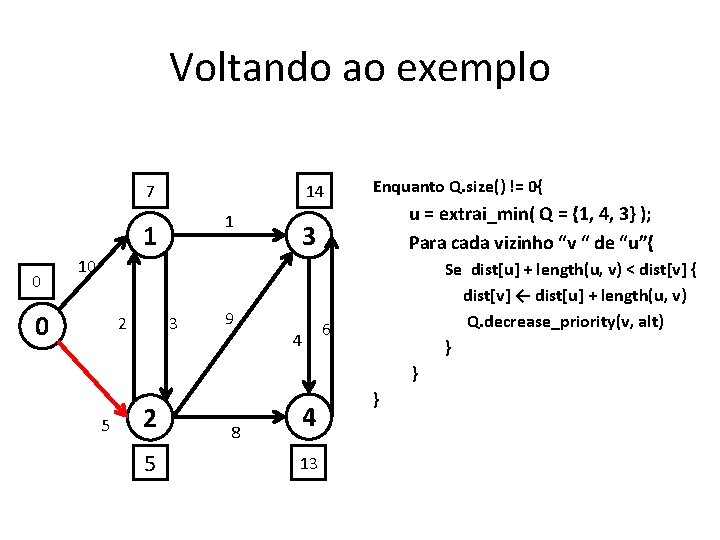
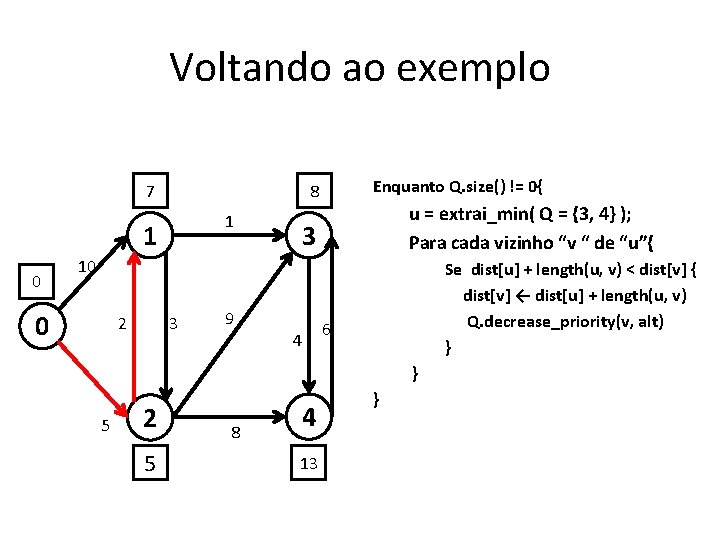
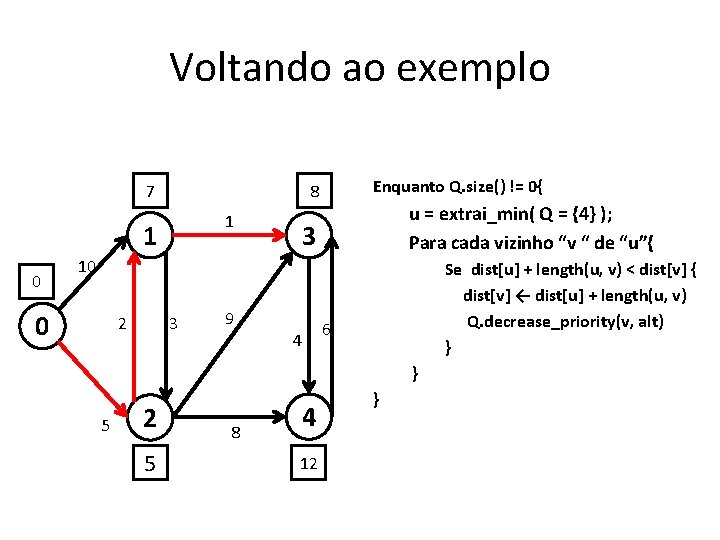
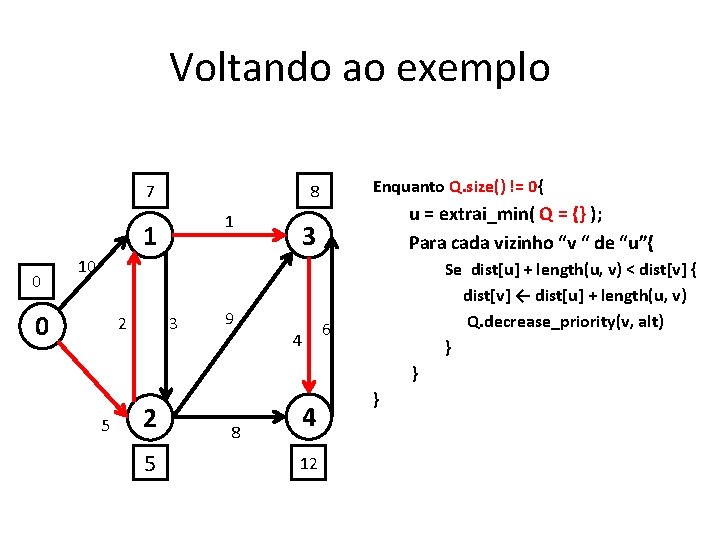
Funcionamento • Enquanto Q. size() != 0{ u = extrai_min( Q ); Para cada vizinho “v “ de “u”{ } } Se dist[u] + length(u, v) < dist[v] { dist[v] ← dist[u] + length(u, v) Q. decrease_priority(v, alt) } • A técnica de relaxamento para um arco (u, v) consiste em testar se é possível melhorar o caminho mais curto para v passando por u, e em caso afirmativo, atualizar dist[v].

Voltando ao exemplo ∞ 10 1 1 0 Enquanto Q. size() != 0{ u = extrai_min( Q = {2, 1, 3, 4} ); Para cada vizinho “v “ de “u”{ 3 10 0 2 3 9 4 Se dist[u] + length(u, v) < dist[v] { dist[v] ← dist[u] + length(u, v) Q. decrease_priority(v, alt) } 6 } 5 2 5 8 4 ∞ }

Voltando ao exemplo 7 14 1 1 0 Enquanto Q. size() != 0{ u = extrai_min( Q = {1, 4, 3} ); Para cada vizinho “v “ de “u”{ 3 10 0 2 3 9 4 Se dist[u] + length(u, v) < dist[v] { dist[v] ← dist[u] + length(u, v) Q. decrease_priority(v, alt) } 6 } 5 2 5 8 4 13 }

Voltando ao exemplo 7 1 1 0 Enquanto Q. size() != 0{ 8 u = extrai_min( Q = {3, 4} ); Para cada vizinho “v “ de “u”{ 3 10 0 2 3 9 4 Se dist[u] + length(u, v) < dist[v] { dist[v] ← dist[u] + length(u, v) Q. decrease_priority(v, alt) } 6 } 5 2 5 8 4 13 }

Voltando ao exemplo 7 1 1 0 Enquanto Q. size() != 0{ 8 u = extrai_min( Q = {4} ); Para cada vizinho “v “ de “u”{ 3 10 0 2 3 9 4 Se dist[u] + length(u, v) < dist[v] { dist[v] ← dist[u] + length(u, v) Q. decrease_priority(v, alt) } 6 } 5 2 5 8 4 12 }

Voltando ao exemplo 7 1 1 0 Enquanto Q. size() != 0{ 8 u = extrai_min( Q = {} ); Para cada vizinho “v “ de “u”{ 3 10 0 2 3 9 4 Se dist[u] + length(u, v) < dist[v] { dist[v] ← dist[u] + length(u, v) Q. decrease_priority(v, alt) } 6 } 5 2 5 8 4 12 }

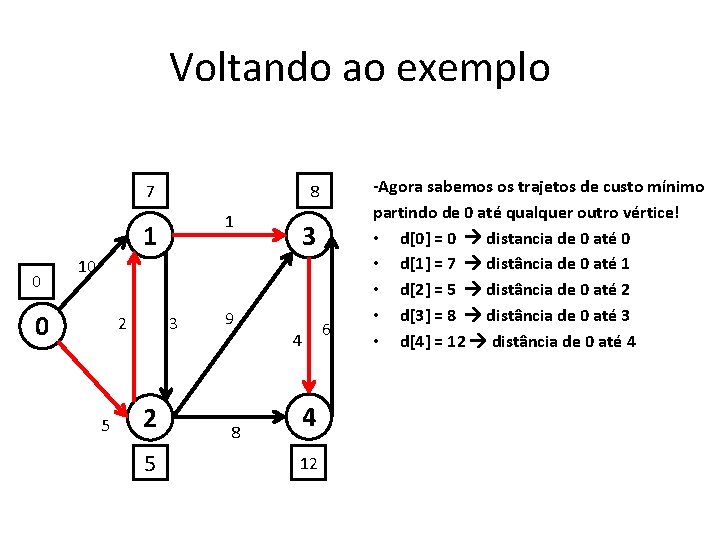
Voltando ao exemplo 7 8 1 1 0 3 10 0 2 5 3 2 5 9 8 4 4 12 6 -Agora sabemos os trajetos de custo mínimo partindo de 0 até qualquer outro vértice! • d[0] = 0 distancia de 0 até 0 • d[1] = 7 distância de 0 até 1 • d[2] = 5 distância de 0 até 2 • d[3] = 8 distância de 0 até 3 • d[4] = 12 distância de 0 até 4

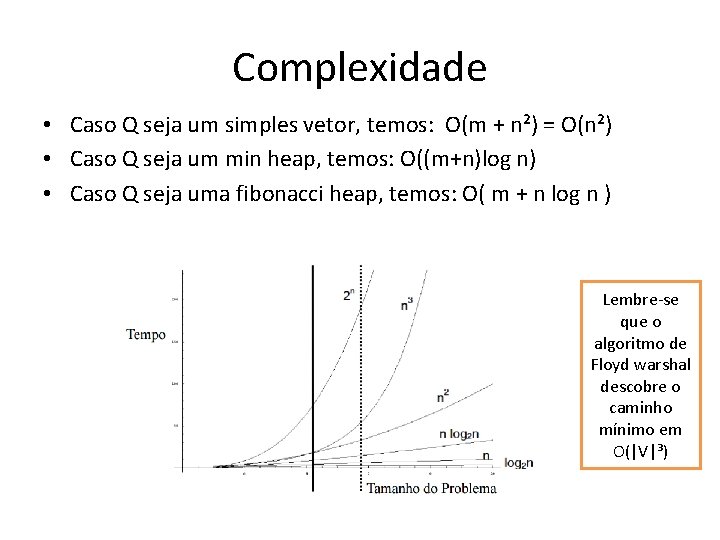
Complexidade • Para qualquer implementação do conjunto Q, o tempo de execução é: • O(|E|. Tdk + |V|. Tem) – Onde Tdk = complexidade das operações decrease_key – e Tem = complexidade das operações extract_minimum

Complexidade • Caso Q seja um simples vetor, temos: O(m + n²) = O(n²) • Caso Q seja um min heap, temos: O((m+n)log n) • Caso Q seja uma fibonacci heap, temos: O( m + n log n ) Lembre-se que o algoritmo de Floyd warshal descobre o caminho mínimo em O(|V|³)

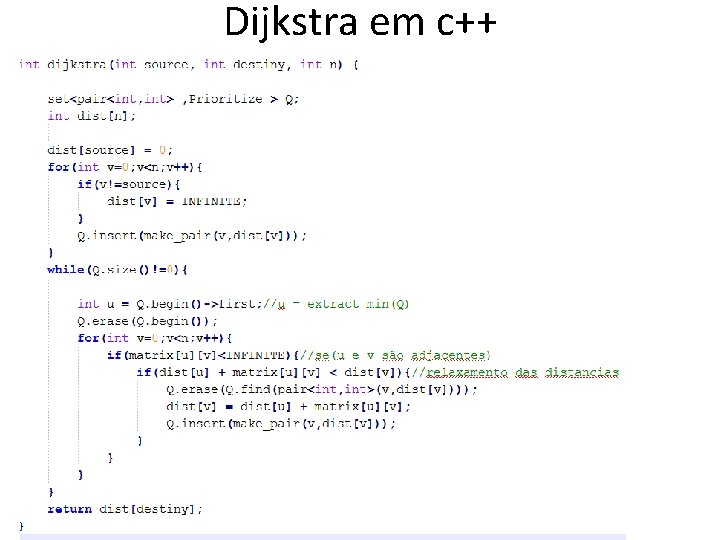
Dijkstra em c++

Exemplos de problemas que utilizam Dijkstra: • URI - 1148 – https: //www. urionlinejudge. com. br/judge/pt/problems/view/1148 • UVA - 929 – • http: //uva. onlinejudge. org/index. php? option=com_onlinejudge&Itemid=8&category=11&page=show_problem&problem=870 UVA - 10806 – http: //uva. onlinejudge. org/index. php? option=com_onlinejudge&Itemid=8&page=show_problem &problem=1747 • UVA - 11813 – http: //uva. onlinejudge. org/index. php? option=com_onlinejudge&Itemid=8&page=show_problem &problem=2913

FIM