Algoritmi si programare AP Dorel Lucanu http www

Algoritmi si programare (AP) Dorel Lucanu http: //www. infoiasi. ro/~dlucanu/

Obiective o o Algoritmi: n însuşirea unei gândiri algoritmice n dezvoltarea abilitaţilor de proiectare de soluţii algoritmice n însuşirea tehnicilor de utilizare a principalelor structuri de date n evaluarea timpului de execuţie in cazul cel mai nefavorabil Programare n iniţiere în utilizarea unui limbaj de programare n descrierea principalelor structuri de date n însuşirea tehnicilor de bază în proiectarea programelor Dorel Lucanu Algoritmica si programare

Agenda disciplina o o Algoritmi n Limbaj algoritmic, tablouri, structuri statice, structuri înlănţuite n liste liniare n arbori binari, heap-uri, union-find n grafuri (ca structuri de date) n sortare, căutare n paradigme Programare n prezentarea graduata a limbajului C (ISO Standard) cu accent pe implementarea structurilor de date si a soluţiilor prezentate in prima parte Dorel Lucanu Algoritmica si programare

Evaluare o o o conditii n activitatea la seminar (AS) n activitatea la laborator (AL) n testele scrise (TS) criterii de promovare n AS 5, AL 6, TS 4 forme n AS: întrebări, participare la discuţii, soluţii originale n AL: fiecare tema de laborator va fi notata cu note de la 10 n TS: 2 teste scrise (săpt. 7, 13), fiecare test conţinând 8 întrebări grilă şi o problemă. Dorel Lucanu Algoritmica si programare

Nota finala o o normele ECTS (European Credit Transfer System) Punctaj Final (PF) = 10% AS + 40% AL +50% TS 4 daca sunt indeplinite conditiile si NU sunt indeplinite criteriile de promovare, = 10 daca PF este in primii 10% din cei promovati (A) = 9 urmatorii 25% din cei promovati (B) = 8 urmatorii 30% din cei promovati (C) = 7 urmatorii 25% din cei promovati (D) = 6 urmatorii 10% din cei promovati (D) = 5 daca criteriile nu sunt indeplinite cu o eroare de 3% si activitatea generala justifica totusi o promovare la limita (max 5% din cei promovati) Dorel Lucanu Algoritmica si programare

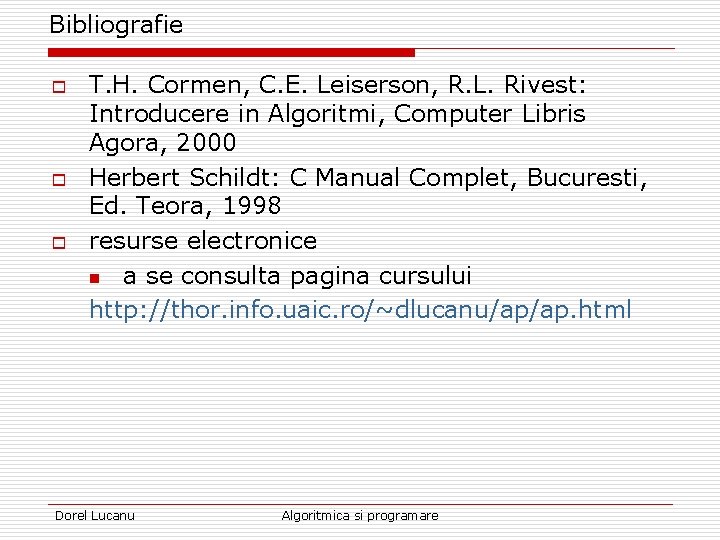
Bibliografie o o o T. H. Cormen, C. E. Leiserson, R. L. Rivest: Introducere in Algoritmi, Computer Libris Agora, 2000 Herbert Schildt: C Manual Complet, Bucuresti, Ed. Teora, 1998 resurse electronice n a se consulta pagina cursului http: //thor. info. uaic. ro/~dlucanu/ap/ap. html Dorel Lucanu Algoritmica si programare

Curs 1 - Agenda o o o limbaj algoritmic tablouri structuri calculul unui program problema rezolvata de un program timpul de executie Dorel Lucanu Algoritmica si programare

Algoritm o o algoritm = o secventa finita de pasi aranjata intr-o ordine logica specifica cu proprietatea ca, atunci cand este executata, produce o solutie corecta la o problema data. exemplu: reteta culinara algoritm calculator (“computer algorithm”) = un algoritm pentru care secventa de pasi este executata de un calculator limbaj algoritmic = un limbaj cu care sunt descrisi algoritmii Dorel Lucanu Algoritmica si programare

Tip de date: definitii o o o tip de date = colectie de entitati de tip data (obiecte reprezentabile in memoria calculatorului) si un set de operatii peste aceste obiecte tip de date abstract = tip de data organizat in asa fel incat specificarea obiectelor si specificarea operatiilor este independenta de reprezentarea obiectelor si implementarea operatiilor model standard = model utilizat pentru specificarea tipurilor de data abstracte (bazat pe notatii matematice) Dorel Lucanu Algoritmica si programare

Tip de date abstract: exemple o o INT n obiecte: int = {. . . – 2, – 1, 0, 1, 2, . . . } n operatii: o adunarea n intrare: a, b int n iesire: a + b o. . . BOOL n obiecte: bool = {false, true} n operatii: o conjunctia n intrare: a, b bool n iesire: a b (a and b) o. . . Dorel Lucanu Algoritmica si programare

Limbaj algoritmic o o o Dorel Lucanu modelarea memoriei tipuri de date elementare instructiuni tipuri de date structurate de nivel jos calcul timpul de executie Algoritmica si programare

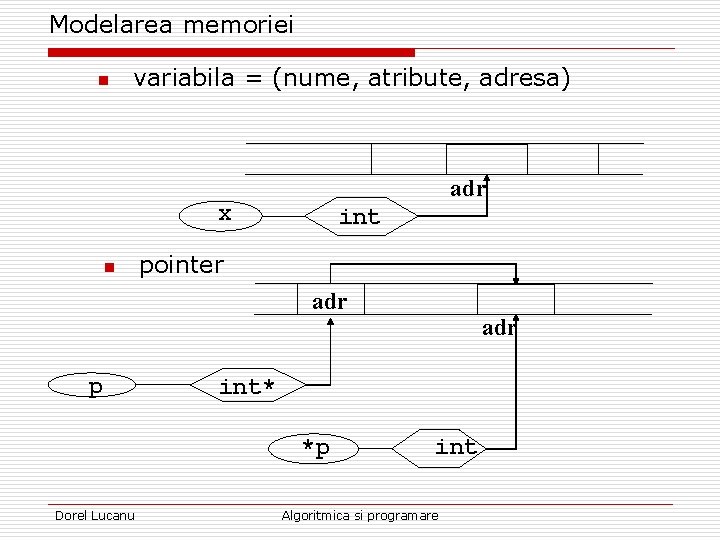
Modelarea memoriei n variabila = (nume, atribute, adresa) adr x n int pointer adr p int* *p Dorel Lucanu adr int Algoritmica si programare

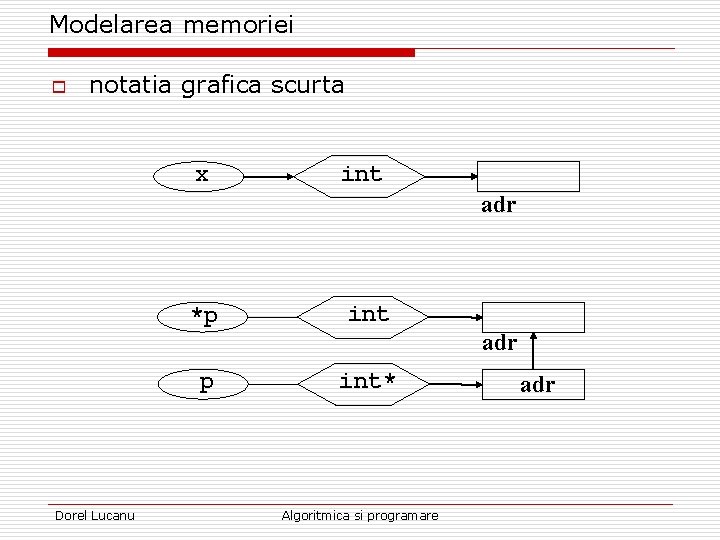
Modelarea memoriei o notatia grafica scurta x int adr Dorel Lucanu *p int* adr Algoritmica si programare adr

Tipuri de date elementare o o o numere intregi numere rationale valori booleene pointeri. . . Dorel Lucanu Algoritmica si programare

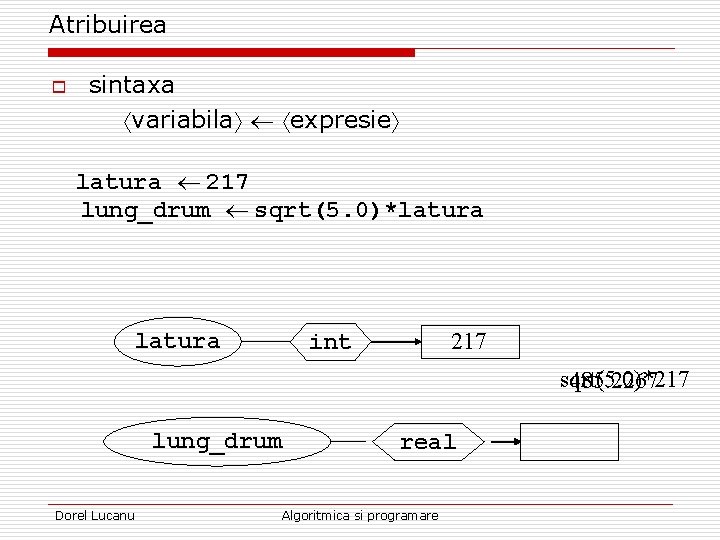
Atribuirea o sintaxa variabila expresie latura 217 lung_drum sqrt(5. 0)*latura 217 int sqrt(5. 0)*217 485. 2267 lung_drum Dorel Lucanu real Algoritmica si programare

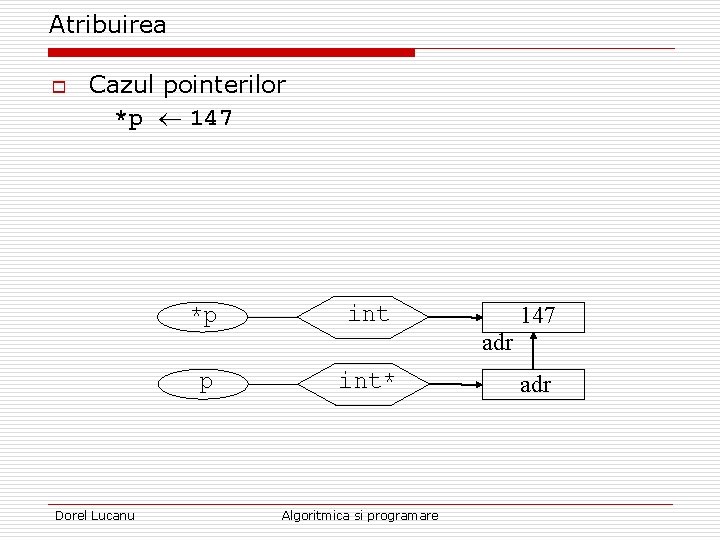
Atribuirea o Cazul pointerilor *p 147 Dorel Lucanu *p int* 147 adr Algoritmica si programare adr

if o o sintaxa if expresie then secventa_instructiuni else secventa_instructiuni semantica if e then i 1 else i 2 1. se evalueaza e 2. daca rezultatul este adevarat atunci executa i 1 altfel executa i 2 Dorel Lucanu Algoritmica si programare

if - exemple o o calcululul min(a, b) - varianta 1 if (a < b) then min a else min b calcululul min(a, b) - varianta 1 min a if (b < a) then min b Dorel Lucanu Algoritmica si programare

while o o sintaxa while ( expresie ) do secventa_instructiuni semantica while (e) do i 1. . . ik 1. se evalueaza e 2. daca rezultatul este adevarat a) se executa instructiunile i 1, . . . , ik b) se reia procesul de la pasul 1 3. altfel, executia instructiunii while se termina Dorel Lucanu Algoritmica si programare

while - exemple o cel mai mic k a. i. 7 k ≥ n pentru un n dat k 0 sapte_la_k 1 while (sapte_la_k < n) do k k+1 sapte_la_k * 7 Dorel Lucanu Algoritmica si programare

repeat o o sintaxa repeat secventa_instructiuni until expresie semantica repeat i 1. . . ik until (e) 1. se executa instructiunile i 1, . . . , ik 2. se evalueaza e 3. daca rezultatul este fals, se reia procesul de la pasul 1 4. altfel, executia instructiunii repeat se termina Dorel Lucanu Algoritmica si programare

repeat - exemple o o 7 k - inlocuirea lui while cu repeat k 0 sapte_la_k 1 repeat k k+1 sapte_la_k * 7 until (sapte_la_k n) pentru n = 0 nu mai obtinem rezultatul corect Dorel Lucanu Algoritmica si programare

for – versiunea 1 o o sintaxa for variabila expresie 1 to expresie 2 do secventa_instructiuni semantica for i e 1 to e 2 do i 1. . . ik Dorel Lucanu i e 1 while (i <= e 2) do i 1. . . ik i succ(i) Algoritmica si programare

for - exemple o o Exemplu: s = 1 + 2 +. . . + n s 0 for i 1 to n do s s + i Exemplu: a = 2 k a 1 for i 1 to k do a a * 2 Dorel Lucanu Algoritmica si programare

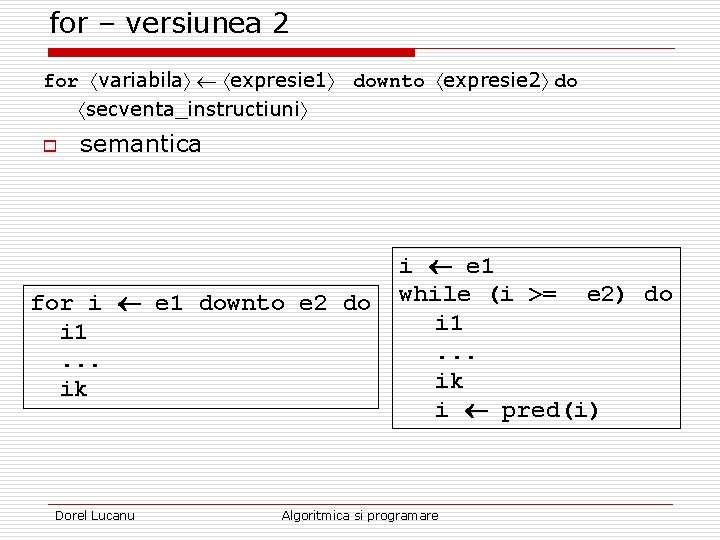
for – versiunea 2 for variabila expresie 1 downto expresie 2 do secventa_instructiuni o semantica for i e 1 downto e 2 do i 1. . . ik Dorel Lucanu i e 1 while (i >= e 2) do i 1. . . ik i pred(i) Algoritmica si programare

for - exemple o Exemplu: s = n + n-1 +. . . + 1 s 0 for i n downto 1 do s s + i Dorel Lucanu Algoritmica si programare

Subprograme - proceduri o sintaxa procedure nume ( parametri ) secventa_instructiuni end o clasificarea parametrilor: n de intrare n de iesire n de intrare/iesire Dorel Lucanu Algoritmica si programare

Subprograme - exemple o o interschimbarea valorilor a doua variabile procedure swap (a, b) temp a a b b temp end utilizare x 7 y 23 swap(x, y) // x = 23, y =7 Dorel Lucanu Algoritmica si programare

Subprograme - functii o o sintaxa function nume ( parametri ) secventa_instructiuni return expresie end pot exista mai multe instructiuni return Dorel Lucanu Algoritmica si programare

Subprograme - exemple o o functia care intoarce suma function suma(n) s 0 for i 1 to n do s s + i return s end utilizare v suma(m) – m/2 Dorel Lucanu Algoritmica si programare

Exceptii o o sintaxa throw mesaj if expresie then throw mesaj exemplu if (b = 0) then throw “impartire prin 0” x a/b Dorel Lucanu Algoritmica si programare

Calculul unui program x 1 i 2 while (i < 4) do x X*i i i+1 fiecare instructiune = o unitate de timpul de executie T=9 Dorel Lucanu pas Instruct. /exp x i 1 x 1 - - 2 i 2 1 - 3 i < 4 1 2 4 x x*i 1 2 5 i i+1 2 2 6 i < 4 2 3 7 x x*i 2 3 8 i i+1 6 3 9 i < 4 6 4 Algoritmica si programare

Calculul unui program o o o linie in tabel = configuratie (c) obtinerea unei linii din precedenta: relatie de tranzitie (ci-1 | ci) calcul problema calcul generat de instanta problema rezolvata de un program Dorel Lucanu Algoritmica si programare

Tablouri int a[3] a int[3] a[0] int a[1] int a[2] int a[1] 7 a[2] a[1] * 2 Dorel Lucanu Algoritmica si programare 7 14

Tablouri - exemple o o suma primelor n elemente dintr-un tablou s 0 for i 0 to n-1 do s s + a[i] cautarea unui element x intr-un tablou i 0 while (i < n-1 and a[i] != x) do i i + 1 if (a[i] = x) then poz i else poz -1 Dorel Lucanu Algoritmica si programare

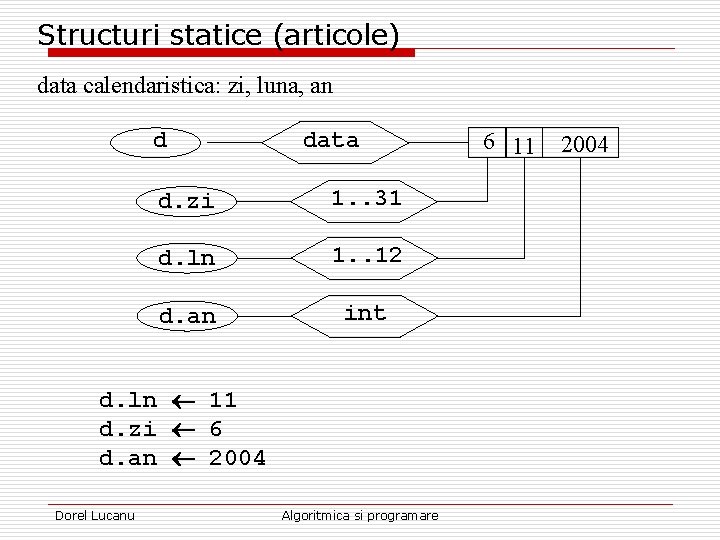
Structuri statice (articole) data calendaristica: zi, luna, an d data d. zi 1. . 31 d. ln 1. . 12 d. an int d. ln 11 d. zi 6 d. an 2004 Dorel Lucanu Algoritmica si programare 6 11 2004

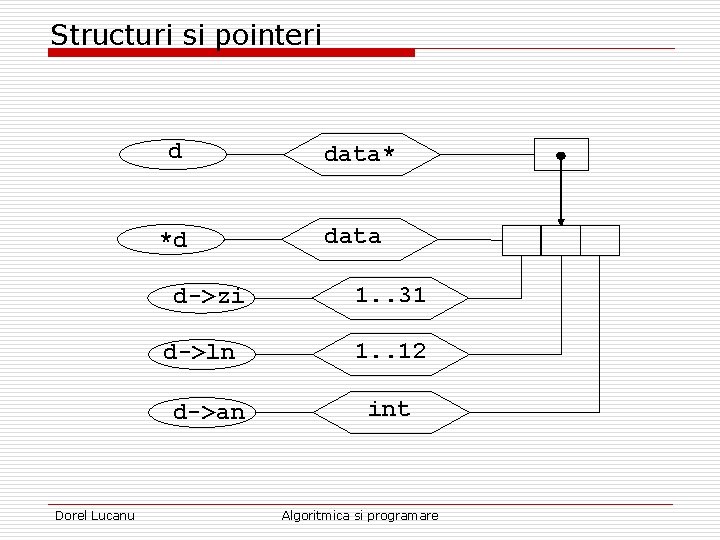
Structuri si pointeri d data* *d data d->zi d->ln d->an Dorel Lucanu 1. . 31 1. . 12 int Algoritmica si programare

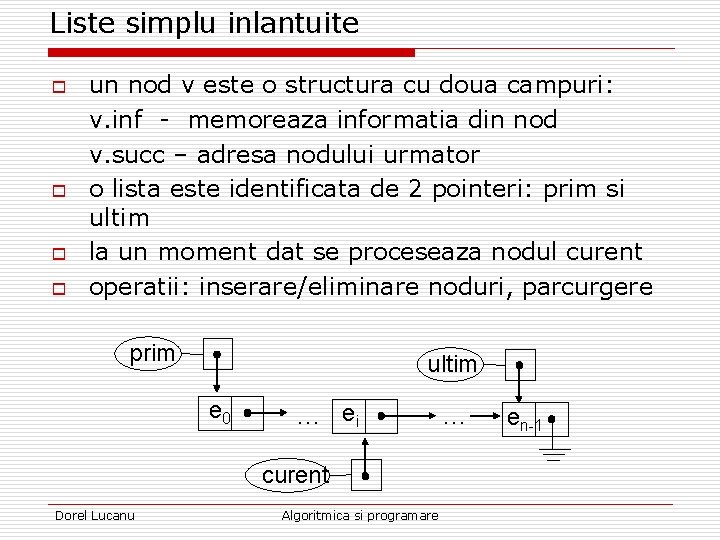
Liste simplu inlantuite o o un nod v este o structura cu doua campuri: v. inf - memoreaza informatia din nod v. succ – adresa nodului urmator o lista este identificata de 2 pointeri: prim si ultim la un moment dat se proceseaza nodul curent operatii: inserare/eliminare noduri, parcurgere prim ultim e 0 … ei curent Dorel Lucanu Algoritmica si programare … en-1

Timpul de executie in cazul cel mai nefavorabil i 0 while (i i i if (a[i] then poz else poz o o o < n-1 and a[i] != x) do + 1 = x) i -1 a = (4, 1, 5, 9, 6) daca x = 4, atunci T = 1 + 2 = 4 (cel mai favorabil) daca x = 6 sau x = 3, atunci T = 1 + 4*2 + 2 = 11 (cel mai nefavorabil) in general: T(n) = 1 + 2*(n-1) + 2 = 2*n+1 n – dimensiunea instantei problemei Dorel Lucanu Algoritmica si programare

Notatia O(f(n)) o o functii f(n) de argument numar natural si valori numere reale pozitive O(f(n)) = clasa functiilor marginite superior de f(n) n g(n) O(f(n)) daca exista c > 0, n 0 a. i. g(n) <= c*f(n) pentru orice n >= n 0 n functiile constante O(1) n polinoamele de grad 1 O(n) n polinoamele de grad 2 O(n 2) n functii logaritmice O(log n) Pentru cautarea in tablou: T(n) = O(n) notatie: T(n) = O(n) in loc de T(n) O(n) Dorel Lucanu Algoritmica si programare