ALGORITMI Osnovni elementi razvoja softvera Jasno definisanje problema

ALGORITMI
Osnovni elementi razvoja softvera ØJasno definisanje problema ØAnaliza problema ØRazvoj algoritma v. Koncepcija odozgo-nadole Ø Program – implementacija algoritma pisanjem instrukcija Ø Prevođenje programa Ø Testiranje ØIzrada programa dokumentacije

Algoritam n Algoritam je skup pravila formulisanih u cilju rešavanja određenog tipa zadatka Ø Algoritam se sastoji od niza algoritamskih koraka, čiji je redosled tačno utvrđen Ø Polazne veličine su ulazne veličine algoritma, a rešenja zadatka su izlazne veličine g Prikazivanje algoritma Ø Dijagramom toka ü Pregledan i lako čitljiv i za ljude koji ne znaju da programiraju ü Nezavisan od vrste računara i programskog jezika Ø Primenom ü Lakše pseudojezika je prevođenje u odgovarajuće programske instrukcije
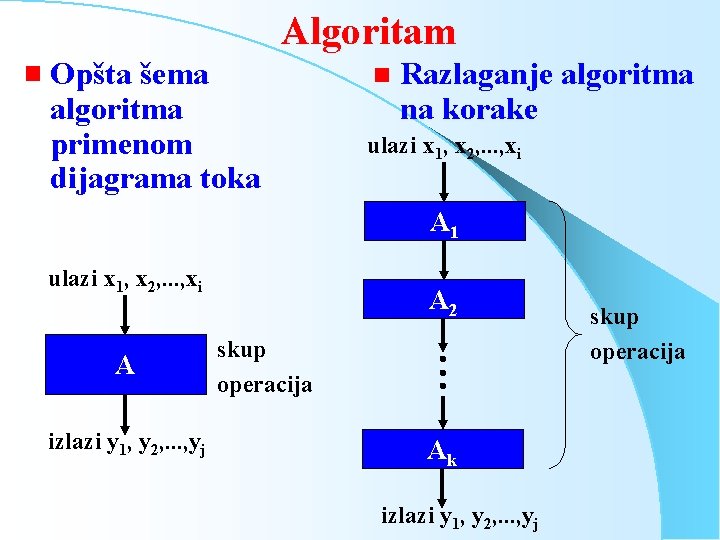
Algoritam g Opšta šema algoritma primenom dijagrama toka n Razlaganje algoritma na korake ulazi x 1, x 2, . . . , xi A 1 ulazi x 1, x 2, . . . , xi A izlazi y 1, y 2, . . . , yj A 2 skup operacija Ak izlazi y 1, y 2, . . . , yj skup operacija
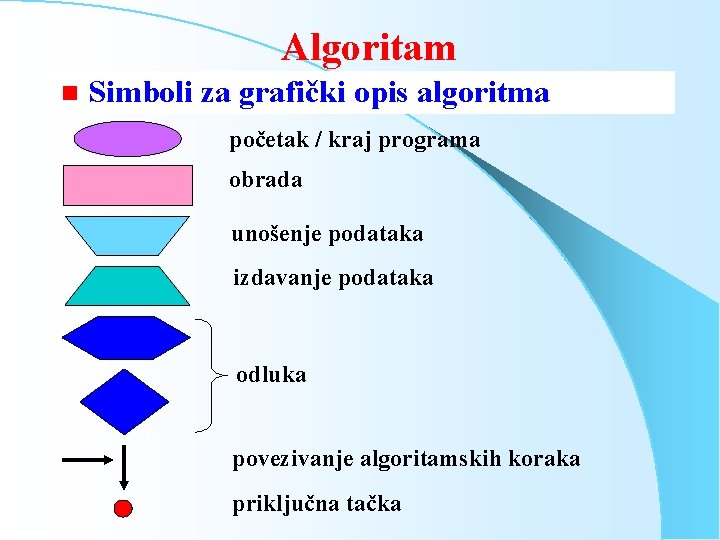
Algoritam n Simboli za grafički opis algoritma početak / kraj programa obrada unošenje podataka izdavanje podataka odluka povezivanje algoritamskih koraka priključna tačka

Algoritam n n Struktura algoritma je redosled izvršavanja algoritamskih koraka Osnovne kontrolne strukture: Ø Sekvence ü Proste linijske strukture Ø Selekcije ü Razgranate linijske strukture ü Skokovi (bezuslovni skokovi, višestruki skokovi) Ø Ciklične strukture (petlje) ü Uslovni ciklusi ü Brojački ciklusi ü Iterativni ciklusi g Svakoj kontrolnoj strukturi odgovara određena instrukcija u programskom jeziku
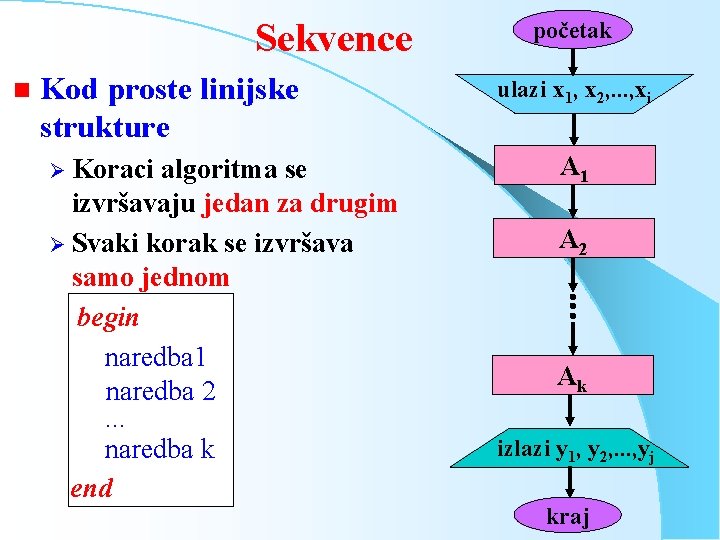
Sekvence n Kod proste linijske strukture Ø Koraci algoritma se izvršavaju jedan za drugim Ø Svaki korak se izvršava samo jednom begin naredba 1 naredba 2. . . naredba k end početak ulazi x 1, x 2, . . . , xi A 1 A 2 Ak izlazi y 1, y 2, . . . , yj kraj
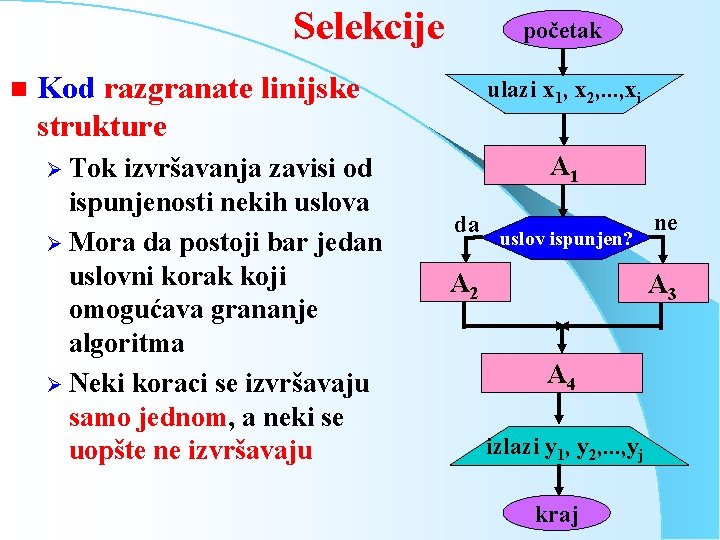
Selekcije n početak Kod razgranate linijske strukture izvršavanja zavisi od ispunjenosti nekih uslova Ø Mora da postoji bar jedan uslovni korak koji omogućava grananje algoritma Ø Neki koraci se izvršavaju samo jednom, a neki se uopšte ne izvršavaju ulazi x 1, x 2, . . . , xi A 1 Ø Tok da uslov ispunjen? A 2 ne A 3 A 4 izlazi y 1, y 2, . . . , yj kraj
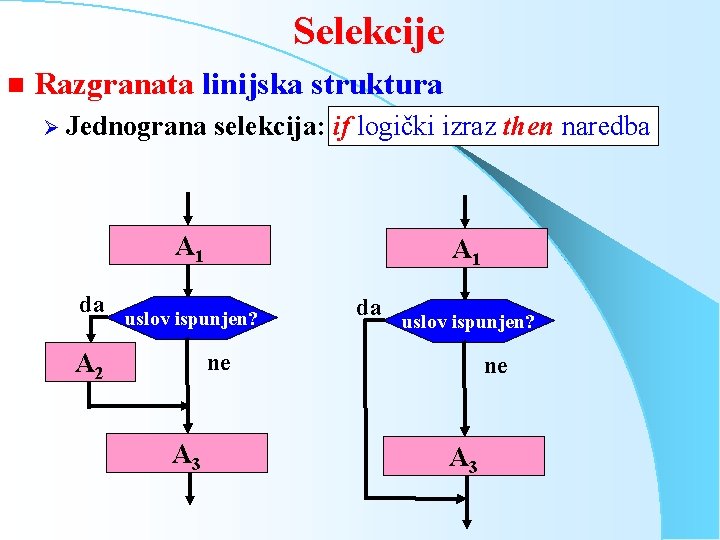
Selekcije n Razgranata linijska struktura Ø Jednograna selekcija: if logički izraz then naredba A 1 da A 1 uslov ispunjen? A 2 da uslov ispunjen? ne A 3
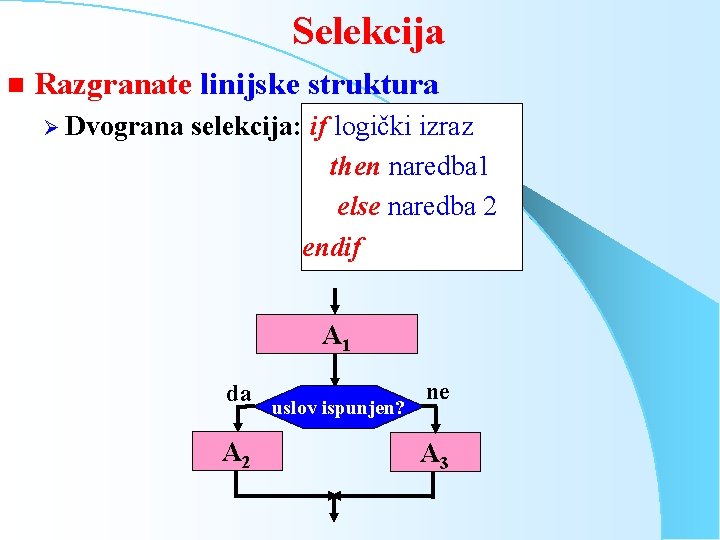
Selekcija n Razgranate linijske struktura Ø Dvograna selekcija: if logički izraz then naredba 1 else naredba 2 endif A 1 da A 2 uslov ispunjen? ne A 3

Selekcije n Skokovi mogu da budu uslovni i bezuslovni Ø Bezuslovnim skokovima se na nekom željenom mestu prekida obavljanje niza operacija, da bi se postupak obrade nastavio na nekom drugom zadatom mestu ü Dosledna primena pravila strukturnog programiranja eliminiše potrebu za bezuslovnim skokovima i zato u strukturnim dijagramima ne postoji poseban simbol za ovaj korak ü Primeri instrukcija za skok bilo gde unutar programa GO TO, BRANCH, JUMP ü Primer instrukcije za odlazak na kraj kontrolne strukture je EXIT, a za odlazak na kraj programa je STOP
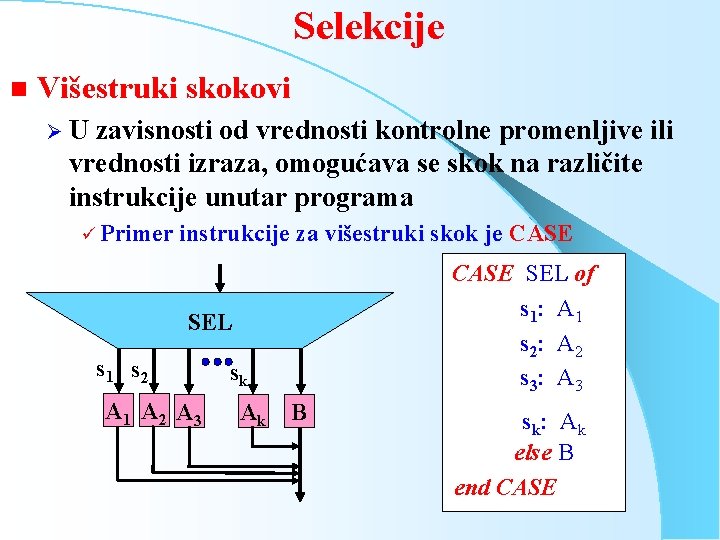
Selekcije n Višestruki skokovi ØU zavisnosti od vrednosti kontrolne promenljive ili vrednosti izraza, omogućava se skok na različite instrukcije unutar programa ü Primer instrukcije za višestruki skok je CASE SEL of s 1: A 1 s 2: A 2 s 3: A 3 SEL s 1 s 2 A 1 A 2 A 3 sk Ak B s k: A k else B end CASE

Ciklične strukture (petlje) n U cikličnoj strukturi (petlji) Ø Telo ciklusa čine naredbe čije se izvršavanje ponavlja pri jednom izvršavanju programa Ø Izlazni kriterijum ili uslov obezbeđuje prestanak izvršavanja ciklusa Kod ciklusa sa uslovom broj ponavljanja nije poznat unapred, već zavisi od ispunjenosti uslova g Kod brojačkih ciklusa kriterijum za izlazak iz petlje je broj ponovljenih ciklusa g Kod iterativnih ciklusa kriterijum za izlazak iz pelji je dostignuta tačnost izračunavanja g
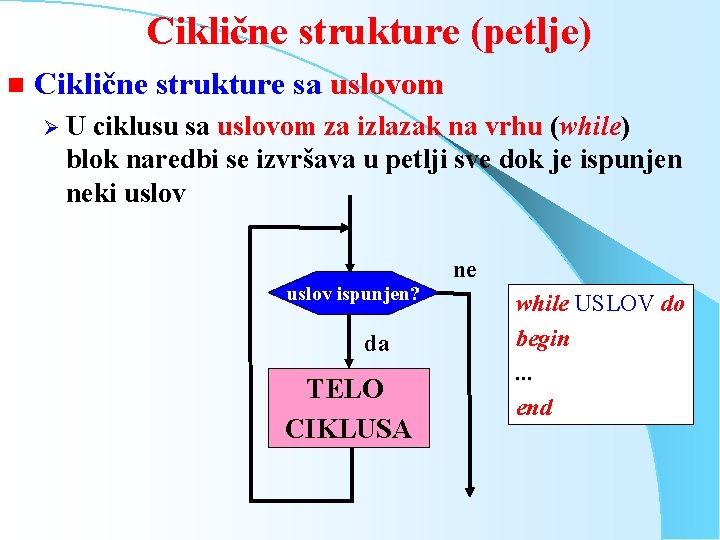
Ciklične strukture (petlje) n Ciklične strukture sa uslovom ØU ciklusu sa uslovom za izlazak na vrhu (while) blok naredbi se izvršava u petlji sve dok je ispunjen neki uslov ispunjen? da TELO CIKLUSA ne while USLOV do begin. . . end
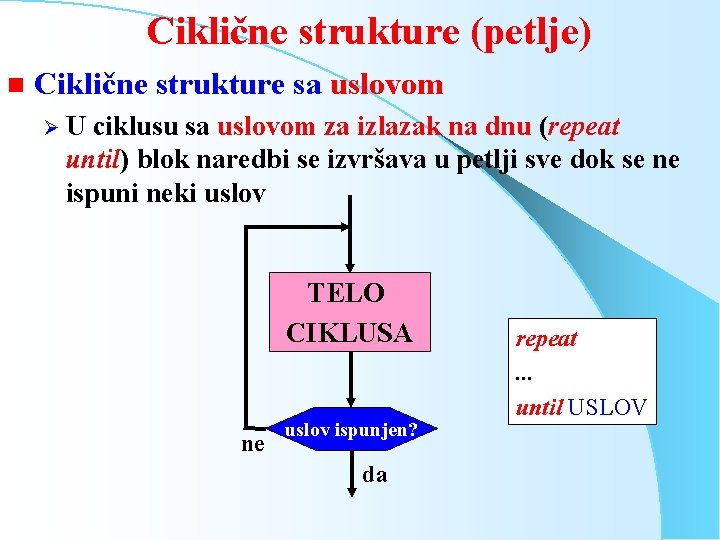
Ciklične strukture (petlje) n Ciklične strukture sa uslovom ØU ciklusu sa uslovom za izlazak na dnu (repeat until) blok naredbi se izvršava u petlji sve dok se ne ispuni neki uslov TELO CIKLUSA ne uslov ispunjen? da repeat. . . until USLOV

Ciklične strukture (petlje) n Elementi svakog brojačkog ciklusa (FOR) su: Ø Ø g g Brojač Početna vrednost brojača Krajnja vrednost brojača Korak brojača Na početku izvršavanja brojačkog ciklusa brojaču se dodeljuje početna vrednost Postoje brojački ciklusi sa brojanjem unapred i sa brojanjem unazad Vrednost brojača se sa svakim izvršavanjem ciklusa menja (uvećava ili smanjuje) za zadati korak Ciklus se završava kada brojač dostigne krajnju vrednost
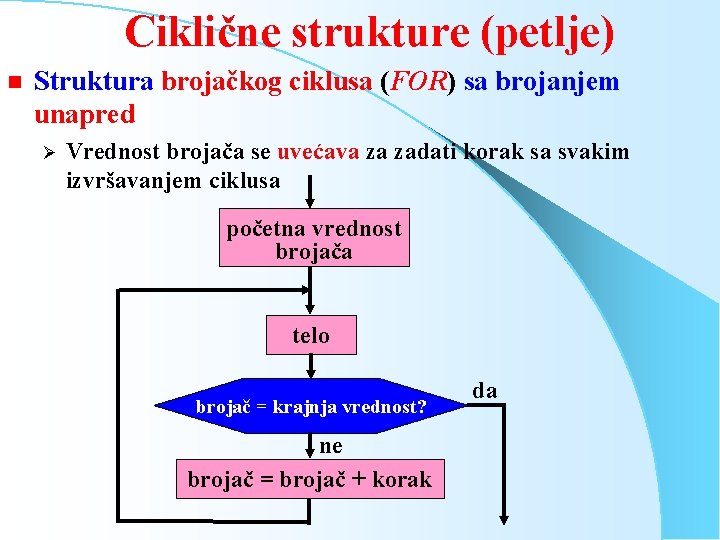
Ciklične strukture (petlje) n Struktura brojačkog ciklusa (FOR) sa brojanjem unapred Ø Vrednost brojača se uvećava za zadati korak sa svakim izvršavanjem ciklusa početna vrednost brojača telo brojač = krajnja vrednost? ne brojač = brojač + korak da

Ciklične strukture (petlje) n Struktura brojačkog ciklusa (FOR) sa brojanjem unazad Ø Vrednost brojača se umanjuje za zadati korak sa svakim izvršavanjem ciklusa početna vrednost brojača telo brojač = krajnja vrednost? ne brojač = brojač - korak da
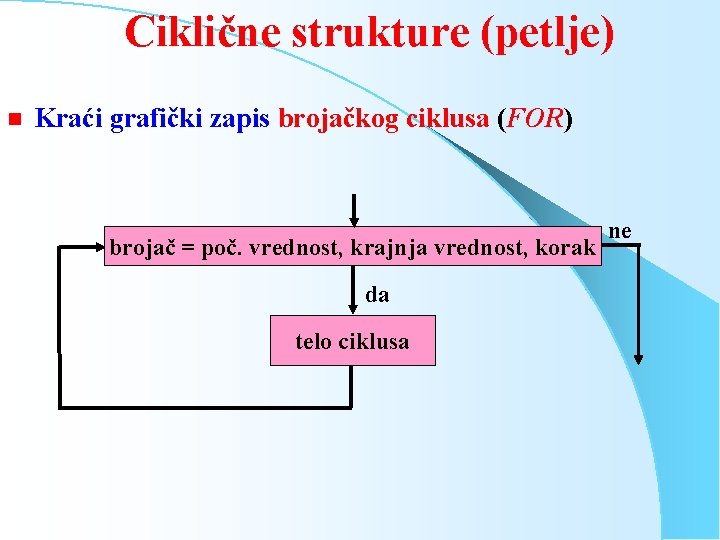
Ciklične strukture (petlje) n Kraći grafički zapis brojačkog ciklusa (FOR) brojač = poč. vrednost, krajnja vrednost, korak da telo ciklusa ne
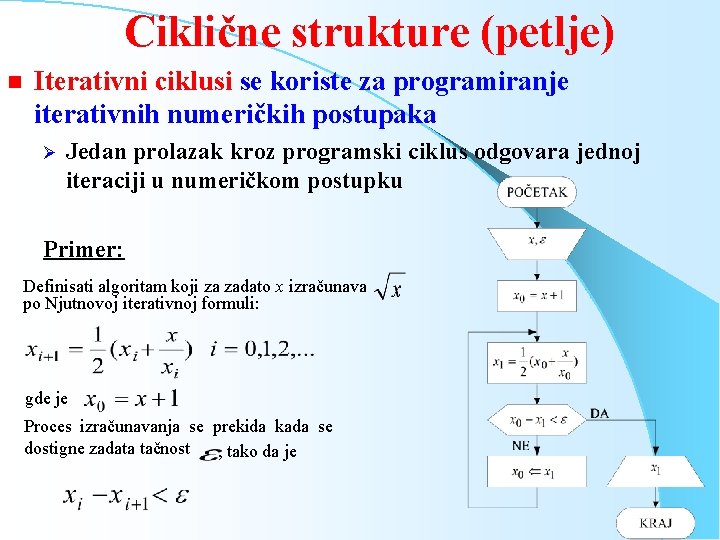
Ciklične strukture (petlje) n Iterativni ciklusi se koriste za programiranje iterativnih numeričkih postupaka Ø Jedan prolazak kroz programski ciklus odgovara jednoj iteraciji u numeričkom postupku Primer: Definisati algoritam koji za zadato x izračunava po Njutnovoj iterativnoj formuli: gde je Proces izračunavanja se prekida kada se dostigne zadata tačnost , tako da je.
- Slides: 20