Algoritmi e Strutture Dati Capitolo 4 Ordinamento Algoritmi

Algoritmi e Strutture Dati Capitolo 4 Ordinamento

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Richiamo: Delimitazione superiore alla complessità computazionale (temporale) di un algoritmo Ricorda: Un algoritmo A ha tempo di esecuzione T(n)=O(f(n)) su istanze di dimensione n se la quantità T(n) di tempo sufficiente per eseguire A su ogni istanza di dimensione n (e quindi in particolare anche nel caso peggiore) verifica la relazione T(n)=O(f(n)) Se scriverò che un algoritmo ha complessità T(n) = O(f(n)), intenderò che per ogni istanza più di quello non posso spendere. 2 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Richiamo: Delimitazione inferiore alla complessità computazionale (temporale) di un algoritmo Ricorda: Un algoritmo A ha tempo di esecuzione T(n)= (f(n)) su istanze di dimensione n se la quantità di tempo necessaria per eseguire A nel caso peggiore (e quindi non è detto che debba essere necessaria per ogni istanza di dimensione n: istanze facili potrebbero richiedere meno risorse!) verifica la relazione Tworst(n)= (f(n)) Convenzioni: 1. Se scriverò che un algoritmo ha complessità T(n) = O(f(n)), intenderò che su ALCUNE istanze costerà Θ(f(n)), ma sulle rimanenti costerà o(f(n) (esempio, l’IS). 2. Se scriverò che un algoritmo ha complessità T(n)=Θ(f(n)), intenderò che su TUTTE le istanze costerà Θ(f(n)) (esempio, il SS) 3 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Richiamo: Complessità computazionale di un problema Ricorda: (upper bound di un problema) Un problema P ha una delimitazione superiore alla complessità temporale O(f(n)) se esiste un algoritmo che risolve P il cui tempo di esecuzione è O(f(n)) Ricorda: (lower bound di un problema) Un problema P ha una delimitazione inferiore alla complessità temporale (complessità intrinseca) (f(n)) se ogni algoritmo (anche quelli non ancora progettati!) che risolverà P avrà almeno un’istanza con tempo di esecuzione (f(n)) 4 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Convenzione • Da ora in poi, quando parlerò di UB di un problema, mi riferirò alla complessità del MIGLIORE ALGORITMO che sono stato in grado di progettare sino a quel momento (ovvero, quello con minore complessità nel caso peggiore). • Da ora in poi, quando parlerò di LB di un problema, mi riferirò alla PIÙ GRANDE delimitazione inferiore che sono stato in grado di dimostrare sino a quel momento. 5 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Quindi, per il problema dell’ordinamento… • Upper bound temporale: O(n 2) – Insertion Sort, Selection Sort • Lower bound temporale: (n) – “banale”: dimensione dell’input Abbiamo un gap lineare tra upper bound e lower bound! Possiamo fare meglio? 6 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Ordinamento per confronti Dati due elementi ai ed aj, per determinarne l’ordinamento relativo effettuiamo una delle seguenti operazioni di confronto: ai aj ; ai aj Non si possono esaminare i valori degli elementi o ottenere informazioni sul loro ordine in altro modo. Notare: Tutti gli algoritmi di ordinamento considerati fino ad ora sono algoritmi di ordinamento per confronto. 7 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Lower bound (n log n) per l’ordinamento Consideriamo un generico algoritmo A, che ordina eseguendo solo confronti: dimostreremo che A esegue (nel caso peggiore) (n log n) confronti 8 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Gli algoritmi di ordinamento per confronto possono essere descritti in modo astratto in termini di alberi di decisione. Un generico algoritmo di ordinamento per confronto lavora nel modo seguente: - Confronta due elementi ai ed aj (ad esempio effettua il test ai aj); - A seconda del risultato – riordina e/o decide il confronto successivo da eseguire. Albero di decisione - Descrive i confronti che l’algoritmo esegue quando opera su un input di una determinata dimensione. I movimenti dei dati e tutti gli altri aspetti dell’algoritmo vengono ignorati 9 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

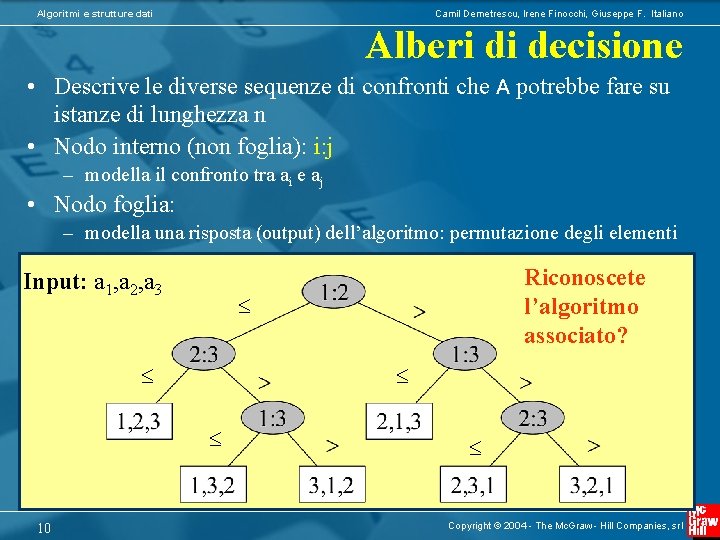
Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Alberi di decisione • Descrive le diverse sequenze di confronti che A potrebbe fare su istanze di lunghezza n • Nodo interno (non foglia): i: j – modella il confronto tra ai e aj • Nodo foglia: – modella una risposta (output) dell’algoritmo: permutazione degli elementi Input: a 1, a 2, a 3 10 Riconoscete l’algoritmo associato? Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Osservazioni • L’albero di decisione non è associato ad un problema • L’albero di decisione è associato ad un algoritmo e a una dimensione dell’istanza • L’albero di decisione descrive le diverse sequenze di confronti che un certo algoritmo può eseguire su istanze di una certa dimensione 11 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

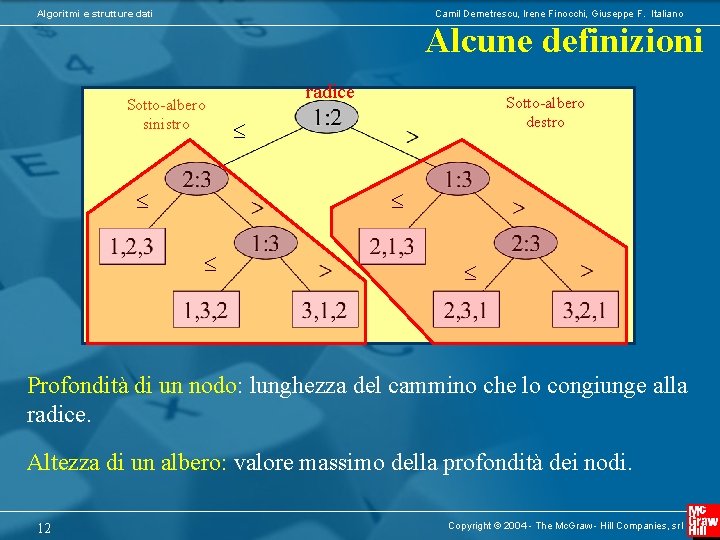
Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Alcune definizioni Sotto-albero sinistro radice Sotto-albero destro Profondità di un nodo: lunghezza del cammino che lo congiunge alla radice. Altezza di un albero: valore massimo della profondità dei nodi. 12 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Proprietà • Per una particolare istanza, i confronti eseguiti da A su quella istanza rappresentano un cammino radice – foglia • L’algoritmo segue un cammino diverso a seconda delle caratteristiche dell’input – Caso peggiore: cammino più lungo – Caso migliore: cammino più breve • Il numero di confronti nel caso peggiore è pari all’altezza dell’albero di decisione 13 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Altezza in funzione delle foglie Lemma: Un albero binario con k foglie in cui ogni nodo interno ha esattamente due figli, ha altezza h(k) log 2 k. Dim: Dimostrazione per induzione su k: – Caso base k=1: banale h(k)=0≥ log 21=0 – Caso k>1: supposto vero per k-1 foglie, dimostriamolo per k; poiché la radice ha 2 figli, almeno uno dei due suoi sottoalberi deve contenere almeno la metà (parte intera sup. ) delle foglie, e quindi h(k) ≥ 1+h( k/2 ) ≥ (hp induttiva) 1+log 2(k/2) =1+log 2 k-log 22=log 2 k. QED 14 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Il lower bound W(n log n) • Consideriamo l’albero di decisione di un qualsiasi algoritmo che risolve il problema dell’ordinamento di n elementi • L’altezza h(n) dell’albero di decisione è almeno log 2(n!): infatti, se l’algoritmo è corretto, deve contemplare tutti i possibili output, ovvero le n! permutazioni della sequenza di n elementi in input, e quindi deve avere almeno n! foglie h(n) log 2(n!) > log 2 (n/e)n = Formula di Stirling: n! (2 pn)1/2 ·(n/e)n > (n/e)n 15 = n log 2 (n/e) = = n log 2 n – n log 2 e = = (n log n) QED Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Un algoritmo ottimo: il Merge. Sort • Problema dell’ordinamento: – Lower bound - (n log n) albero di decisione – Upper bound – O(n 2) IS, SS • Proviamo a costruire un algoritmo ottimo, usando la tecnica del divide et impera: 1 Divide: dividi l’array a metà 2 Risolvi il sottoproblema ricorsivamente 3 Impera: fondi le due sottosequenze ordinate 16 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Esempio di esecuzione Input ed output delle chiamate ricorsive 17 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Fusione di sequenze ordinate • Due array ordinati A e B possono essere fusi rapidamente: – estrai ripetutamente il minimo di A e B e copialo nell’array di output, finché A oppure B non diventa vuoto – copia gli elementi dell’array non ancora completamente svuotato alla fine dell’array di output Notazione: dato un array A e due indici x y, denotiamo con A[x; y] la porzione di A costituita da A[x], A[x+1], …, A[y] 18 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Algoritmo di fusione di sequenze ordinate Merge (A, i 1, f 2) 1. Sia X un array ausiliario di lunghezza f 2 -i 1+1 2. i=1 3. i 2=f 1+1 4. while (i 1 f 1 e i 2 f 2) do 5. if (A[i 1] A[i 2]) 6. then X[i]=A[i 1] 7. 8. 9. incrementa i e i 1 else X[i]=A[i 2] Osservazione: sto usando un array ausiliario incrementa i e i 2 10. if (i 1<f 1) then copia A[i 1; f 1] alla fine di X 11. else copia A[i 2; f 2] alla fine di X 12. copia X in A[i 1; f 2] 19 fonde A[i 1; f 1] e A[f 1+1; f 2] output in A[i 1; f 2] Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Lemma La procedure Merge fonde due sequenze ordinate di lunghezza n 1 e n 2 eseguendo al più n 1+ n 2 -1 confronti Dim: Ogni confronto “consuma” un elemento di A. Nel caso peggiore tutti gli elementi tranne l’ultimo sono aggiunti alla sequenza X tramite un confronto. Il numero totale di elementi è n 1+ n 2. Quindi il numero totale di confronti è n 1+ n 2 -1. QED Numero di confronti: C(n=n 1+ n 2)=O(n), ma anche C(n)=Ω(min{n 1, n 2}) Numero di operazioni (confronti + copie)? T(n)= (n 1+ n 2) 20 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

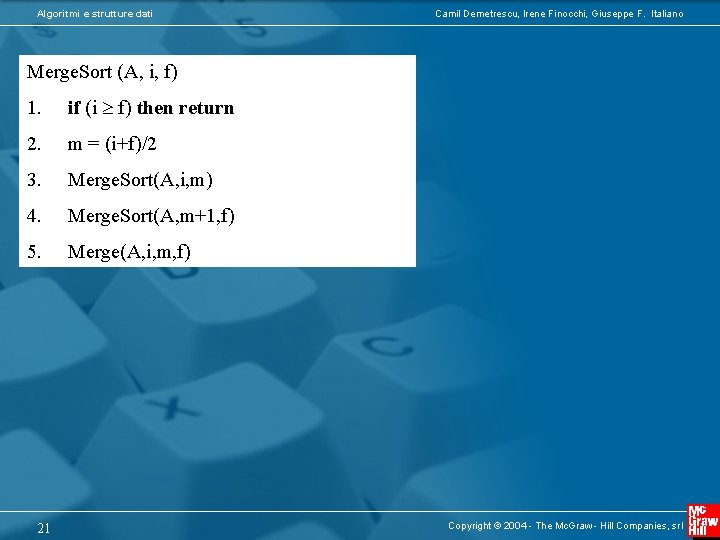
Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Merge. Sort (A, i, f) 1. if (i f) then return 2. m = (i+f)/2 3. Merge. Sort(A, i, m) 4. Merge. Sort(A, m+1, f) 5. Merge(A, i, m, f) 21 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Tempo di esecuzione • Il numero di confronti del Merge. Sort è descritto dalla seguente relazione di ricorrenza: C(n) = 2 C(n/2) + Θ(n) C(1)=1 (si noti che f(n)=Θ(n), in quanto il numero di confronti nelle fusioni è C(n)=O(n), ed anche C(n)=Ω(min{n 1, n 2})=Ω(min{n/2, n/2})=Ω(n)) • Usando il caso 2 del Teorema Master (infatti a=b=2, e quindi f(n)=Θ(nlog 22)), si ottiene C(n) = Θ(nlog 22 log n) = Θ(n log n) • Infine, per il tempo di esecuzione totale, si ha ancora: T(n) = 2 T(n/2) + Θ(n) T(1)=1 T(n) = Θ(n log n) 22 Copyright © 2004 - The Mc. Graw - Hill Companies, srl

Algoritmi e strutture dati Camil Demetrescu, Irene Finocchi, Giuseppe F. Italiano Osservazioni finali • Il Merge. Sort è un algoritmo (asintoticamente) ottimo rispetto al numero di confronti eseguiti nel caso peggiore • Il Merge. Sort non ordina in loco – occupazione di memoria pari a 2 n • Esercizio: costruire l’albero di decisione per il SS su una sequenza di 3 elementi. 23 Copyright © 2004 - The Mc. Graw - Hill Companies, srl