Algoritmi Cuprins l Capitolul I Noiunea de algoritm

Algoritmi

Cuprins l Capitolul I: Noţiunea de algoritm l Capitolul II: Caracteristicile algoritmilor l Capitolul III: Reprezentarea algoritmilor l Capitolul IV: Structura liniară l Capitolul V: Structura decizională l Capitolul VI: Structura repetitivă

Noţiunea de algoritm l l l Termenul de ALGORITM provine de la numele unui matematician persan, Abu Ja`far Mohammed ibn Musa al -Khowarizmi (al-Kwarizmi), ce a trait în secolul al IX-lea şi care a scris o lucrare despre efectuarea calculelor numerice într-o manieră algebrică. (“al-Khowarizmi” = din orasul Khowarizm) Prin algoritm se înţelege o metodă de soluţionare a unei clase de probleme, reprezentată de o succesiune finită de operaţii bine definite, numite instrucţiuni Prin algoritm vom înţelege o secvenţă finită de comenzi explicite şi neambigue care executate pentru o mulţime de date (ce satisfac anumite condiţii iniţiale) conduce în timp finit la rezultatul corespunzător. Primul algoritm se considera a algoritmul lui Euclid (utilizat pentru determinarea celui mare divizor comun a doua numere naturale). Termenul de algoritm poate fi înţeles în sens larg nefiind neapărat legat de rezolvarea unei probleme cu caracter ştiinţific, ci doar pentru a descrie într-o manieră ordonată activităţi care constau în parcurgerea unei succesiuni de paşi (cum este de exemplu utilizarea unui telefon public sau a unui bancomat).

Noţiunea de algoritm Etapele rezolvãrii unei probleme: Ø Ø Ø Analiza problemei Elaborarea unui algoritm Implementarea Verificarea corectitudinii Analiza complexitãþii algoritmului Orice algoritm lucreazã cu date, dupã cum urmeazã: üDate de intrare: datele pe care trebuie sã le primeascã un algoritm din exterior üDate de manevrã: date temporare, necesare algoritmului pentru a obţine rezultatele pe baza datelor de intrare üDate de ieşire: datele pe care trebuie sã le furnizeze algoritmul în exterior Datele cu care lucreazã algoritmii pot fi clasificate din mai multe puncte de vedere. - În funcţie de posibilitatea de a-şi modifica valoarea, datele sunt: o Constante: date care nu îşi modificã valoarea peparcursul algoritmului o Variabile: date care îşi modificã valoarea pe parcursul algoritmului - În funcţie de valoarea lor, datele sunt: o Date numerice: au ca valori numere Naturale Întregi Reale o Date alfabetice: au ca valori caractere sau şiruri de caractere o Date logice: au valoarea adevãrat sau fals.

Noţiunea de algoritm Etapele rezolvãrii unei probleme: Ø Ø Ø Analiza problemei Elaborarea unui algoritm Implementarea Verificarea corectitudinii Analiza complexitãþii algoritmului Orice algoritm lucreazã cu date, dupã cum urmeazã: üDate de intrare: datele pe care trebuie sã le primeascã un algoritm din exterior üDate de manevrã: date temporare, necesare algoritmului pentru a obţine rezultatele pe baza datelor de intrare üDate de ieşire: datele pe care trebuie sã le furnizeze algoritmul în exterior Datele cu care lucreazã algoritmii pot fi clasificate din mai multe puncte de vedere. - În funcţie de posibilitatea de a-şi modifica valoarea, datele sunt: o Constante: date care nu îşi modificã valoarea peparcursul algoritmului o Variabile: date care îşi modificã valoarea pe parcursul algoritmului - În funcţie de valoarea lor, datele sunt: o Date numerice: au ca valori numere Naturale Întregi Reale o Date alfabetice: au ca valori caractere sau şiruri de caractere o Date logice: au valoarea adevãrat sau fals.

Noţiunea de algoritm O expresie este constituiã dintr-o succesiune de operanzi, conectaţi prin operatori. Un operand poate fi o constantã, o variabilã sau o expresie încadratã între paranteze rotunde. Operatorii desemneazã operaþiile care se executã

Caracteristicile algoritmilor Generalitate. Un algoritm destinat rezolvării unei probleme trebuie să permită obţinerea rezultatului pentru orice date de intrare şi nu numai pentru date particulare de intrare. Finitudine. Adică se termină după un număr finit de paşi, indiferent cât de mulţi. Rigurozitate. Prelucrările algoritmului trebuie specificate riguros, fără ambiguităţi. În orice etapă a execuţiei algoritmului trebuie să se ştie exact care este următoarea etapă ce va executată. Eficienţă. Algoritmii pot fi efectiv utilizaţi doar dacă folosesc resurse de calcul în volum acceptabil. Prin resurse de calcul se înţelege volumul de memorie şi timpul necesar pentru execuţie.

Reprezentarea algoritmilor se poate realiza prin: Scheme logice Limbajul pseudocod Diagrame arborescente Tabele de decizie Schema logică este un mijloc de descriere a algoritmilor prin reprezentare grafică. Regulile de calcul ale algoritmului sunt descrise prin blocuri (figuri geometrice) reprezentând operaţiile (paşii) algoritmului, iar ordinea lor de aplicare (succesiunea operaţiilor) este indicată prin săgeţi. Fiecărui tip de operaţie îi este consacrată o figură geometrică (un bloc tip) în interiorul căreia se va înscrie operaţia din pasul respectiv. Limbajul Pseudocod este un limbaj inventat în scopul proiectării algoritmilor şi este format din propoziţii asemănătoare propoziţiilor limbii române, care corespund structurilor de calcul folosite în construirea algoritmilor.

Reprezentarea algoritmilor l l l Blocurile delimitatoare Start şi Stop (Fig. 1. 2. 1. a şi 1. 2. 1. b) vor marca începutul respectiv sfârşitul unui algoritm dat printr-o schemă logică. Descrierea unui algoritm prin schemă logică va începe cu un singur bloc Start şi se va termina cu cel puţin un bloc Stop. Blocurile de intrare/ieşire Citeşte şi Tipăreşte (Fig. 1. 2. 1. c şi d) indică introducerea unor Date de intrare respectiv extragerea unor Rezultate finale. Ele permit precizarea datelor iniţiale cunoscute în problemă şi tipărirea rezultatelor cerute de problemă. Blocul Citeşte iniţializează variabilele din lista de intrare cu valori corespunzătoare, iar blocul Tipăreşte va preciza rezultatele obţinute (la execuţia pe calculator cere afişarea pe ecran a valorilor expresiilor din lista de ieşire). Blocurile de atribuire (calcul) se utilizează în descrierea operaţiilor de atribuire (: =). Printr-o astfel de operaţie, unei variabile var i se atribuie valoarea calculată a unei expresii expr (Fig. 1. 2. 1. e).

Reprezentarea algoritmilor se poate realiza prin: Scheme logice Limbajul pseudocod Diagrame arborescente Tabele de decizie Schema logică este un mijloc de descriere a algoritmilor prin reprezentare grafică. Regulile de calcul ale algoritmului sunt descrise prin blocuri (figuri geometrice) reprezentând operaţiile (paşii) algoritmului, iar ordinea lor de aplicare (succesiunea operaţiilor) este indicată prin săgeţi. Fiecărui tip de operaţie îi este consacrată o figură geometrică (un bloc tip) în interiorul căreia se va înscrie operaţia din pasul respectiv. Limbajul Pseudocod este un limbaj inventat în scopul proiectării algoritmilor şi este format din propoziţii asemănătoare propoziţiilor limbii române, care corespund structurilor de calcul folosite în construirea algoritmilor.

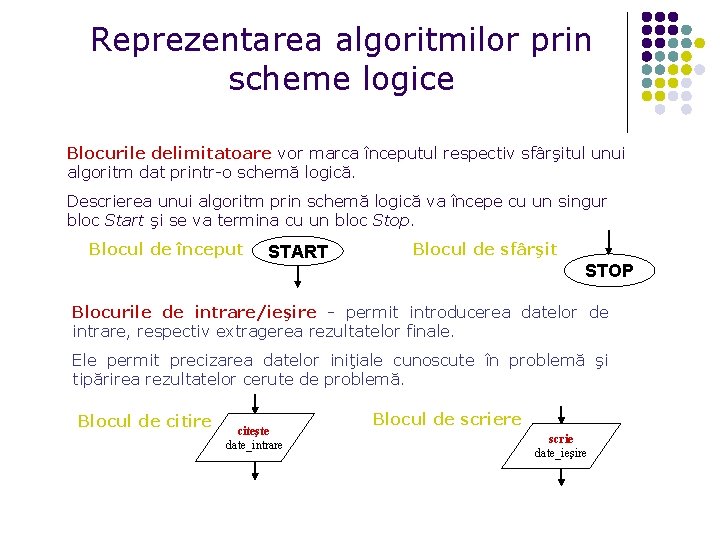
Reprezentarea algoritmilor prin scheme logice Blocurile delimitatoare vor marca începutul respectiv sfârşitul unui algoritm dat printr-o schemă logică. Descrierea unui algoritm prin schemă logică va începe cu un singur bloc Start şi se va termina cu un bloc Stop. Blocul de început START Blocul de sfârşit STOP Blocurile de intrare/ieşire - permit introducerea datelor de intrare, respectiv extragerea rezultatelor finale. Ele permit precizarea datelor iniţiale cunoscute în problemă şi tipărirea rezultatelor cerute de problemă. Blocul de citire citeşte date_intrare Blocul de scriere scrie date_ieşire

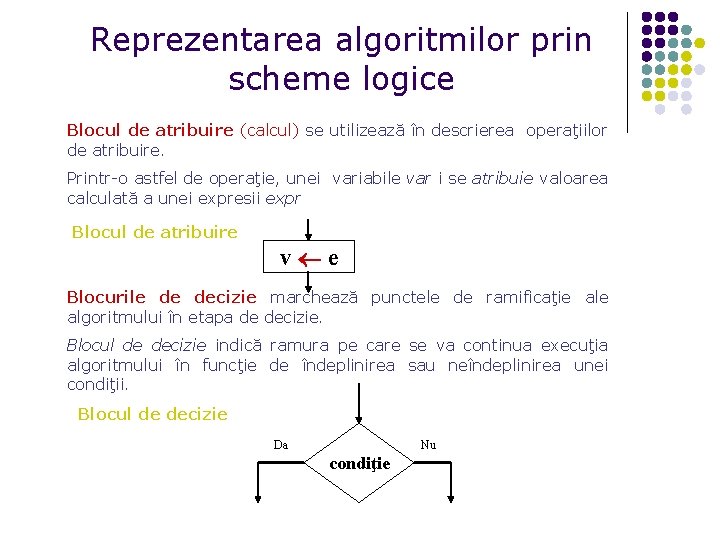
Reprezentarea algoritmilor prin scheme logice Blocul de atribuire (calcul) se utilizează în descrierea operaţiilor de atribuire. Printr-o astfel de operaţie, unei variabile var i se atribuie valoarea calculată a unei expresii expr Blocul de atribuire v e Blocurile de decizie marchează punctele de ramificaţie algoritmului în etapa de decizie. Blocul de decizie indică ramura pe care se va continua execuţia algoritmului în funcţie de îndeplinirea sau neîndeplinirea unei condiţii. Blocul de decizie Da Nu condiţie

Reprezentarea algoritmilor prin pseudocod Limbajul pseudocod este un limbaj situat între limbajul natural şi cel de programare. Este utilizat în scopul proiectării algoritmilor şi este format din propoziţii asemănătoare propoziţiilor limbii române, care corespund structurilor de calcul folosite în construirea algoritmilor. Pseudocod-ul conţine un set de cuvinte cheie. Un algoritm scris în pseudocod este de succesiune de instrucţiuni scrise în pseudocod. fapt o

Reprezentarea algoritmilor prin pseudocod Instrucţiunile pseudocodului sunt: Instrucţiunea de citire: citeste a, b; Instrucţiunea de scriere (afişare): scrie x ; Instrucţiunea de atribuire: x: =y+2; sau x y+2; Instrucţiunea decizională (alternativă): dacă condiţie atunci secvenţa_instrucţiuni_1 altfel secvenţa_instrucţiuni_2;

Reprezentarea algoritmilor prin pseudocod Instrucţiunea repetitivă cu număr necunoscut de paşi, condiţionată posterior: repetă secvenţă_instrucţiuni până când condiţie; Instrucţiunea repetitivă cu număr necunoscut de paşi, condiţionată anterior: cât timp condiţie execută secvenţă_instrucţiuni ; Instrucţiunea repetitivă cu număr cunoscut de paşi: pentru v = vin, vfin, [pas] execută secvenţă_instrucţiuni ;

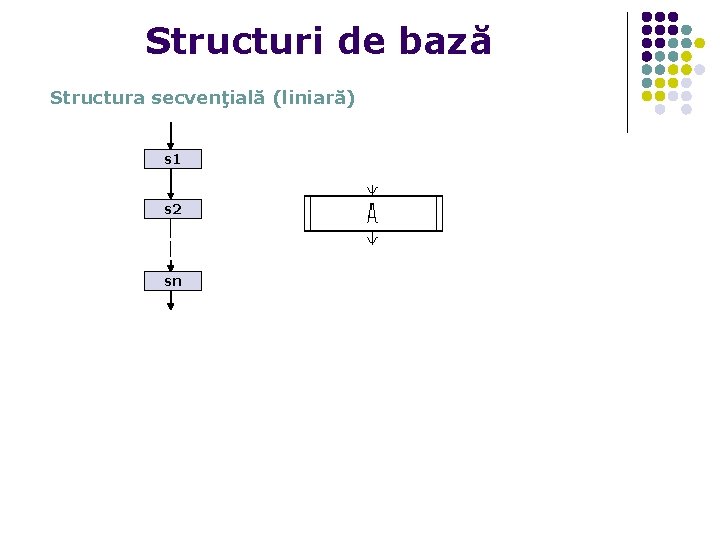
Structuri de bază Structura secvenţială (liniară) s 1 s 2 sn

Structura liniară Aplicaţie Se dă latura unui pătrat. Să se scrie algoritmul (schemă logică şi pseudocod) care să calculeze perimetrul şi aria pătratului. Comentarii: l Analizăm problema: ce se dă? Ce cunoaştem? Latura pătratului. Citim, deci, prin operaţia de citire, datele de intrare, în cazul nostru l. l Ce se cere? Perimetrul şi aria pătratului. Aici ne sare în ajutor matematica. Ştim că perimetrul unui pătrat este egal cu de 4 ori latura acestuia. Calculăm, deci, perimetrul cu ajutorul formulei şi atribuim variabilei P valoarea acestei expresii: P: =l*4. Un alt rezultat cerut este aria. Şi aceasta o putem calcula dacă ştim latura pătratului. Este egală cu latura*latura. Deci atribuim variabilei A expresia rezultată în urma calculului A: =l*l. l Rezulatele sunt P şi A. Le vom afişa la ecranul calculatorului în urma operaţei de scriere: scrie P, A Pseudocodul: l l Citeşte l P: =I*4 A: =l*l Scrie P, A START Citeşte l P: =l*4 A: =l*l Scrie P, A STOP

Structura liniară Probleme propuse l l Să se calculeze perimetrul unui triunghi, cunoscând cele trei laturi ale triunghiului, a, b, c. Perimetrul unui pătrat este egal cu latura altui pătrat. Ştiind că suma perimetrelor este x, să se calculeze ariile celor două pătrate. Se cunoaşte perimetrul unui pătrat. Să se scrie schema logică şi pseudocodul prin care putem afla latura pătratului. Se dau lungimea şi lăţimea unui dreptunghi. Să se calculeze perimetrul şi aria acestuia.

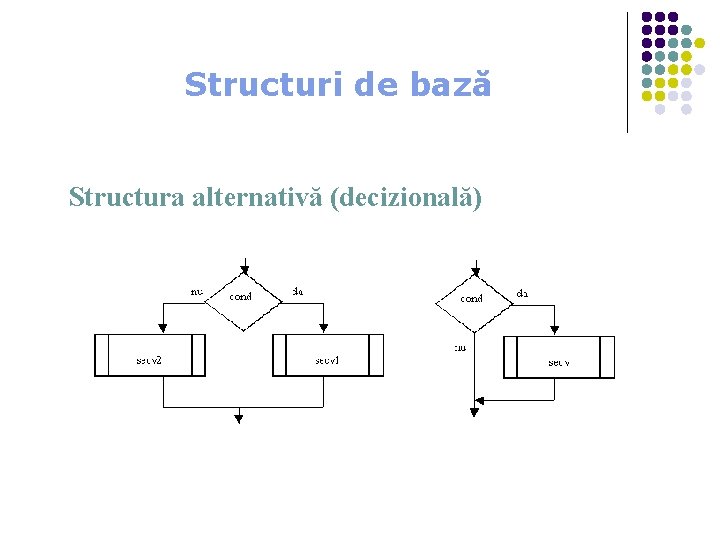
Structuri de bază Structura alternativă (decizională)

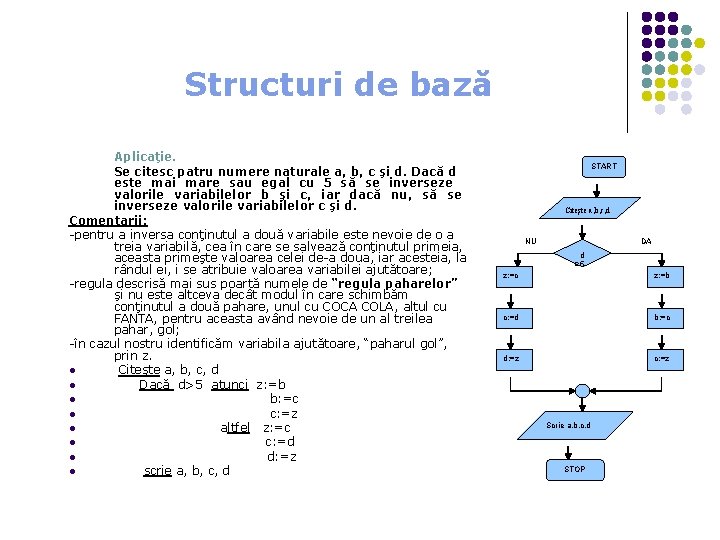
Structuri de bază Aplicaţie. Se citesc patru numere naturale a, b, c şi d. Dacă d este mai mare sau egal cu 5 să se inverseze valorile variabilelor b şi c, iar dacă nu, să se inverseze valorile variabilelor c şi d. Comentarii: -pentru a inversa conţinutul a două variabile este nevoie de o a treia variabilă, cea în care se salvează conţinutul primeia, aceasta primeşte valoarea celei de-a doua, iar acesteia, la rândul ei, i se atribuie valoarea variabilei ajutătoare; -regula descrisă mai sus poartă numele de “regula paharelor” şi nu este altceva decât modul în care schimbăm conţinutul a două pahare, unul cu COCA COLA, altul cu FANTA, pentru aceasta având nevoie de un al treilea pahar, gol; -în cazul nostru identificăm variabila ajutătoare, “paharul gol”, prin z. l Citeşte a, b, c, d l Dacă d>5 atunci z: =b l b: =c l c: =z l altfel z: =c l c: =d l d: =z l scrie a, b, c, d START Citeşte a, b, c, d NU DA d ≥ 5 z: =c z: =b c: =d b: =c d: =z c: =z Scrie a, b, c, d STOP

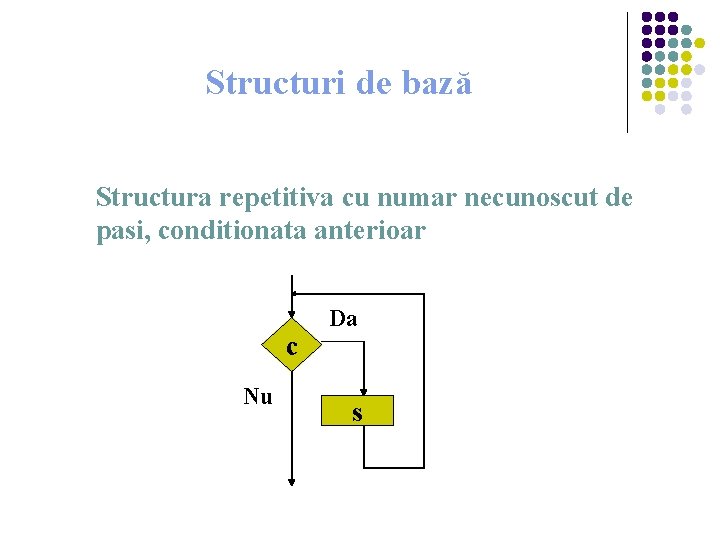
Structuri de bază Structura repetitiva cu numar necunoscut de pasi, conditionata anterioar c Nu Da s

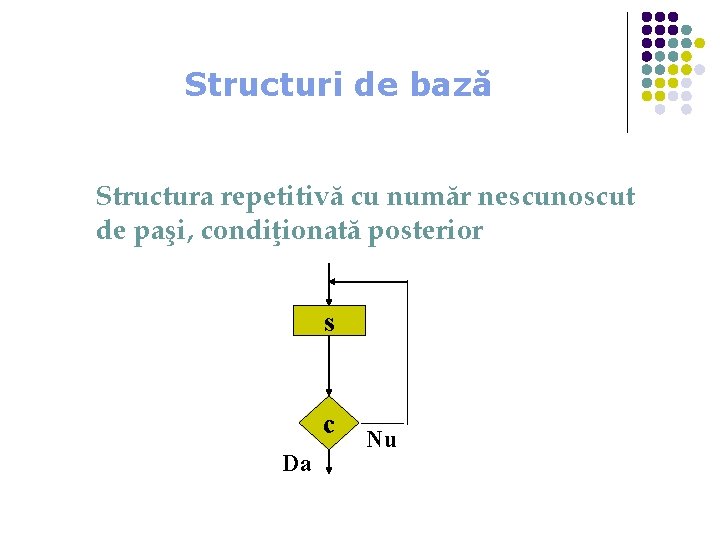
Structuri de bază Structura repetitivă cu număr nescunoscut de paşi, condiţionată posterior s c Da Nu

Structuri de bază Structura repetitiva cu un numar cunoscut de pasi v=vi v vf Nu Da s v=v+vr

Paşii realizării unui algoritm 1. Citirea cu atenţie a enunţului problemei. 2. Identificarea datelor de intrare şi a celor de ieşire. 3. Rezolvarea propriu-zisă a problemei pe cazuri particulare şi reprezentative. În acest moment nu se încearcă scrierea programului ci doar determinarea metodei de rezolvare, generalizarea şi înţelegerea acesteia. 4. Descrierea în limbaj natural a soluţiei problemei. Dacă nu sunteţi capabili să descrieţi metoda folosită în limbaj natural e puţin probabil să o puteţi face într-un limbaj de programare care e mai restrictiv decât limbajul natural. 5. Scrierea algoritmului. 6. Testarea algoritmului. Testarea se face pe mai multe seturi de date care să acopere cazurile posibile ce pot apărea.

Probleme şi condiţii 1. Nu orice problemă poate rezolvată algoritmic. a. Fiind dat un număr n să se determine toţi divizorii săi. Pentru această problemă se poate scrie un algoritm foarte uşor. b. Fiind dat un număr n să se determine toţi multiplii săi. Pentru această problemă nu se poate scrie un algoritm deoarece nu cunoaştem un criteriu de oprire a operaţiilor. 2. Un algoritm trebuie să funcţioneze pentru orice date de intrare. Fiind date numerele a, b, c să se afişeze maximul dintre ele. O posibilă soluţie ar fi: se compară a cu b şi c şi dacă e mai mare se afişează a, iar apoi se compară b cu a şi c şi dacă e mai mare se afişează b, iar apoi se compară c cu b şi a şi dacă e mai mare se afişează c Algoritmul nu funcţionează dacă 2 valori sunt identice şi de valoare maximă!

Probleme şi condiţii 3. Un algoritm trebuie sa se oprească. Se consideră următoarea secvenţă de prelucrări: Pas 1. Atribuie variabilei x valoarea 1; Pas 2. Măreste valoarea lui x cu 2; Pas 3. Daca x este egal cu 100 atunci se opreşte prelucrarea altfel se reia de la Pas 2. Este usor de observat ca x nu va lua niciodată valoarea 100, deci succesiunea de prelucrări nu se termină niciodată. Din acest motiv nu poate considerată un algoritm corect. 4. Prelucrările dintr-un algoritm trebuie să fie neambigue. Consideram următoarea secvenţă de prelucrări: Pas 1. Atribuie variabilei x valoarea 0; Pas 2. Fie se măreşte x cu 1 fie se micşorează x cu 1; Pas 3. Daca x aparţine [-10; 10] se reia de la Pas 2, altfel se opreşte algoritmul.

Probleme şi condiţii 5. Un algoritm trebuie să se oprească după un interval rezonabil de timp. Fiind dat un număr n se cere să se determine de câte ori a apărut o cifră c în reprezentarea tuturor numerelor naturale mai mici ca n. O rezolvare simplă ar fi să luăm toate numere mai mici ca n şi să vedem de câte ori apare cifra c în fiecare dinte ele. Soluţia e simplă şi pentru valori mici ale lui n algoritmul se termină într-un interval de timp rezonabil, dar pentru valori mari timpul de terminare al algoritmului creşte nepermis de mult.