ALGORITMA GRAF 1 Ada dua jenis algoritma dalam

ALGORITMA GRAF 1

Ada dua jenis algoritma dalam bab ini, yaitu : a. Algoritma Kruskal Algoritma ini digunakan untuk menentukan pohon perentang terbobot minimum. b. Algoritma Dijkstra Algoritma ini digunakan untuk menentukan lintasan terpendek pada graf berbobot. 2

Algoritma Kruskal : 1. Pilih busur e 1 sehingga bobot w(e 1) yang paling kecil. 2. Jika busur e 1, e 2, . . . , ek telah terpilih, pilih busur ek+1 dari busur yang belum dipilih sedemikian hingga (i) ek+1 tidak menjadi siklus di G dengan busur e 1, e 2, . . . , ek (ii) w(ek+1) sekecil mungkin berhubungan dengan (i) 3. Berhenti ketika langkah 2 tidak dapat dilanjutkan lagi. 3

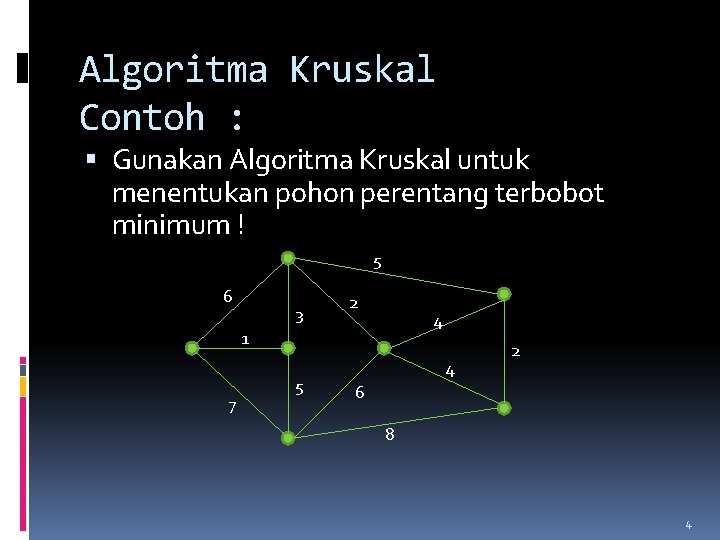
Algoritma Kruskal Contoh : Gunakan Algoritma Kruskal untuk menentukan pohon perentang terbobot minimum ! 5 6 3 2 4 1 7 5 4 2 6 8 4

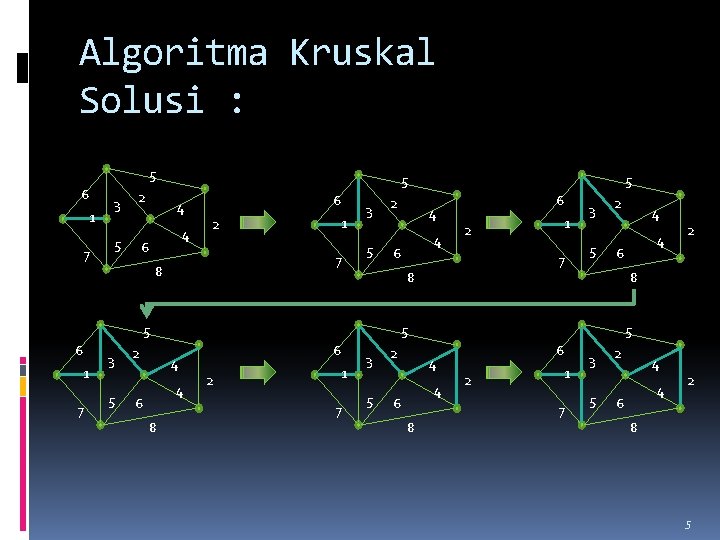
Algoritma Kruskal Solusi : 5 6 1 7 3 2 5 5 4 4 6 6 1 2 7 8 3 5 2 1 7 3 5 2 4 8 4 6 1 2 7 8 3 5 2 6 2 1 7 3 5 2 4 8 4 2 8 5 4 6 4 6 5 6 2 1 7 3 5 2 4 4 6 2 8 5

hasil 3 1 2 4 2 5 Bobot dari minimal spanning tree adalah : 17 6

Lintasan Terpendek • Lintasan terpendek dapat diartikan sebagai bobot minimal dari suatu lintasan, yaitu jumlah bobot dari seluruh busur yang membentuk lintasan. • Hanya terdapat satu bobot lintasan yang memenuhi, sedangkan lintasannya sendiri dapat lebih dari satu dengan bobot yang sama. • Ada beberapa metode yang dapat digunakan untuk menentukan lintasan terpendek, yaitu metode Dijkstra, Moore, Bellman, Matriks, dan Ford 7

Terminologi & Asumsi Length merupakan jumlah bobot dari lintasan, sedangkan bobot minimum dari lintasan (u, v) disebut distance d(u, v). Bobot minimum lintasan disebut lintasan terpendek. Jika eЄ E(G) maka w(e) = ∞ Asumsi mencari lintasan terpendek yaitu : 1. G merupakan graf simpel 2. Semua bobot di G positif 8

Algoritma Dijkstra : 1. Tentukan u 0 paling kiri. Biasanya u 0 diberi tahu. 2. Lintasan berakhir paling ujung. 3. Lintasan atau busur yang dilalui tidak boleh membentuk cycle. 4. Harus berurutan pemberian labelnya pada tiap simpul. 5. Carilah busur dengan bobot yang paling minimum. 9

Algoritma Dijkstra 1. [inisialisasi] Ambil L(a)=0. untuk semua vertex x≠a, buat L(x)=∞. Ambil T sebagai himpunan Vertex. 2. Bila z Є T, stop (L(z) adalah panjang dari path terpendek dari a ke z) 3. Pilih v Є T dengan harga terkecil dari L(v). Tempatkan T=T-(v) 4. Untuk tiap-tiap vertex x Є T adjacent dengan v, buat L(x)=min(L(x), L(V)+W(v, x) 5. Kembali ke langkah 2 10

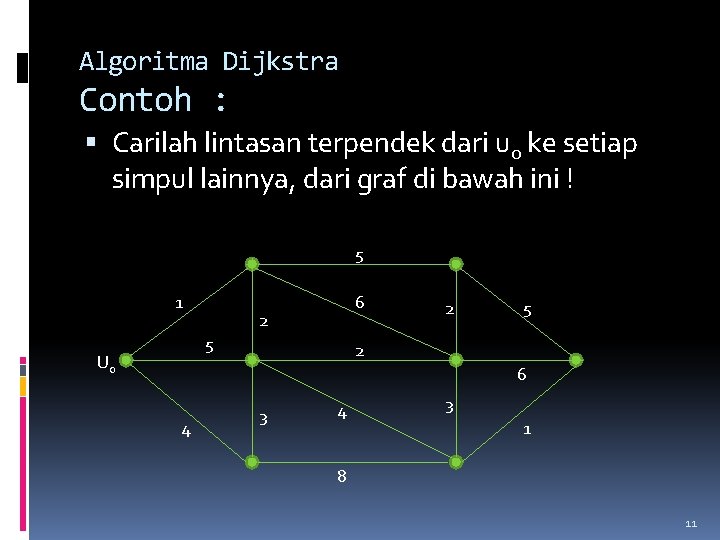
Algoritma Dijkstra Contoh : Carilah lintasan terpendek dari u 0 ke setiap simpul lainnya, dari graf di bawah ini ! 5 1 6 2 5 U 0 2 5 2 6 4 3 1 8 11

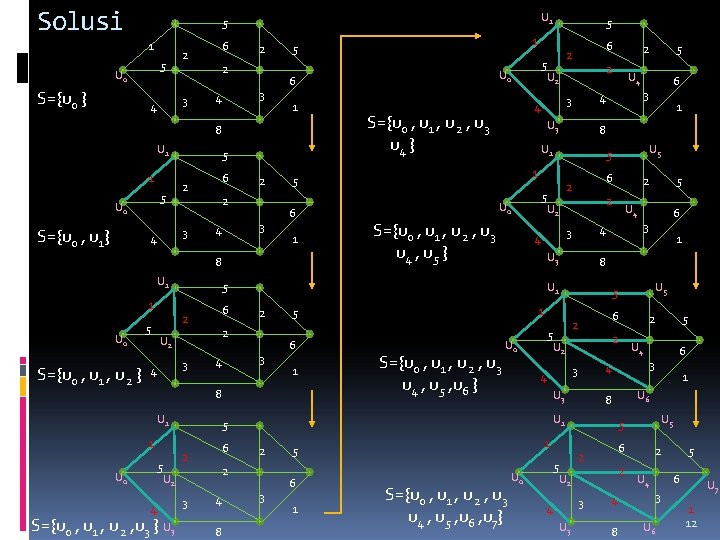
Solusi 1 5 U 0 S={u 0 } U 1 5 3 4 6 2 2 2 3 4 1 5 U 0 S={u 0 , u 1} 5 3 4 6 2 2 2 3 4 1 8 U 1 1 U 0 S={u 0 , u 1 , u 2 } 5 6 2 U 2 3 3 4 6 1 5 U 0 4 1 S={u 0 , u 1 , u 2 , u 3 u 4 , u 5 , u 6 } 5 6 2 U 2 3 4 8 2 U 2 3 1 6 1 S={u 0 , u 1 , u 2 , u 3 u 4 , u 5 , u 6 , u 7} 5 3 U 4 6 1 U 6 U 5 5 6 2 U 2 2 U 4 U 6 5 6 3 4 8 5 3 8 2 4 3 U 0 U 5 6 2 4 5 1 5 U 1 2 6 3 8 1 5 2 S={u 0 , u 1 , u 2 , u 3 } U 3 5 U 4 4 3 U 0 2 2 U 2 4 5 8 U 1 6 2 U 1 2 1 U 5 5 1 S={u 0 , u 1 , u 2 , u 3 u 4 , u 5 } 6 3 8 U 1 5 5 U 4 4 U 3 U 0 2 2 U 2 3 5 2 4 S={u 0 , u 1 , u 2 , u 3 u 4 } 6 2 4 5 6 5 U 0 6 8 U 1 1 5 U 7 1 12

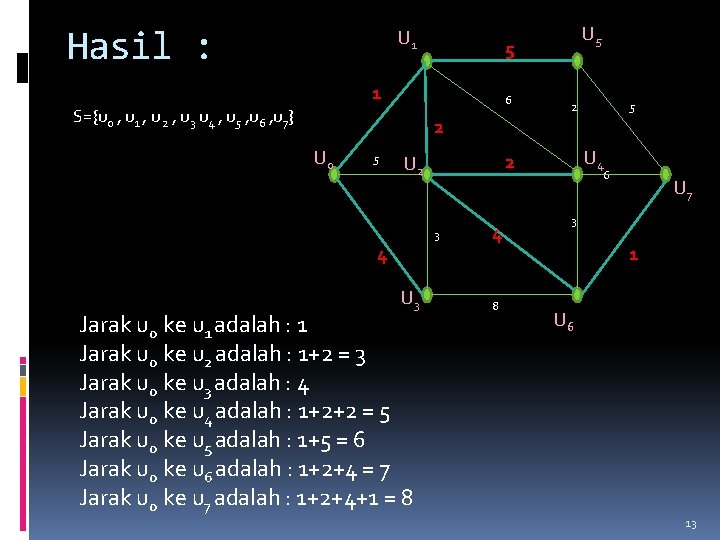
Hasil : U 1 1 6 S={u 0 , u 1 , u 2 , u 3 u 4 , u 5 , u 6 , u 7} 2 U 0 5 3 U 3 Jarak u 0 ke u 1 adalah : 1 Jarak u 0 ke u 2 adalah : 1+2 = 3 Jarak u 0 ke u 3 adalah : 4 Jarak u 0 ke u 4 adalah : 1+2+2 = 5 Jarak u 0 ke u 5 adalah : 1+5 = 6 Jarak u 0 ke u 6 adalah : 1+2+4 = 7 Jarak u 0 ke u 7 adalah : 1+2+4+1 = 8 2 4 8 5 U 4 2 U 2 4 U 5 5 6 U 7 3 1 U 6 13