Algorithms Minimum spanning tree Shortest path algorithms Prims

Algorithms Minimum spanning tree Shortest path algorithms

Prim’s Algorithm MST-Prim(G, w, r) Q = V[G]; for each u Q key[u] = ; key[r] = 0; p[r] = NULL; while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; p[r] = NULL; 3 8 while (Q not empty) Run on example graph u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; p[r] = NULL; 3 8 while (Q not empty) Run on example graph u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 r p[r] = NULL; 3 8 while (Q not empty) Pick a start vertex r u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 u p[r] = NULL; 3 8 while (Q not empty) u = Extract. Min(Q); Red vertices have been removed from Q for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 u p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); Red arrows indicate parent pointers for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 14 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 u p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 14 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 p[r] = NULL; 3 8 3 while (Q not empty) u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 14 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 2 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm MST-Prim(G, w, r) 6 4 Q = V[G]; 5 10 2 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15 15

Prim’s Algorithm u MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 10 2 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 15

Prim’s Algorithm u MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 10 2 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm u 4 MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 10 2 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm u 4 MST-Prim(G, w, r) 6 4 9 Q = V[G]; 5 5 2 for each u Q 14 key[u] = ; 2 10 15 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm u 4 MST-Prim(G, w, r) 6 4 Q = V[G]; 5 5 2 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm u 4 MST-Prim(G, w, r) 6 4 Q = V[G]; 5 5 2 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 15

Prim’s Algorithm 4 MST-Prim(G, w, r) 6 4 Q = V[G]; 5 5 2 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); u 9 15

Prim’s Algorithm 4 MST-Prim(G, w, r) 6 4 Q = V[G]; 5 5 2 for each u Q 14 key[u] = ; 2 10 key[r] = 0; 0 8 p[r] = NULL; 3 8 3 while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); 9 9 u 15 15

Review: Prim’s Algorithm MST-Prim(G, w, r) Q = V[G]; for each u Q key[u] = ; key[r] = 0; What is the hidden cost p[r] = NULL; while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v); in this code?

Review: Prim’s Algorithm MST-Prim(G, w, r) Q = V[G]; for each u Q key[u] = ; key[r] = 0; p[r] = NULL; while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; Decrease. Key(v, w(u, v));

Review: Prim’s Algorithm MST-Prim(G, w, r) Q = V[G]; What will be the running time? for each u Q key[u] = ; A: Depends on queue key[r] = 0; binary heap: O(E lg V) p[r] = NULL; Fibonacci heap: O(V lg V + E) while (Q not empty) u = Extract. Min(Q); for each v Adj[u] if (v Q and w(u, v) < key[v]) p[v] = u; key[v] = w(u, v);

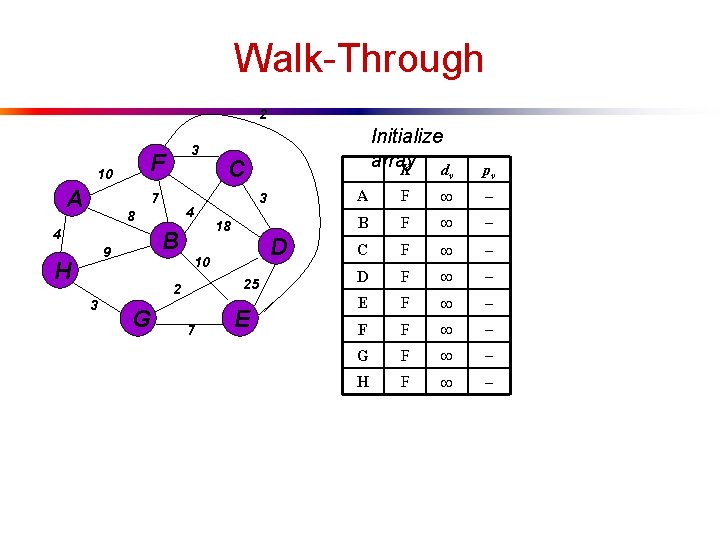
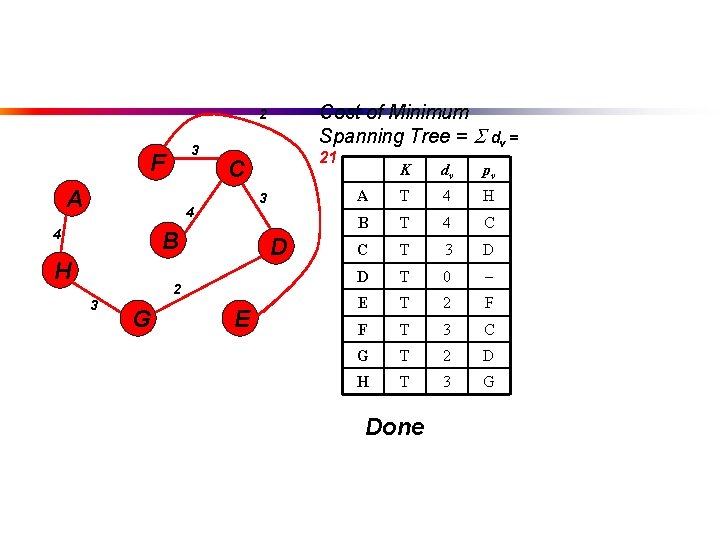
Walk-Through 2 F 10 A 3 7 4 8 4 B 9 H 3 18 D 10 25 2 3 C G 7 E Initialize array K d v pv A F B F C F D F E F F F G F H F

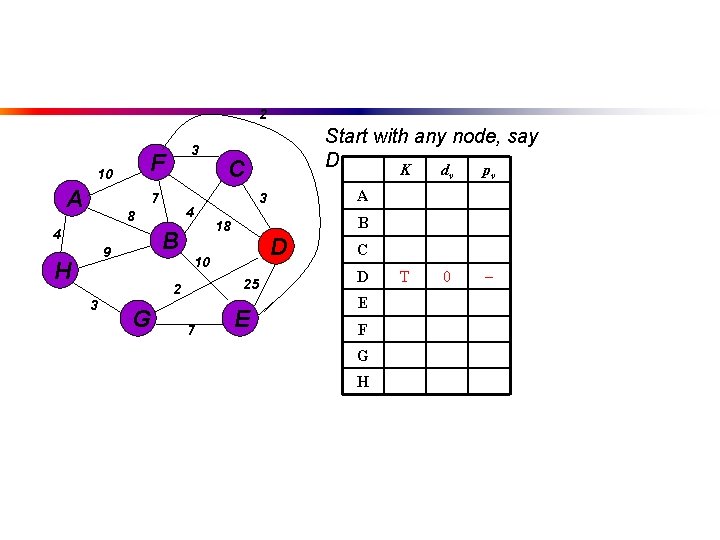
2 F 10 A 3 7 4 8 4 B 9 H 3 C G v 0 B 18 D 25 7 v A 3 10 2 Start with any node, say D K d p E C D E F G H T

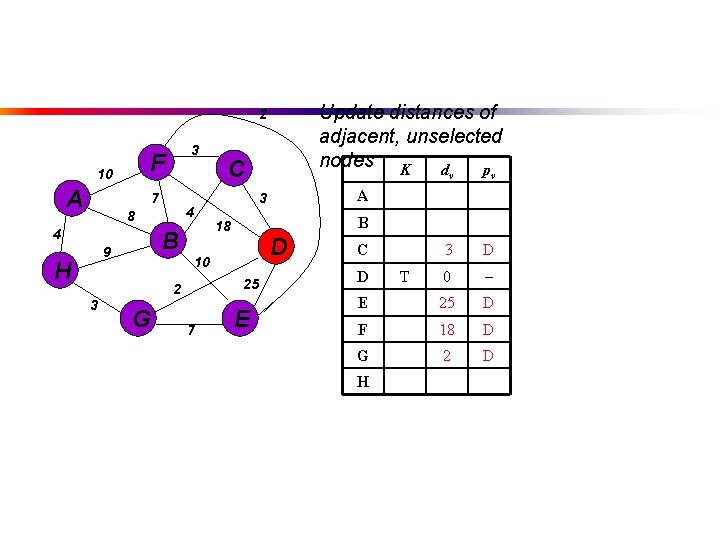
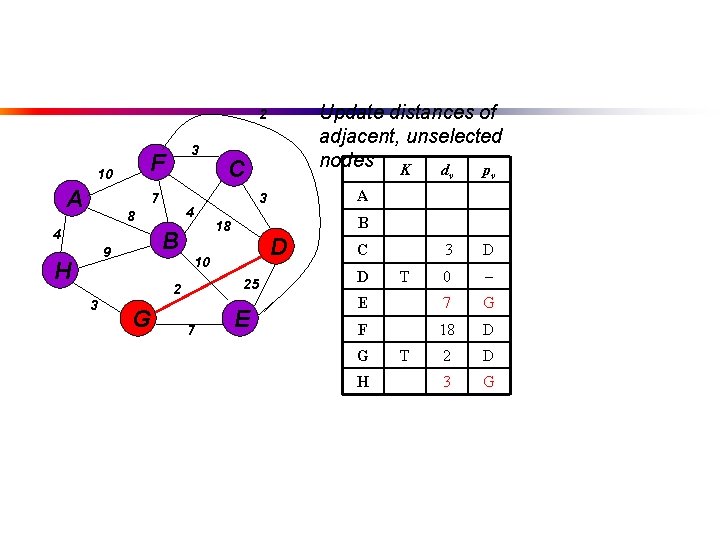
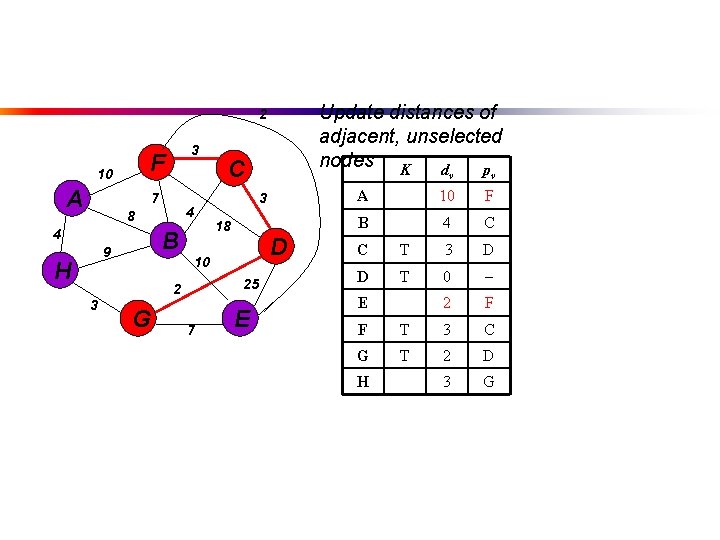
Update distances of adjacent, unselected nodes K d p 2 F 10 A 3 7 4 8 4 B 9 H G v 3 D 0 E 25 D F 18 D G 2 D B 18 D 25 7 v A 3 10 2 3 C E C D H T

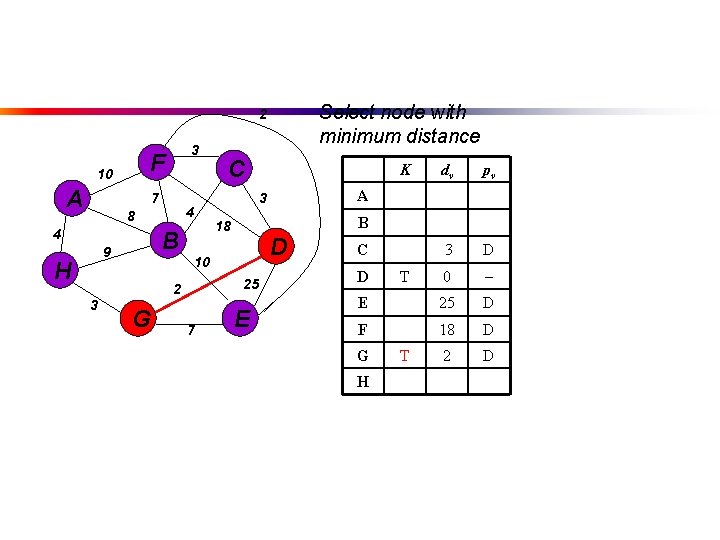
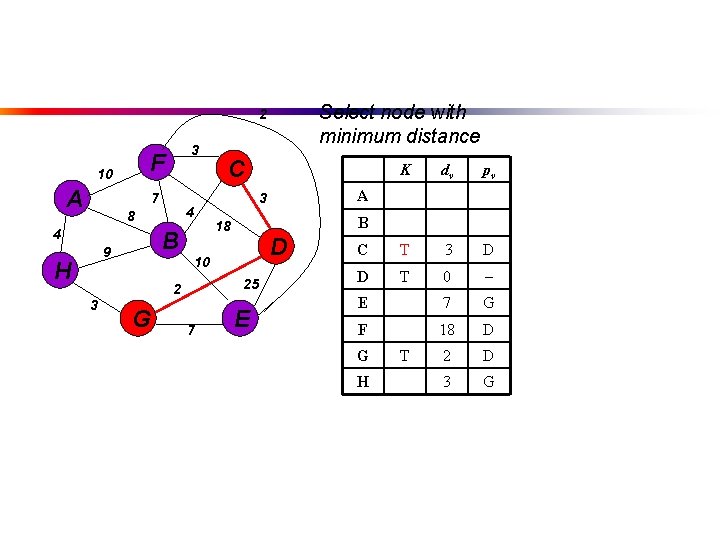
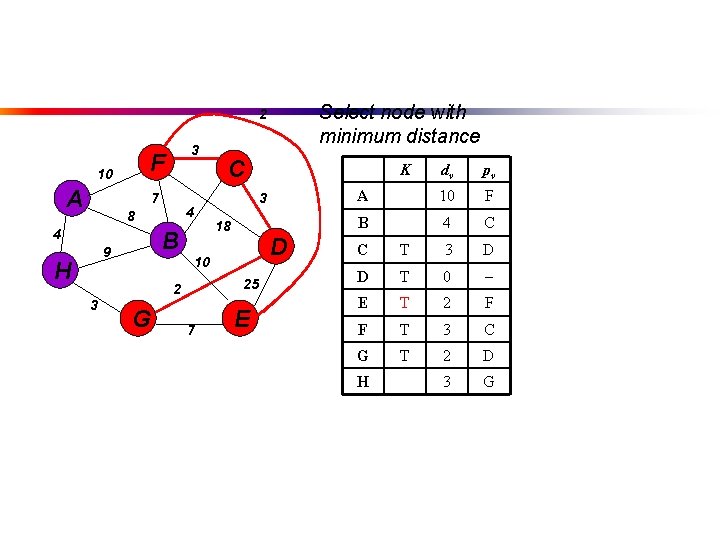
Select node with minimum distance 2 F 10 A 3 7 4 8 4 B 9 H G dv pv 3 D 0 E 25 D F 18 D 2 D A B 18 D 25 7 K 3 10 2 3 C E C D G H T T

Update distances of adjacent, unselected nodes K d p 2 F 10 A 3 7 4 8 4 B 9 H G v 3 D 0 E 7 G F 18 D 2 D 3 G B 18 D 25 7 v A 3 10 2 3 C E C D G H T T

Select node with minimum distance 2 F 10 A 3 7 4 8 4 B 9 H G dv pv C T 3 D D T 0 E 7 G F 18 D 2 D 3 G B 18 D 25 7 K A 3 10 2 3 C E G H T

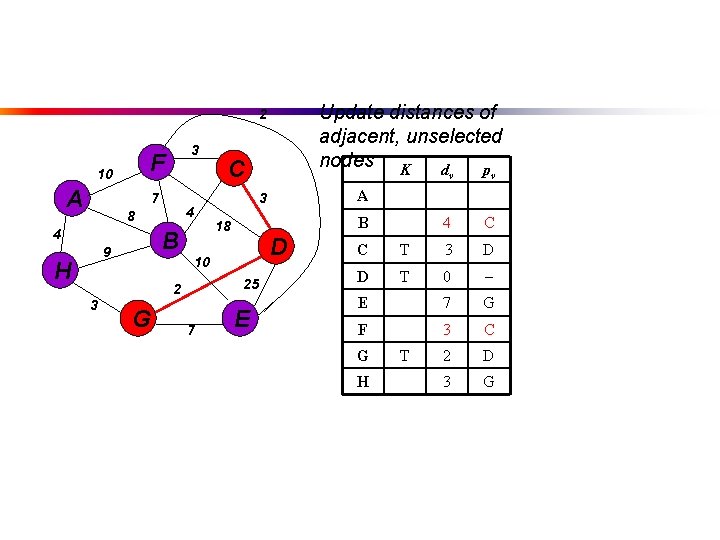
Update distances of adjacent, unselected nodes K d p 2 F 10 A 3 7 4 8 4 B 9 H B 18 D 25 G 7 E v v 4 C A 3 10 2 3 C C T 3 D D T 0 E 7 G F 3 C 2 D 3 G G H T

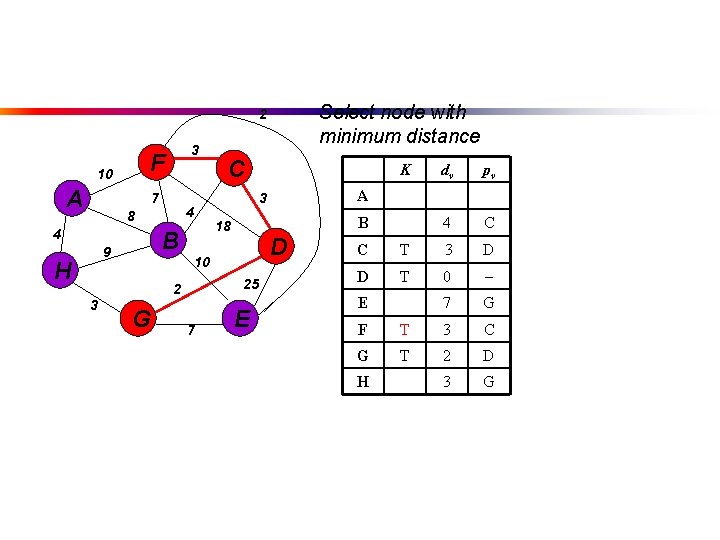
Select node with minimum distance 2 F 10 A 3 7 4 8 4 B 9 H G D E dv pv 4 C A B 18 25 7 K 3 10 2 3 C C T 3 D D T 0 7 G E F T 3 C G T 2 D 3 G H

Update distances of adjacent, unselected nodes K d p 2 F 10 A 3 7 4 8 4 B 9 H 3 18 D 10 25 2 3 C G 7 E v v A 10 F B 4 C C T 3 D D T 0 2 F E F T 3 C G T 2 D 3 G H

Select node with minimum distance 2 F 10 A 3 7 4 8 4 B 9 H G 18 D 25 7 K 3 10 2 3 C E dv pv A 10 F B 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D 3 G H

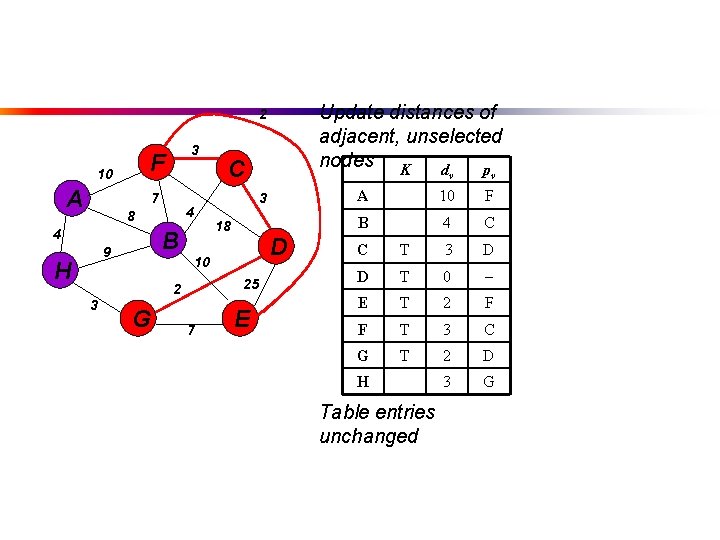
Update distances of adjacent, unselected nodes K d p 2 F 10 A 3 7 4 8 4 B 9 H 3 18 D 10 25 2 3 C G 7 E v v A 10 F B 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D 3 G H Table entries unchanged

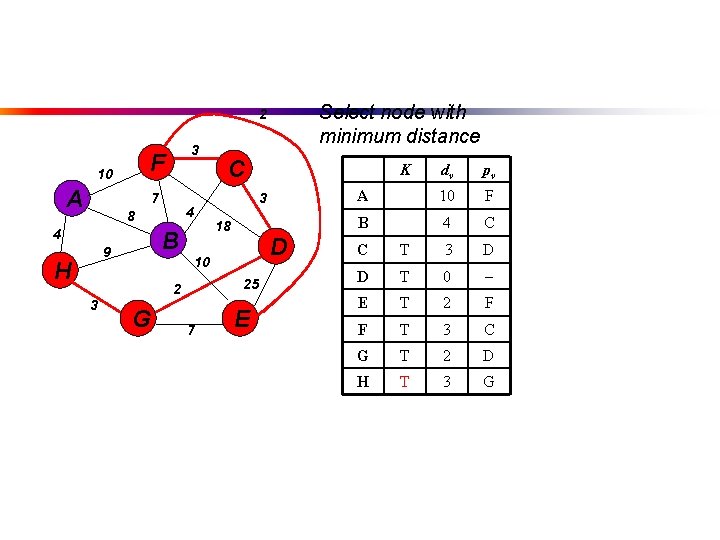
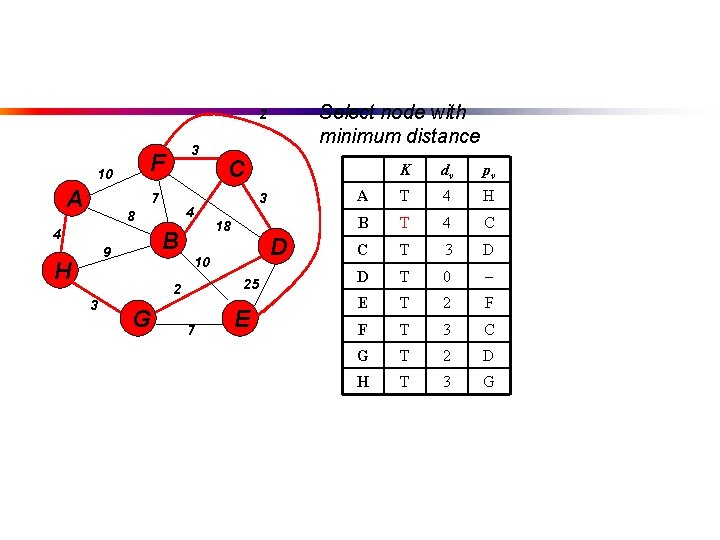
Select node with minimum distance 2 F 10 A 3 7 4 8 4 B 9 H G 18 D 25 7 K 3 10 2 3 C E dv pv A 10 F B 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G

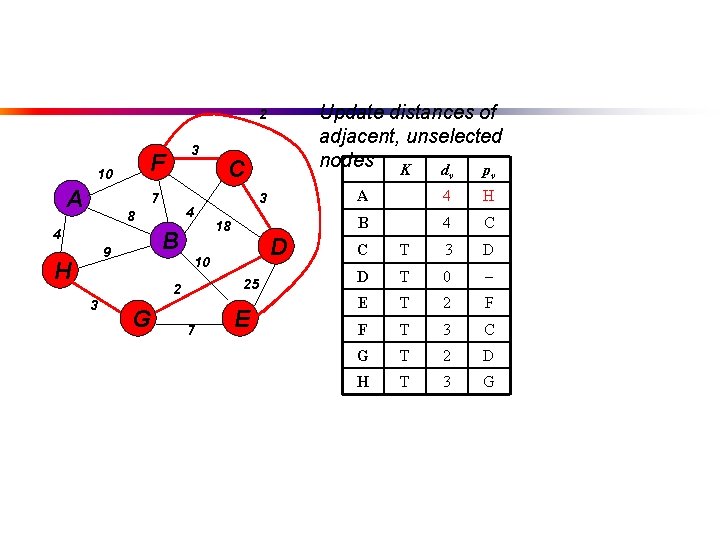
Update distances of adjacent, unselected nodes K d p 2 F 10 A 3 7 4 8 4 B 9 H 3 18 D 10 25 2 3 C G 7 E v v A 4 H B 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G

Select node with minimum distance 2 F 10 A 3 7 4 8 4 B 9 H G K dv pv T 4 H 4 C B 18 D 25 7 A 3 10 2 3 C E C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G

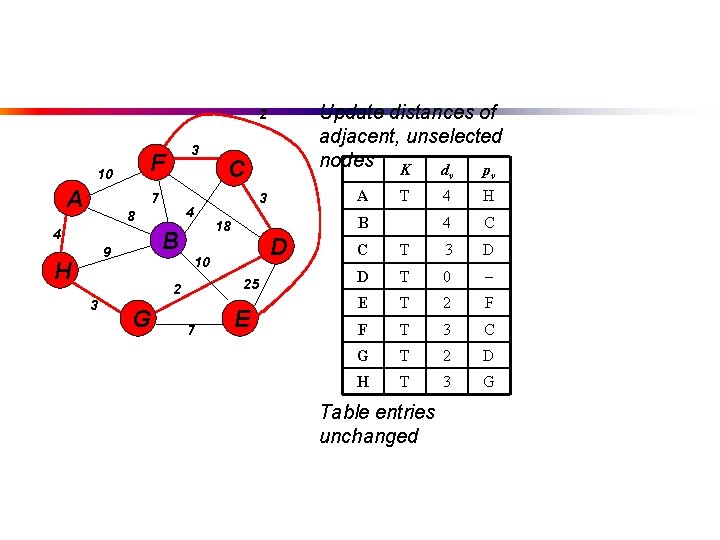
Update distances of adjacent, unselected nodes K d p 2 F 10 A 3 7 4 8 4 B 9 H G T B 18 D 25 7 A 3 10 2 3 C E v v 4 H 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G Table entries unchanged

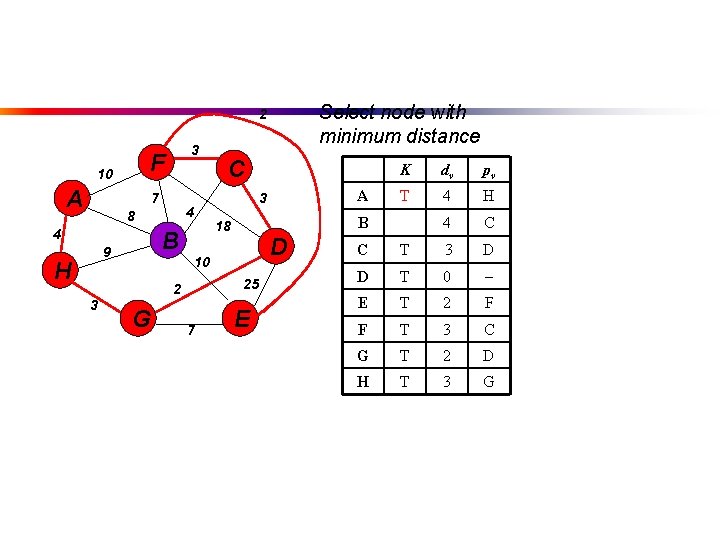
Select node with minimum distance 2 F 10 A 3 7 4 8 4 B 9 H 3 18 D 10 25 2 3 C G 7 E K dv pv A T 4 H B T 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G

Cost of Minimum Spanning Tree = dv = 2 3 F A C 3 4 4 B H D 2 3 G 21 E K dv pv A T 4 H B T 4 C C T 3 D D T 0 E T 2 F F T 3 C G T 2 D H T 3 G Done

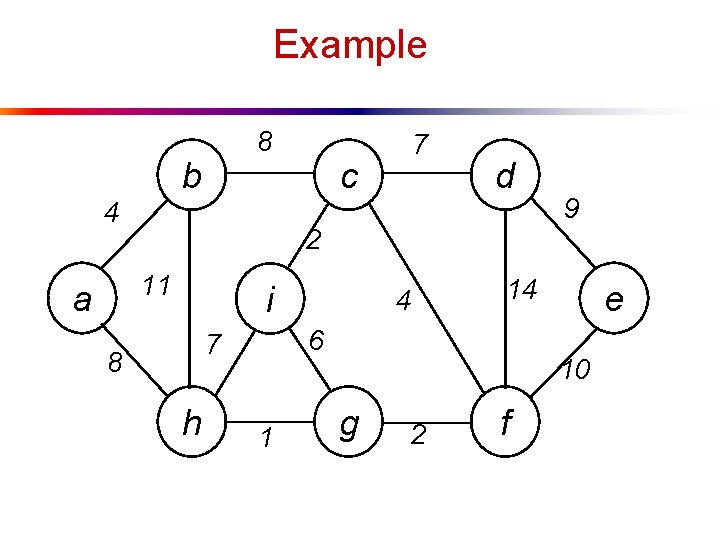
Example 8 b 4 c d 2 11 a 7 i h 14 6 7 8 4 1 9 e 10 g 2 f