ALGORITHMS LIST PROCESSING Lists v Sometimes a problem

ALGORITHMS LIST PROCESSING

Lists v Sometimes a problem deals with a list of values v We represent such a list with a single name, and use subscripts to indicate the individual members of the list v For example, if X is a list of size N, then the individual members are: X 1 , X 2 , X 3 , ………. , XN

Lists v Always include the size of the list as part of the information for the algorithm – remember storage? How much room must the computer set aside for our list? – there are techniques for working with lists of unknown length, but they are beyond the scope of this course. – either you will know the length of the list or you will be able to calculate it

Algorithm 4. 1 v Write an algorithm that returns the Kth element of a given list L, with N numbers – NAME: Find. K – GIVENS: L, N, K • Change: None – RESULTS: Val – INTERMEDIATES: None – DEFINITION: Val : = Find. K(L, N, K) – ------------– METHOD: Get L, N Get K Let Val = LK Give Val

Algorithm 4. 2 v Write an algorithm that replaces the Kth element`s value of a given list L (with N numbers) with the given value M – NAME: Change. K – GIVENS: L, N, K, M • Change: L – RESULTS: None – INTERMEDIATES: None – DEFINITION: Change. K(L, N, K, M) – ------------– METHOD: Get L, N Get K Get M Let LK = M Give L

Trace 4. 1 v Trace Algorithm 4. 2 with a list L of 5 elements (1, 8, 3, 6, 2) where K is 2 and M is 20 METHOD: (1) Get L, N (2) Get K (3) Get M (4) Let LK = M (5) Give L Ln L N K 1 (1, 8, 3, 6, 2) 5 2 2 3 4 (1, 20, 3, 6, 2) 5 output (1, 20, 3, 6, 2) M 20

Algorithm 4. 3 v Given a list, L, of N numbers, where N is odd, find the middle number in the list – NAME: Middle – GIVENS: L, N • Change: None – RESULTS: Mid – INTERMEDIATES: Loc – DEFINITION: Mid : = Middle(L, N) – ------------– METHOD: • Get L, N • Let Loc = N div 2 + 1 • Let Mid = Lloc • Give Mid

Trace 4. 2 v Trace Algorithm 4. 3 with a list L of 5 elements (1, 8, 3, 6, 2) METHOD: (1) Get L, N (2) Let Loc = N div 2 + 1 (3) Let Mid = Lloc (4) Give Mid LN 1 L (1, 8, 3, 6, 2) 2 3 4 output 3 N Loc Mid 5 3 3

List Processing v Remember that we represent a list with a single name and use subscripts ( )ﺩﻟﻴﻞ to indicate the individual members of the list v Processing a list usually involves a loop in which we use the list subscript variable as the loop control variable v Frequently, we also use Boolean operators in our loop tests – The next slide reviews use of these operators

List Processing v Assume that the Boolean variables X, Y and Z are set to the following values: X = True, Y = False, Z = True v The order of precedence for Boolean operators is Not, And, Or v What is the result of each of the following expressions: (X and Y) or Z = TRUE (True or Y) and False = FALSE X or True and not Y or Z = TRUE not(X and not Z or False and (True and Y)) = TRUE Y and Y or not Z = FALSE

Algorithm 4. 4 v Given a list X of N numbers, find the sum of the numbers in X v Analysis – Basic Algorithm • SUM • Let Total = 0 • Let Total = Total + ? ? – Total = X 1 + X 2 + ……. . + XN – Total = Total + XI • Let I go from 1 to N in a loop; then we will add each XI • Loop control variable is the list subscript variable

Algorithm 4. 4 v Given a list X of N numbers, find the sum of the numbers in X Method – Name: SUMLIST Get X, N – Given: X, N Let Total = 0 • Change: None Let I = 1 – Result: Total Loop When (I <= N) – Intermediate: I Let Total = Total + XI – Definition Let I = I + 1 • Total : = SUMLIST(X, N) Finish Loop Give Total

Trace 4. 3 v Trace algorithm 4. 4 with the list (3, 7, 5). N is 3. (1) Get X, N (2) Let Total = 0 (3) Let I = 1 (4) Loop When (I <= N) (5) Let Total = Total + XI (6) Let I = I + 1 (7) Finish Loop (8) Give Total LN X N I 1 (3, 7, 5) 3 2 3 1 4 5 6 Total Test 0 (1 <= 3) 3 2 4 5 6 (2 <= 3) 10 3 4 5 6 4 (3 <= 3) 15 4 (4 <= 3) 8 Output 15

Algorithm 4. 5 v Given a list X of N numbers, determine whether the given value V occurs in the list X. v Analysis – Basic Algorithm • SEARCH • Let Found = False • Does XI = V? – Stop the index at this point » FOUND at XI – I to process the list

Algorithm 4. 5 v Given a list X of N numbers, determine whether the given value V occurs in the list X. Name: SEARCHX Method Get X, N Given: X, N, V Get V Change: None Let Found = False Let I = 1 Result: Found Loop Intermediate: I If (XI = V) Let Found = True Definition: Else Found : = SEARCHX(X, N, V) Let I = I + 1 Finish Loop When (I >N) or (Found) Give Found

Trace 4. 4 v Trace algorithm 4. 5 with the list (3, 7, 5) and with a value of 7 for V (1) (2) (3) (4) (5) (6) (7) (8) (9) Get X, N Get V Let Found = False Let I = 1 Loop If (XI = V) Let Found = True Else Let I = I + 1 LN X N V 1 (3, 7, 5) 3 2 7 3 4 6 9 10 6 7 10 (10) Finish Loop When (I >N) or Found 11 Output True (11) Give Found I Found Test False 1 (3 = 7) 2 (2>3) or (F) (7 = 7) True (2>3) or (T)

Algorithm 4. 6 v Given a list X of N positive numbers, find the maximum number and its position in X v Analysis – Basic Algorithm • MAX • Let Max = -1 • (XI > Max)? – I for list processing • Must track not only the Max, but also the location of Max (the value of I)

Algorithm 4. 6 v Given a list X of N positive numbers, find the maximum number and its position in X – Name: MAXLIST – Given: X, N • Change: None – Result: Max, Loc – Intermediate: I – Definition: – (Loc, Max) : = MAXLIST(X, N) Method Get X, N Let Max = -1 Let I = 1 Loop When (I <= N) If (XI > Max) Let Max = XI Let Loc = I Let I = I + 1 Finish Loop Give Max Give Loc

Trace 4. 5 v Trace algorithm 4. 6 with the list (8, 3, 25, 9) (1) Get X, N (2) Let Max = -1 (3) Let I = 1 (4) Loop When (I <= N) (5) If (XI > Max) (6) Let Max = XI (7) Let Loc = I (8) (9) Let I = I + 1 Finish Loop (10) Give Max (11) Give Loc LN X N 1, 2, 3 (8, 3, 25, 9) 4 4 5 6 7 8 4 5 8 4 10 Output 25 11 Output 3 I 1 MAX -1 LOC TEST (1 <= 4) (8 > -1) 8 1 2 (2 <= 4) (3 > 8) 3 (3 <= 4) (25>8) 25 3 4 (4 <= 4) (9>25) 5 (5 <= 4)

Algorithm 4. 7 v Given a list X of N numbers, find the number of times zero occurs in the list v Analysis – Basic Algorithm • • COUNT Let Count = 0 XI = 0? Let Count = Count + 1 if a match – I for list processing

Algorithm 4. 7 v Given a list X of N numbers, find the number of times zero occurs in the list – Name: NUM 0 – Given: X, N • Change: None – Result: Count – Intermediate: I – Definition: – Count : = NUM 0(X, N) Method Get X, N Let Count = 0 Let I = 1 Loop When (I <= N) If (XI = 0) Let Count = Count + 1 Let I = I + 1 Finish Loop When Give Count

Algorithm 4. 8 v Given a list X of N numbers, see if X contains any two numbers which are the same v Analysis – Basic Algorithm • Variant of SEARCH • Compare each XI with every other element of the list • Loop within a Loop – For each XI » Search for XI • Search only until one match is found – Stop the Indexes at the locations

Algorithm 4. 8 v Given a list X of N numbers, see if X contains any two numbers which are the same Method Get X, N Let Double = False Let Test = 1 Loop Let I = Test + 1 Loop If (XTest = XI) Let Double = True Else Let I = I + 1 Finish Loop When (I >N) or (Double) If (Not (Double)) Let Test = Test + 1 Finish Loop When (Test = N) or (Double) – Name: DUPLICATE – Given: X, N • Change: None – Result: Double – Intermediate: I, Test – Definition: – Double : = DUPLICATE(X, N) Give Double

Trace 4. 6 v (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) Trace algorithm 4. 8 with the list (2, 8, 7, 8) Get X, N Let Double = False Let Test = 1 Loop Let I = Test +1 Loop If (XTest = XI) Let Double = True Else Let I = I + 1 Finish Loop When (I >N) or (Double) If (Not(Double)) Let Test = Test + 1 Finish Loop When (Test = N) or (Double) (15) Give Double LN X N Double Test I TEST 1, 2, 3 (2, 8, 7, 8) 4 False 1 5 2 7 (2=8) 10 3 11 (3>4)or(F) 7 (2=7) 10 4 11 (4>4)or(F) 7 (2=8) 10 5 11 (5>4)or(F) 12 Not (F) 13 2 14 (2=4)or(F) 5 3 7 (8=7) 10 4 11 (4>4)or(F) 7 (8=8) 8 True 11 (5>4)or(T) 12 Not (T) 14 (3=4)or(T) 15 Output True

Grouped Lists v If we want to process multiple, related lists (as in a database), we must maintain the order relationship between elements in each list v E. g. Student grades – – – Name - Midterm - Final Ann - 100 - 30 Bob - 75 - 28 Cathy - 60 - 90 Dave - 40 - 80

Grouped Lists v We have three lists – Name = (Ann, Bob, Cathy, Dave) – Midterm = (100, 75, 60, 40) – Final = (30, 28, 90, 80) v Since Ann is Name 1, then her midterm mark would be Midterm 1 and her final mark would be Final 1 v We can also create a new list from other lists.

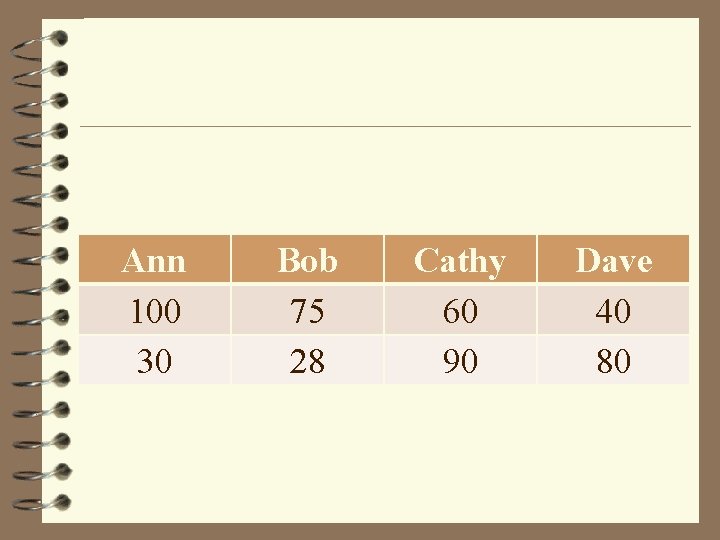
Ann 100 30 Bob 75 28 Cathy 60 90 Dave 40 80

Algorithm 4. 9 v Given two lists, Midterm and Final, of N numbers each, calculate a Final grade of 75% Final and 25% Midterm – Name: FINDGRADE – Given: M, F, N • Change: None Method Get M, F, N Let I = 1 – Result: G – Intermediate: I – Definition: – G : = FINDGRADE(M, F, N) Loop When (I <= N) Let GI = 0. 75*FI + 0. 25*MI Let I = I + 1 Finish Loop Give G

Trace 4. 7 v Trace algorithm 4. 9 with the grouped list defined previously F = (30, 28, 90, 80) M = (100, 75, 60, 40) LN 1, 2 3 4 5 I N G Test 1 4 (? ? , ? ? ) (1 <= 4) (48, ? ? ) 2 Method (1) Get M, F, N (2) Let I = 1 (3) (4) (5) (6) Loop When (I <= N) Let GI = 0. 75*FI + 0. 25*MI Let I = I + 1 Finish Loop (7) Give G 3 4 5 3 (2 <= 4) (48, 40, ? ? ) 3 (3 <= 4) (48, 40, 83, ? ? ) 4 (4 <= 4) (48, 40, 83, 70) 5 7 Output (48, 40, 83, 70) (5 <= 4)

Algorithm 4. 10 v Given a set of lists, Name and Grade, determine who received the lowest grade. Method Get Name, G, N – Name: WORST Let Min = 101 – Given: Name, G, N Let I = 1 • Change: None Loop When (I <= N) – Result: LName If (GI < Min) – Intermediate: Let Min = GI • Loc, Min, I Let Loc = I – Definition: – Lname : =WORST(Name, G, N) Let I = I + 1 Finish Loop Let LName = Name. Loc Give LName

Name = (Ann, Bob, Cathy, Dave) G = (48, 40, 83, 70) Trace 4. 8 v (1) (2) (3) (4) (5) (6) (7) LN 1, 2, 3 4 5 6 Trace algorithm 4. 10 with the 7 grouped list defined previously 8 Get Name, G, N Let Min = 101 Let I = 1 Loop When (I <= N) If (GI < Min) Let Min = GI Let Loc = I (8) Let I = I + 1 (9) Finish Loop (10) Let LName = Name. Loc (11) Give LName 4 5 6 7 8 4 5 8 4 10 11 N 4 I 1 LOC MIN Lname 101 TEST (1 <= 4) (48<101) 48 1 2 (2<=4) (40<48) 40 2 3 (3<=4) (83<40) 4 (4<=4) (70<40) 5 (5<=4) Bob Output Bob

Additional Material

Flow Charts

Algorithm 4. 1 v Write an algorithm that returns the Kth element of a given list L, with N numbers NAME: Find. K GIVENS: L, N, K Change: None RESULTS: Val INTERMEDIATES: None DEFINITION: Val : = Find. K(L, N, K)

Algorithm 4. 2 Write an algorithm that replaces the Kth element`s value of a given list L (with N numbers) with the given value M NAME: Change. K GIVENS: L, N, K, M Change: L RESULTS: None INTERMEDIATES: None DEFINITION: Change. K(L, N, K, M)

Algorithm 4. 3 Given a list, L, of N numbers, where N is odd, find the middle number in the list NAME: Middle GIVENS: L, N Change: None RESULTS: Mid INTERMEDIATES: Loc DEFINITION: Mid : = Middle(L, N)

Algorithm 4. 4 Given a list X of N numbers, find the sum of the numbers in X Name: SUMLIST Given: X, N Change: None Result: Total Intermediate: I Definition Total : = SUMLIST(X, N)

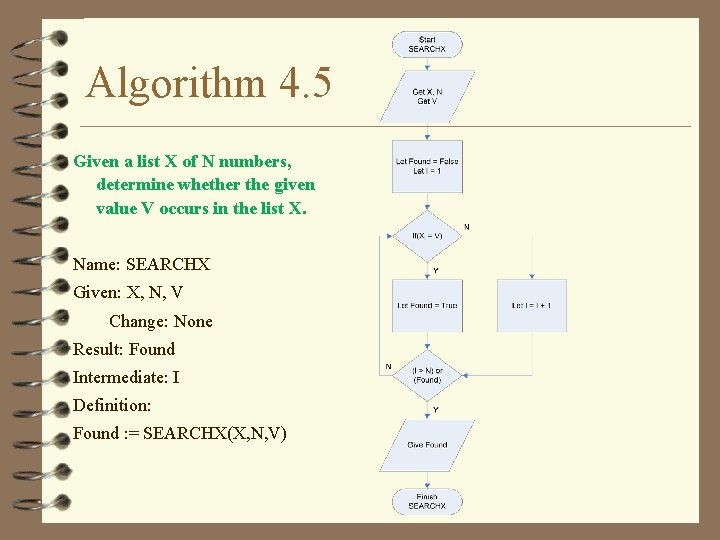
Algorithm 4. 5 Given a list X of N numbers, determine whether the given value V occurs in the list X. Name: SEARCHX Given: X, N, V Change: None Result: Found Intermediate: I Definition: Found : = SEARCHX(X, N, V)

Algorithm 4. 6 Given a list X of N positive numbers, find the maximum number and its position in X Name: MAXLIST Given: X, N Change: None Result: Max, Loc Intermediate: I Definition: (Loc, Max) : = MAXLIST(X, N)

Algorithm 4. 7 Given a list X of N numbers, find the number of times zero occurs in the list Name: NUM 0 Given: X, N Change: None Result: Count Intermediate: I Definition: Count : = NUM 0(X, N)

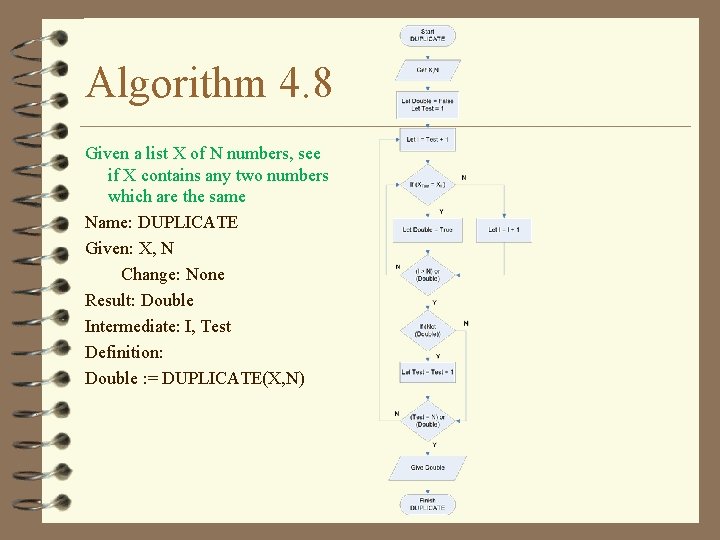
Algorithm 4. 8 Given a list X of N numbers, see if X contains any two numbers which are the same Name: DUPLICATE Given: X, N Change: None Result: Double Intermediate: I, Test Definition: Double : = DUPLICATE(X, N)

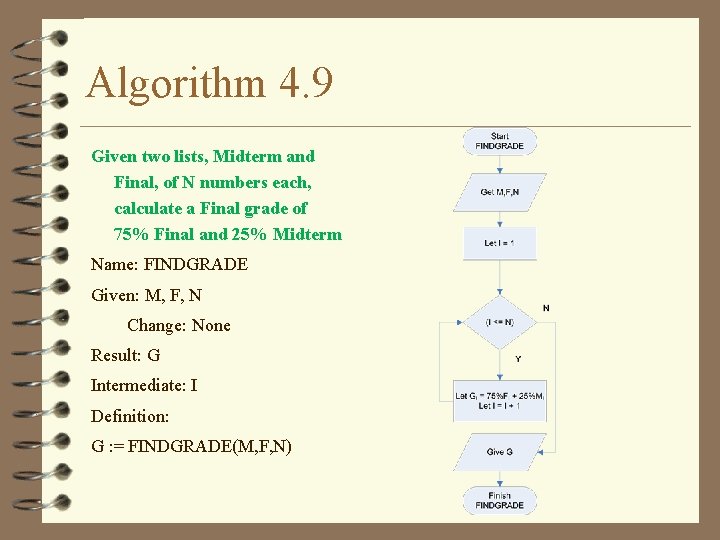
Algorithm 4. 9 Given two lists, Midterm and Final, of N numbers each, calculate a Final grade of 75% Final and 25% Midterm Name: FINDGRADE Given: M, F, N Change: None Result: G Intermediate: I Definition: G : = FINDGRADE(M, F, N)

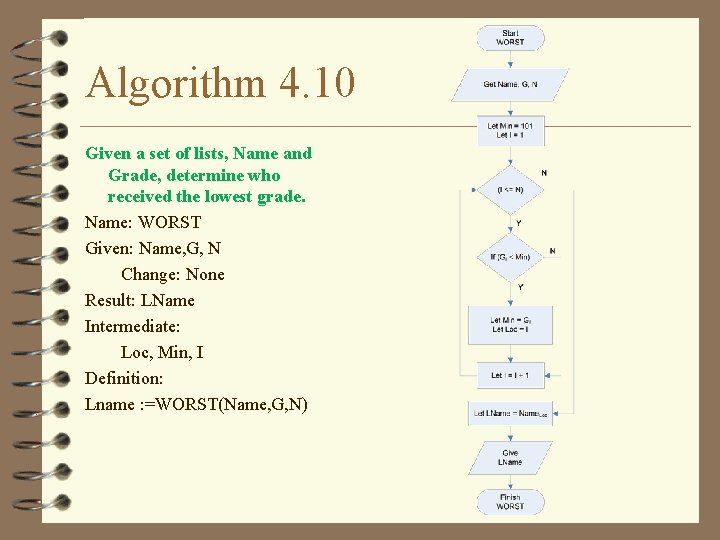
Algorithm 4. 10 Given a set of lists, Name and Grade, determine who received the lowest grade. Name: WORST Given: Name, G, N Change: None Result: LName Intermediate: Loc, Min, I Definition: Lname : =WORST(Name, G, N)

Homework

Write an algorithm to find the maximum value in a list of positive numbers. Each entry in the list is unique (ie. There are no duplicate numbers) Write an algorithm that fills a list with the first 50 multiples of 7. (ie. 7, 14, 21… 350) Write an algorithm to populate a list with names. The list will continue to grow until the user indicates it is time to stop.