Algorithms Lecture 8 Divideandconquer algorithms Divideandconquer paradigm Key

Algorithms Lecture 8

Divide-and-conquer algorithms

Divide-and-conquer paradigm • Key idea: break problem into smaller versions of the same problem (“sub-problems”) – Should be “easy” to use solutions to sub-problems to construct a solution to the original problem

General framework • Solve(P) – If P is small enough, • Compute answer A directly, return A – Else • Construct sub-problems P 1, …, Pk • For i = 1, …, k: – Ai = Solve(Pi) • A = Combine(A 1, …, Ak), return A • Complexity of Solve determined by: – Number of sub-problems k and their size (as a function of the size of the original problem P) – Complexity of the Combine operation

Merge. Sort • Merge. Sort(P) – If |P| = 2, then sort P and return the result – Else • Let P 1, P 2 be the two halves of P • A 1 = Merge. Sort(P 1), A 2 = Merge. Sort(P 2) • A = Merge(A 1, A 2) // O(|P|) time • How to analyze the running time?

Merge. Sort running time • Let T(n) = running time of Merge. Sort on input of length n • We have T(n) ≤ 2 T(n/2) + c n, T(1), T(2) ≤ c for some constant c • How to solve for T(n)?

Approach 1: Unroll the recurrence • Imagine a binary tree corresponding to the recursive calls made on an input of length n – O(log n) levels • For each node, look at the work done in that function call itself (i. e. , not including the work done in any recursive calls) – So T(n) = the sum of the work done by all the nodes • We have – Root node (node at level 0) does c n work – Nodes at level 1 do 2 (c n/2) = cn work – Nodes at level i do 2 i (c n/2 i) = cn work Total work O(n log n)

Approach 2: Guess-and-check • Guess that T(n) ≤ cn log n for n ≥ 2 • Check: – T(1), T(2) ≤ c ≤ 2 c – Assume true for n < N; want to prove it true for N – T(N) ≤ 2 T(N/2) + c N ≤ c. N (log N – 1) + c N = c. N log N • Warning: easy to get a (correct but) loose upper bound this way

Approach 3: General recurrences • Many common recurrence relations have already been worked out • E. g. , T(n) ≤ a. T(n/2) + c n, a > 2 has the solution T(n) = O(nlog a) • E. g. , T(n) ≤ 2 T(n/2) + c n 2 has the solution T(n) = O(n 2) • Master theorem gives a general result

(Simplified) Master theorem • Let a ≥ 1, b > 1, k be constants, and say T(n) = a T(n/b) + c nk. Then: – If a > bk then T(n) = (nlogb a) – If a = bk then T(n) = (nk log n) – If a < bk then T(n) = (nk)

Divide-and-conquer algorithms • Closest pair of points – Cleverness in combining recursive solutions • Computational arithmetic (exponentiation, integer multiplication, matrix multiplication) – Important for cryptography – Cleverness in generating recursive sub-problems (and, in some cases, combining the solutions) • Fast Fourier Transform (FFT) – Very clever algorithm – Applications in ML, cryptography, computer vision, engineering, signal processing, etc.

Closest pair of points

Closest pair of points • Consider a set of n points in a plane (2 -D) – Assume for simplicity that none have the same xor y-coordinate – Consider the Euclidean distance between points • Goal: find the closest pair of points • Naïve algorithm: compute distance between every pair of points (O(n 2)-time algorithm) – Is it possible to do better?

Consider the 1 -D case • We can sort the points and then check distances between adjacent points – O(n log n) time • This does not translate to the 2 -D case – Points in 2 -D do not have a natural order

Divide-and-conquer approach I • Divide points P into two halves Q, R • Recursively find closest points (q, q’) in Q and (r, r’) in R, with distances Q, R, respectively • Key observation #1: – The closest points in P are either (q, q’) or (r, r’) or (q*, r*) for some q* Q and r* R – If we compute the distance between all points in Q and all points in R we get an O(n 2) algorithm!

Divide-and-conquer approach II • As before, but now Q and R are on the left and right sides of a vertical boundary line L • Let Q, R be as before, and =min{ Q, R} • Are there points q* Q, r* R closer than ? • Key observation #2: – We only need to consider points in Q, R within distance of L! – Unfortunately, it could happen that all points are within of L

Divide-and-conquer approach III • Q, R, L, as before; let S be the points (whether in Q or R) within distance of L – Are there points s, s’ S closer than ? • Say points in S are sorted by y-coordinate • Key observation #3: – Don’t need to compare each point in S with every other point in S! – Suffices to compare each s S with the next 15 points in S(!)

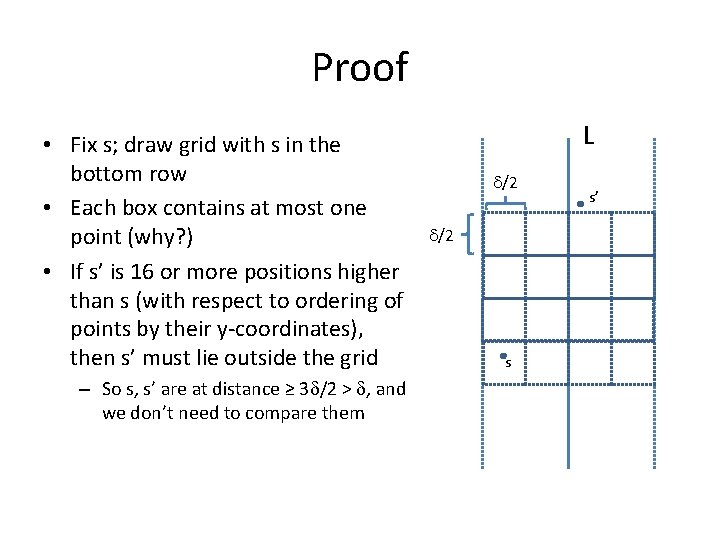
Proof • Fix s; draw grid with s in the bottom row • Each box contains at most one point (why? ) • If s’ is 16 or more positions higher than s (with respect to ordering of points by their y-coordinates), then s’ must lie outside the grid – So s, s’ are at distance ≥ 3 /2 > , and we don’t need to compare them L /2 /2 s s’

Divide-and-conquer overview • Divide points P into two halves Q, R by line L • Find closest points (q, q’) in Q and (r, r’) in R, with distances Q, R; let =min{ Q, R} • Let S = {s 1, …, sk} P be points within of L, sorted by their y-coordinates (note k ≤ n) • For i=1, …, k: for j = i+1, …, i+15: check if d(si, sj) < • T(n) = 2 T(n/2) + cn T(n) = O(n log n)

Details • Need to implement everything (besides the recursive calls) in O(n) time • Ideas: – Sort P by x- and y-coordinates (respectively) to get sorted lists Px and Py • Also keep track of each point’s location in each list – Only do this once (at the beginning)! • O(n log n) time – Recursively define Closest-Pair-Rec(Px, Py)

Details • Closest-Pair-Rec(Px, Py) works as follows: – Define Q = left half of Px; R = right half of Px Let L be the line through the rightmost point of Q – Easy to generate Qx, Rx; use Py to construct Qy, Ry (can all be done in one linear scan of Px, Py) – Call Closest-Pair-Rec on (Qx, Qy) and (Rx, Ry) to get two pairs of points, and compute – Define S (and Sx, Sy) using one linear scan of Px – Compare elements in S as before to get the closest pair of points in P