ALGORITHMS Introduction CS 8833 Algorithms Definition Algorithm Any

ALGORITHMS Introduction CS 8833 Algorithms

Definition Algorithm: Any well-defined computational procedure that takes some value or set of values as input and produces some value or set of values as output. CS 8833 Algorithms

Properties of Algorithms l Input – an algorithm has input values from a specified set l Output – for each set of input values, an algorithm produces output values from a specified set l Definiteness – the steps of the algorithm must be defined precisely CS 8833 Algorithms

Properties of Algorithms (cont) l Finiteness – an algorithm should produce the desired output after a finite number of steps for any input in the set l Effectiveness – it must be possible to perform each step of an algorithm exactly in a finite amount of time l Generality – the algorithm should be applicable for all problems of the desired form, not just a set of input values CS 8833 Algorithms

Question 1 l How do you show that an algorithm is incorrect? CS 8833 Algorithms

Question 2 l How do you show that an algorithm is correct ? CS 8833 Algorithms

Computational Model for Analysis l One processor random-access machine (RAM) – instructions are executed one at a time – no concurrent operations CS 8833 Algorithms

Choosing the “Best” Algorithm l Empirical approach – try competing algorithms on several different problem instances l Theoretical approach – determine mathematically the quantity of resources (execution time and memory) needed by the algorithm as a function of the size of the instance considered CS 8833 Algorithms

What is “Input Size”? Problem dependent l Identification of objects in problem processed by algorithm l – Number of items in the input is often used (e. g. length of an array) – Sometimes use number of bits – May use more than one measure (number of edges and vertices in a graph) CS 8833 Algorithms

What is the “Running Time” Number of primitive operations or “steps” executed. l Want this definition to be machine independent l Initial view taken by text – constant amount of time for each line of pseudocode l CS 8833 Algorithms

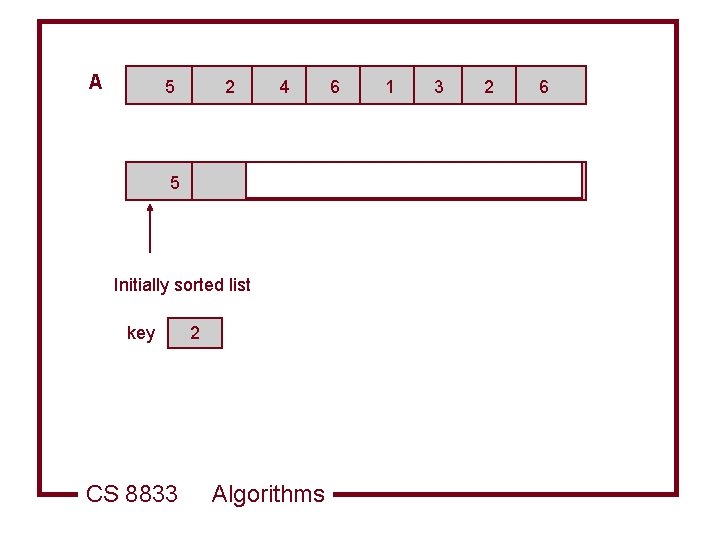
Insertion Sort Example Commonly used sorting algorithm l Sorting of playing cards often used as an analogy l CS 8833 Algorithms

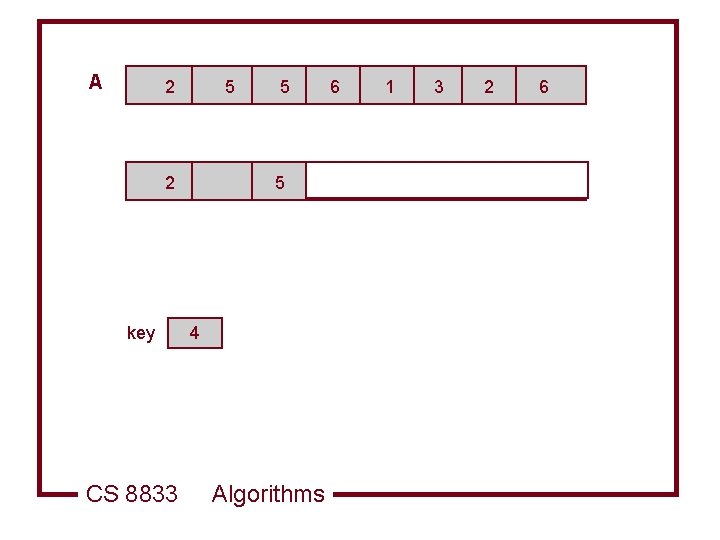
A 5 2 5 4 6 1 3 2 6 Initially sorted list key CS 8833 2 Algorithms

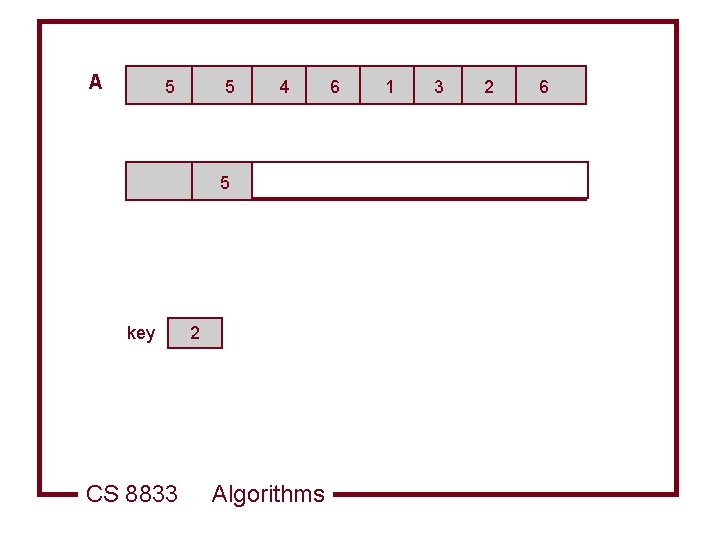
A 5 key CS 8833 5 4 6 1 3 2 6 2 Algorithms

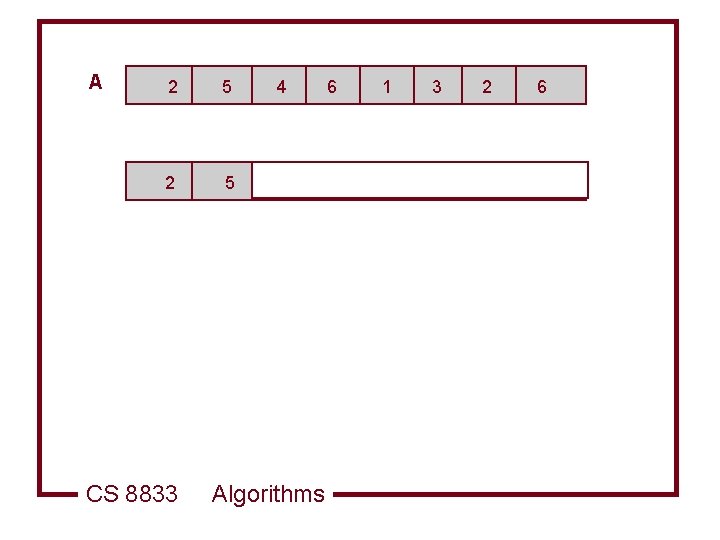
A 2 5 4 6 1 3 2 6 CS 8833 Algorithms

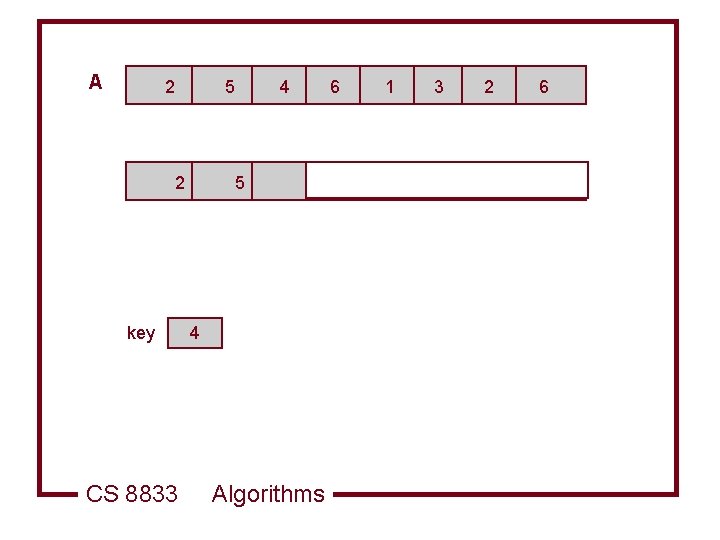
A 2 5 2 key CS 8833 5 4 6 6 4 Algorithms 1 1 3 3 2 2 6 6

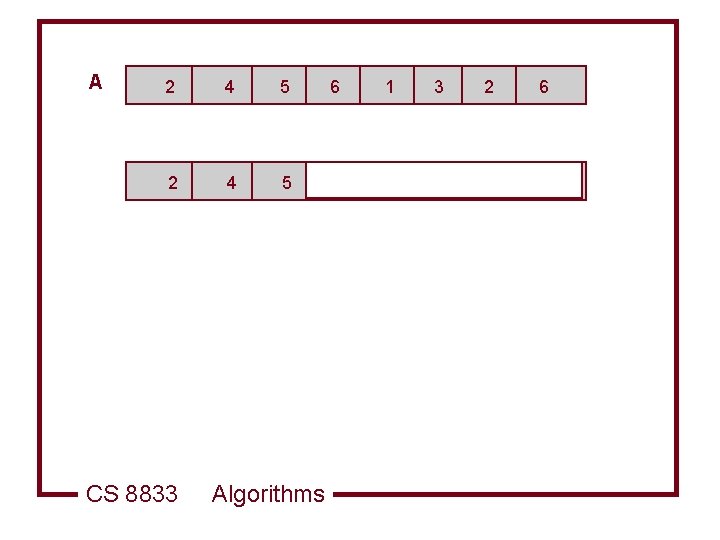
A 2 5 2 key CS 8833 5 6 1 3 2 6 4 Algorithms

A 2 4 5 6 1 3 2 6 CS 8833 Algorithms

INSERTION-SORT (A) cost time c 1 n c 2 n-1 ; sequence A[1. . j -1] 0 n-1 4 i j - 1 c 4 n-1 5 while i > 0 and A[i] > key do c 5 1 for j 2 to length[A] do 2 key A[j] 3 ; Insert A[j] into the sorted 6 A[i+1] A[i] c 6 7 i i- 1 c 7 A[i+1] key 8 CS 8833 Algorithms c 8 n-1

Running Time for Insertion Sort CS 8833 Algorithms

Why Worst Case Analysis? Gives an upper bound on the running time for any input l For some algorithms, the worst case occurs fairly often l Difficult to identify the average case l Difficult to analyze the average case l The average case is often roughly as bad as the worst case. l CS 8833 Algorithms

Order of Growth Consider only the highest order terms in formulas l Ignore the leading term’s constant coefficient l For insertion sort the worst case running time is (n 2) l CS 8833 Algorithms

Designing Algorithms A number of design paradigms for algorithms that have proven useful for many types of problems l Insertion sort – incremental approach l Other examples of design approaches l – divide and conquer – greedy – dynamic programming CS 8833 Algorithms

Divide and Conquer Good divide and conquer algorithm generally implies easy recursive version of the algorithm l Three steps l – divide – conquer – combine CS 8833 Algorithms

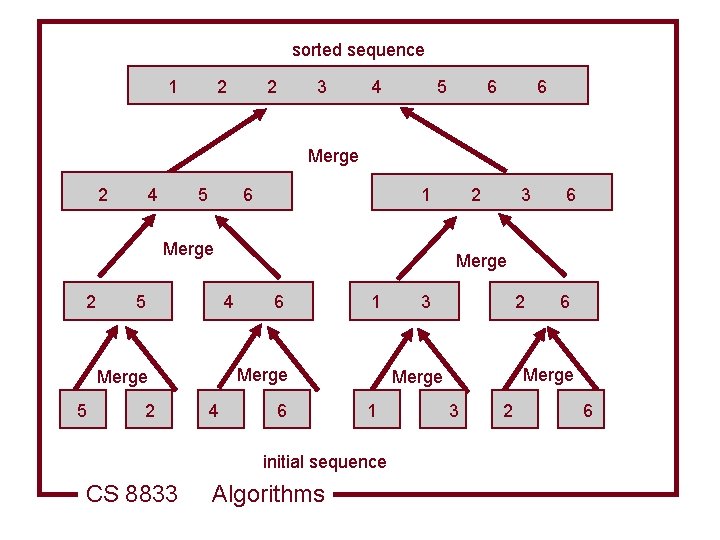
Merge Sort l Divide divide and n-element sequence into two n/2 element sequences l Conquer if the resulting list is of length 1 it is sorted else call the merge sort recursively l Combine merge the two sorted sequences CS 8833 Algorithms

MERGE-SORT (A, p, r) 1 if p < r then q (p+r)/2 2 3 MERGE-SORT(A, p, q) 4 MERGE-SORT(A, q+1, r) 5 MERGE(A, p, q, r) To sort A[1. . n], invoke MERGE-SORT with MERGE-SORT(A, 1, length(A)) CS 8833 Algorithms

sorted sequence 1 2 2 3 4 5 6 6 Merge 2 4 5 6 1 Merge 2 5 5 2 6 1 Merge 4 6 Algorithms 2 3 6 1 6 Merge initial sequence CS 8833 3 Merge 4 Merge 2 3 2 6

Recurrence for Divide and Conquer Algorithms CS 8833 Algorithms

Recurrence for Merge Sort CS 8833 Algorithms