Algorithms in Action Max Cut using Semidefinite Programming

Algorithms in Action Max Cut using Semidefinite Programming Haim Kaplan, Uri Zwick Tel Aviv University May 2016 Last updated: June 5, 2016 1

Positive Semidefinite (PSD) Matrices •

Positive Semidefinite Programming Can be approximated using multiplicative updates. Interesting application: Approximation algorithm for MAX CUT

Linear Semidefinite Programming Can be solved exactly in polynomial time Can be solved almost exactly in polynomial time

LP/SDP algorithms • Simplex method (LP only) • Ellipsoid method • Interior point methods Algorithms work well in practice, not only in theory! Even faster approximation algorithms using multiplicative weights updates.

Semidefinite Programming (Equivalent formulation – Vector Programming)

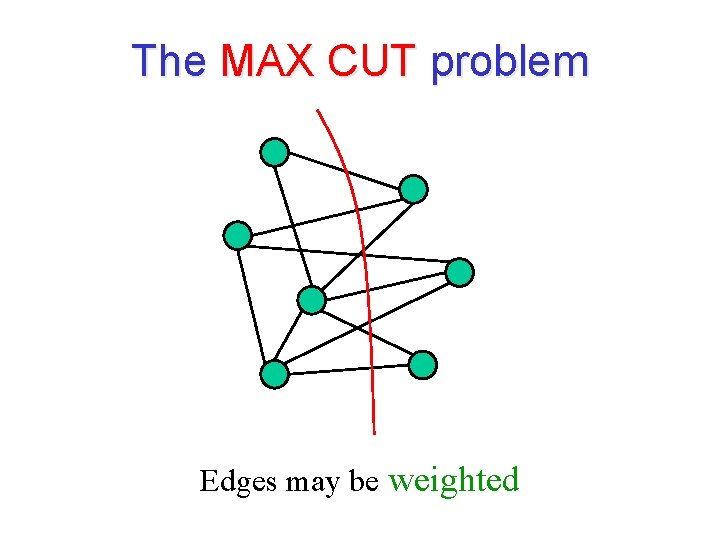
The MAX CUT problem Edges may be weighted

The MAX CUT problem: motivation

A quadratic integer programming formulation of MAX CUT Left side of the cut Right side of the cut

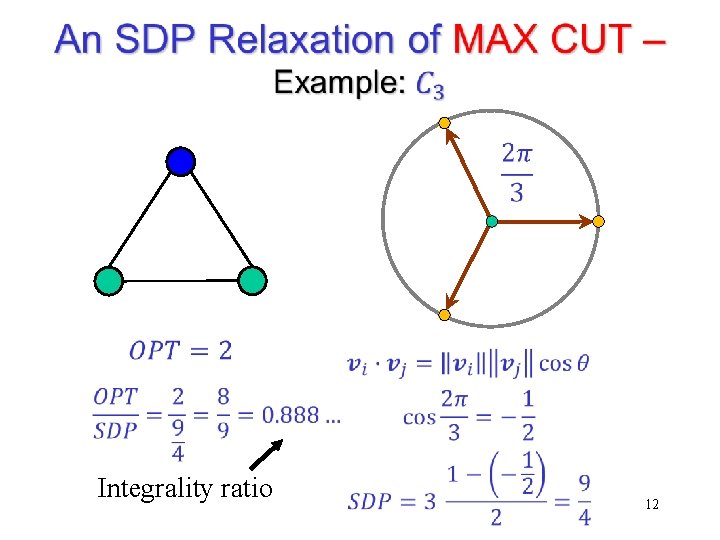
An SDP Relaxation of MAX CUT [Delorme-Poljak (1993)] [Goemans-Williamson (1995)] This is an SDP, and hence can be solved in polynomial time. The optimal value of the SDP gives an upper bound on the weight of the maximum cut. Can we use an optimal solution of the relaxation to obtain a heavy cut?

An SDP Relaxation of MAX CUT – Geometric intuition

Integrality ratio 12

Integrality ratio 13

Random hyperplane rounding [Goemans-Williamson (1995)] Choose a random hyperplane passing through the origin. Use the cut defined by the hyperplane!

Choosing a random hyperplane To choose a random hyperplane, choose a random normal vector

The probability that two vectors are separated by a random hyperplane

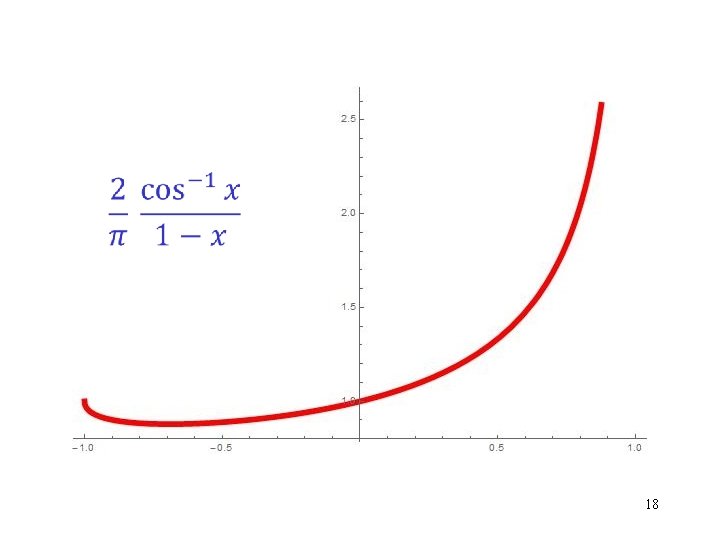
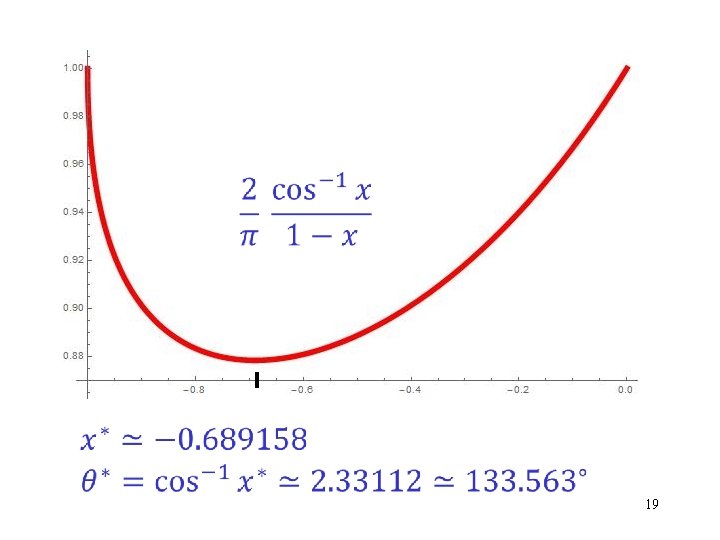
Analysis of the MAX CUT Algorithm [Goemans-Williamson (1995)] Expected weight of the cut obtained using a random hyperplane. Value of the SDP relaxation, which is an upper bound on the weight of an optimal cut. Lower bound on the approximation ratio of the algorithm. 17

18

19

Is the analysis tight? Yes!

The MAX CUT problem: status • Problem is NP-hard • Problem is APX-hard (no PTAS unless P=NP) • Best approximation ratio known, without SDP, is only 0. 5. (Local search, random cut, …) • With SDP, an approximation ratio of 0. 878 can be obtained! [Goemans-Williamson (1995)] • Getting an approximation ratio of 0. 942 is NP-hard! (PCP theorem, … , [Håstad (1997)]) • An approximation ration of 0. 878 is optimal assuming the Unique Games Conjecture [Khot-Kindler-Mossel-O’Donnell (2007)]