Algorithms From the Mathematical Perspective Rosen 3 1

Algorithms From the Mathematical Perspective Rosen 3. 1 Creative Commons License – Curt Hill

What is an Algorithm? • Algorithm: A prescribed set of welldefined rules and processes for solving a problem in a finite number of steps • Prescribed: known in advance • Well defined: unambiguous, clear • Finite: always ends • Not every computer program implements an algorithm, but most do Creative Commons License – Curt Hill

Properties • An algorithm should demonstrate several properties: • Input – they take some type of input data • Output – they produce some answer • Definiteness – each step is unambiguously defined • Correctness – a correct algorithm produces correct results for each set of input values Creative Commons License – Curt Hill

More Properties • Finiteness – always finishes in a finite number of steps – Finite may be large – Recall the halting problem which determines whether finite or not • Effectiveness - it must be possible to perform each step exactly in a finite amount of time • Generality – it should solve the problem for any set of inputs, not just a particular set – We are allowed to limit input domains Creative Commons License – Curt Hill

Expression • How do we represent an algorithm? • Almost every program implements an algorithm – We do not necessarily want to learn each programming language • Choose a standard language – ACM chose ALGOL as their standard – Before that FORTRAN was common • Other possibilities exist Creative Commons License – Curt Hill

Pseudo Code • The book, among others, has chosen pseudo-code • This has greater precision than natural language, yet we do not worry about the syntactical details of a real programming language • The book’s choice looks much like Pascal, which is also a descendent of ALGOL • An appendix of the book describes pseudo-code Creative Commons License – Curt Hill

Rules(? ) of Pseudo code – No need to declare variables, except in procedure headers – No need for ; to terminate or separate a statement – Usually, one statement per line – Indentation is significant – Assignment statement uses : = – Reserved words are bold – An if statement has a then or then and else – Simplified for and while syntax – Comments in braces Creative Commons License – Curt Hill

Example • Find maximum element in sequence: procedure max(a 1, a 2, …an: integer) max : = a 1 {Assignment on name} for i=2 to n if max < ai then max : = ai return max {All done} Creative Commons License – Curt Hill

Searching • Something we do a lot of in Computer Science • We have a collection of items • We want to find whether a given one exists in the collection • Sometimes we search for a key and want the associated data – Account number and account information • Other times just to see if the value exists – such as set membership Creative Commons License – Curt Hill

Two Searches • A linear search looks sequentially through a sequence of values – The search length is proportional to the number of items • A binary search looks through a sorted sequence of values – This works much faster – Proportional to log 2 N Creative Commons License – Curt Hill

Linear procedure linear search(x: integer, a 1, a 2, …, an: distinct integers) i : = 1 while (i ≤ n and x ≠ ai) i : = i + 1 if i ≤ n then location : = i else location : = 0 return location{location is the subscript of the term that equals x, or is 0 if x is not found} Creative Commons License – Curt Hill

Binary procedure binary search(x: integer, a 1, a 2, …, an: increasing integers) i : = 1 {i is the left endpoint of interval} j : = n {j is right endpoint of interval} while i < j m : = ⌊(i + j)/2⌋ if x > am then i : = m + 1 else j : = m if x = ai then location : = i else location : = 0 return location{location is the subscript i of the term ai equal to x, or 0 if x is not found} Creative Commons License – Curt Hill

Sorting • Another extremely important operation • Put a sequence into ascending or descending order • Look at two here • Bubble • Insertion Creative Commons License – Curt Hill

Bubble Sort • • • Basic idea Start at top Compare adjacent elements Exchange if out of order Repeat until a pass has no exchanges See the text for pseudo code Creative Commons License – Curt Hill

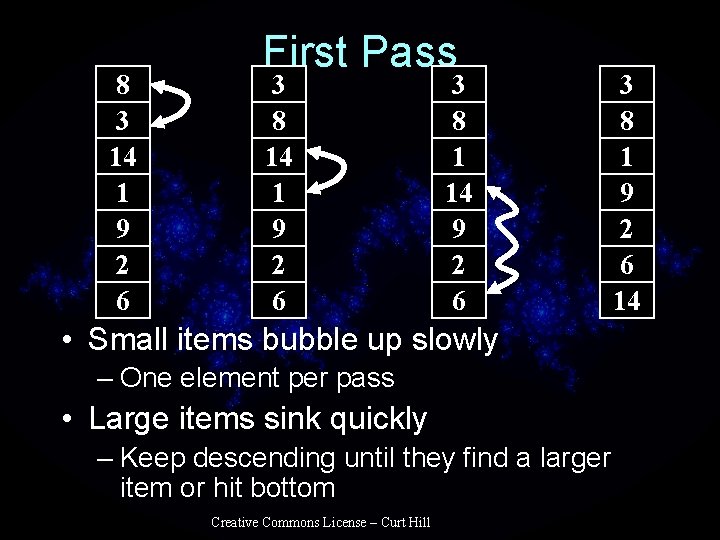
8 3 14 1 9 2 6 First Pass 3 8 14 1 9 2 6 3 8 1 14 9 2 6 • Small items bubble up slowly – One element per pass • Large items sink quickly – Keep descending until they find a larger item or hit bottom Creative Commons License – Curt Hill 3 8 1 9 2 6 14

Commentary • The book uses two for loops • This is not the best approach • However, the bubble sort is perhaps the worst sort in existence – So it does not matter • The only thing it should be ever considered for is a sequence where there are only slight disorderings Creative Commons License – Curt Hill

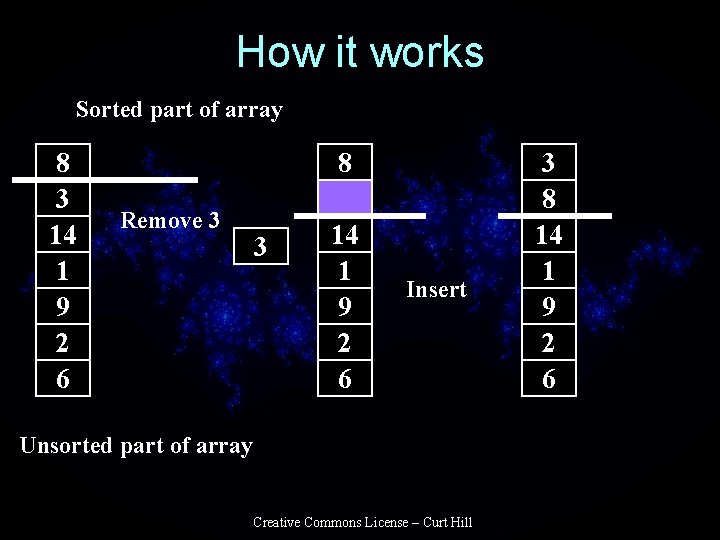
Insertion Sort • Partition the array into two pieces • The first one and all the rest • The first part of the array is already sorted • Remove the first unsorted item • Insert into the correct location of the sorted part Creative Commons License – Curt Hill

How it works Sorted part of array 8 3 14 1 9 2 6 8 Remove 3 3 14 1 9 2 6 Insert Unsorted part of array Creative Commons License – Curt Hill 3 8 14 1 9 2 6

Greedy Algorithms • There a number of situations where we want to find an optimal solution – Usually, a maximum or minimum • There are typically several parameters, that is values that can be changed • Exhaustively searching every combination of every parameter is prohibitively expensive Creative Commons License – Curt Hill

How do they work? • Start at some point – All parameters to function have an arbitrary or given value • Look one step in every direction – Vary each parameter by a small increment • Choose the one that gives the best results and return to the first step with new values • Quit when no more improvement may be made Creative Commons License – Curt Hill

Discussion • There must be a readily available function that produces a measure of the goodness of the solution • The results may be optimal or not depending on the type of problem • As the algorithm homes in on the problem the step size may be adjusted • Next, we will consider the change problem giving the fewest coins Creative Commons License – Curt Hill

Change • Suppose we have to give change • The amount required is in the range 1 to 99 cents • We wish to give the fewest coins • We have the normal coins: quarters, dimes, nickels and pennies • Our function takes the count of each coin and the original change amount and returns how much change is left to be given Creative Commons License – Curt Hill

Greed is good • The starting point is no coins are given – fours counts of zero • We next look at four steps: incrementing each coin • We choose the one that gives us the smallest value that is not negative • This is our best step – next go to the beginning with adjusted parameters Creative Commons License – Curt Hill

Example • Suppose that the amount is 78 cents • We try one of each coin and find that the quarter gets us to 53 • We try one of each again and find that the quarter gets us to 28 • We try one of each again and find that the quarter gets us to 3 • Now the quarter, dime and nickel sends us negative, but 1 penny gets us to 2, which we repeat twice more Creative Commons License – Curt Hill

Commentary • This is a simple with an easy solution • A similar program was shown in 127/160 that solves this optimally but is not a classic greedy • However, greedy solutions work in much more complicated environments where the correct path is not known in advance • The book also observes that if nickels are not available this algorithm will not necessarily be optimal Creative Commons License – Curt Hill

The Halting Problem • This is important because of the finite number of steps requirement of an algorithm • That it is unsolvable shows absolute limitations to static analysis – What can be seen without running a program – It also proves the existence of unsolvable problems • We saw the proof in chapter 1 presentations Creative Commons License – Curt Hill

Exercises • 3. 1 – 3, 7, 19, 35, 53, 55 Creative Commons License – Curt Hill