Algorithms for the Maximum Subarray Problem Based on

Algorithms for the Maximum Subarray Problem Based on Matrix Multiplication Authours：Hisao Tamaki & Takeshi Tokuyama Speaker：Rung-Ren Lin

Outline u Introduction u ½-approximation u Funny matrix multiplication u Reduction u Two little programs

u Introduction u ½-approximation u Funny matrix multiplication u Reduction u Two little programs

Definition u Given an m by n matrix, output the maximum subarray.

History u Bentley proposes this problem in 1984. u Kadane’s algorithm solves 1 -D problem in linear time. u Kadane’s idea does not work for the 2 -D case. u There’s an O(m 2 n) algorithm by using Kadane’s idea.

Kadane’s algorithm i S(i) = A(i) + max{S(i-1), 0}

Preprocessing u Given a matrix A[1…m][1…n], we can compute B[1…m][1…n] in O(mn) time such that B[i][j] represents the sum of A[1…i][1…j].

u Introduction u ½-approximation u Funny matrix multiplication u Reduction u Two little programs

m n Time = mn/2 * 2 = mn

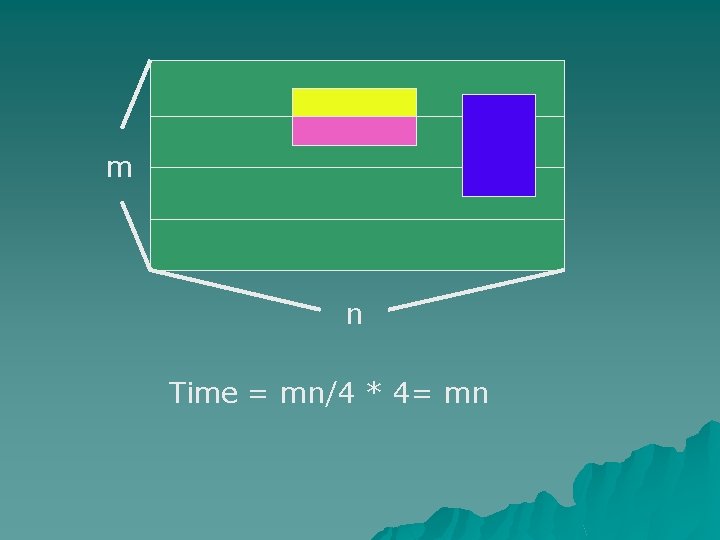
m n Time = mn/4 * 4= mn

Time Complexity u O(mn*logm)

u Introduction u ½-approximation u Funny matrix multiplication u Reduction u Two little programs

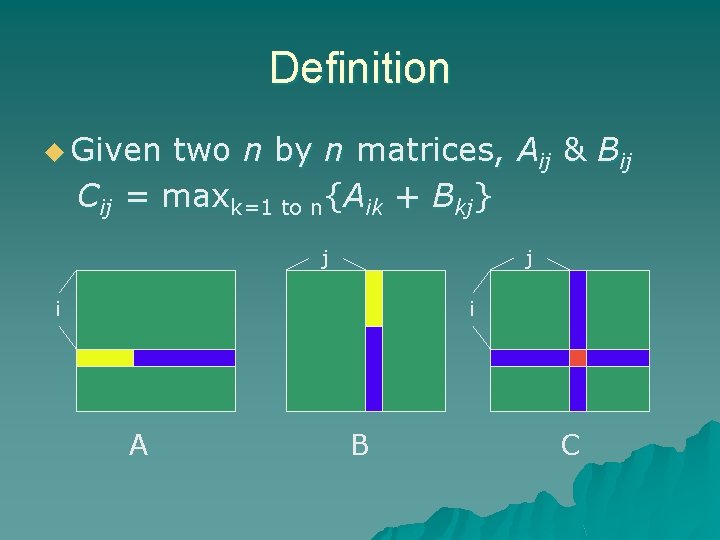
Definition u Given two n by n matrices, Aij & Bij Cij = maxk=1 to n{Aik + Bkj} j j i i A B C

History u Funny matrix multiplication is wellstudied, since its computational complexity is known to be equivalent to that of “all-pairs shortest paths”. u Fredman constructs a subcubic algorithm with running time：

Cont’d u Takaoka in 1992. improved to

u Introduction u ½-approximation u Funny matrix multiplication u Reduction u Two little programs

Definition u T (m , n)：computing time for the m by n matrix u Trow(m, n)：row-centered u Tcol(m, n)：column-centered T(m, n) = Trow(m, n) + Tcol(m, n) + 4 T(m/2, n/2)

Cont’d u Tcenter(m, n)：row & column-centered Trow(m, n) = Tcenter(m, n) + 2 Trow(m, n/2) Tcol(m, n) = Tcenter(m, n) + 2 Tcol(m/2, n)

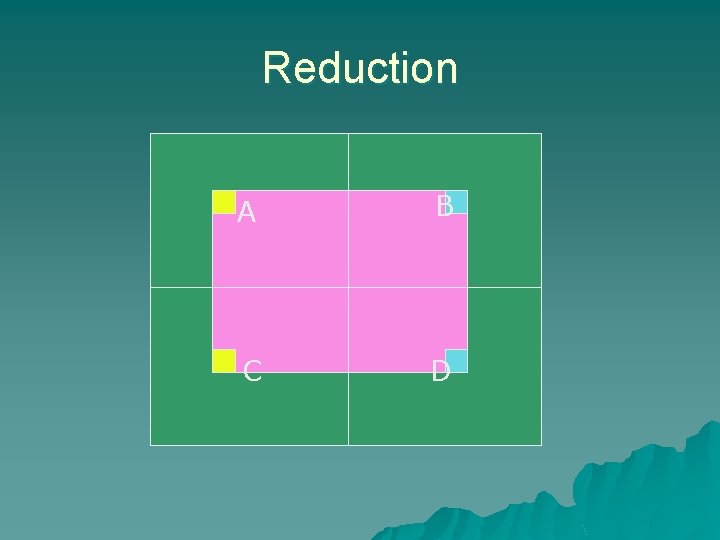
Reduction A B C D

Cont’d u Let A, B, C, D[1…m/2][1…n/2] be the sum of the given area. Xij = maxk=1 to m/2{Aik + Cjk} Yij = maxk=1 to m/2{Bik + Djk} output = max{Xij + Yij}

u Introduction u ½-approximation u Funny matrix multiplication u Reduction u Two little programs

13 -card

Pacman

Challenges u It’s difficult to search 3 -D models.

The End