Algorithms for Solar Active Region Identification and Tracking

Algorithms for Solar Active Region Identification and Tracking Michael Turmon JPL/Caltech Work with Todd Hoeksema, Xudong Sun (Stanford), Harrison Jones, Elena Malanushenko (NSO), Judit Pap (GSFC)

Capabilities Discussed Here Identification – – Label active pixels in multivariate images, e. g. : (LOS B, Ic) There exists a family of methods by many researchers Largely a solved problem for active regions in photosphere Bayesian approach maximizing posterior probability of labeling • Has been released for HMI on jsoc. stanford. edu Tracking – – Grouping of active pixels in labeling into ARs Then, link identified ARs through a series of images Single-link most likely tracker (optimization-based association) Nearing release for HMI as hmi. Mharp_720 s 2

Motivation Allow scientists in to understand great volumes of spatio-temporal data in directly informative terms Identification Tracking Object analysis • Identification: Find objects in multispectral images • Tracking: Link identified objects across a series of images • Object Analysis: Model and classify object tracks Move beyond looking at pixels to understanding phenomena

Identification 4

Identification: Finding the Best Labeling • Bayesian approach: maximize posterior probability having two terms – Trade off fidelity to data (first term) vs. spatial coherence (second) log Pr(class mask | obs. images) = constant + log Pr(obs. images | class mask) + log Pr(class mask) • Likelihood: Probability of a certain observed (field, intensity) given activity type: e. g. , quiet Sun, facula, sunspot – Gaussian mixture model to parameterize each conditional density • Prior: Enforces spatial smoothness of labeling to disambiguate cases near the class boundary – Nearby-neighbor smoothness via Markov random field (MRF) model • Find mask via discrete optimization of posterior w. r. t. entire labeling 5

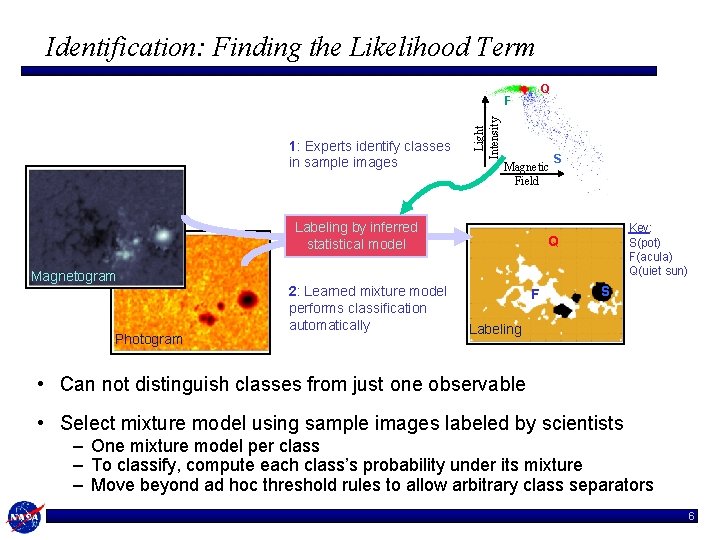
Identification: Finding the Likelihood Term Q 1: Experts identify classes in sample images Light Intensity F Magnetic Field Labeling by inferred statistical model Magnetogram Photogram 2: Learned mixture model performs classification automatically S Key: S(pot) F(acula) Q(uiet sun) Q F N Q S S Labeling • Can not distinguish classes from just one observable • Select mixture model using sample images labeled by scientists – One mixture model per class – To classify, compute each class’s probability under its mixture – Move beyond ad hoc threshold rules to allow arbitrary class separators 6

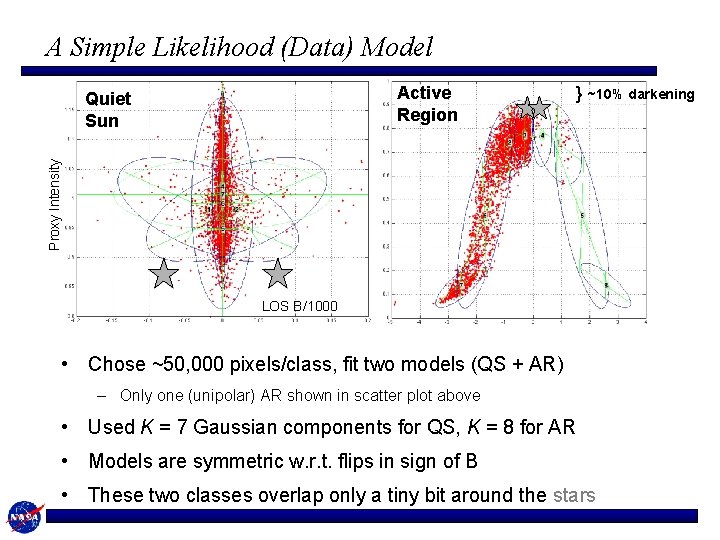
A Simple Likelihood (Data) Model Active Region } ~10% darkening Proxy Intensity Quiet Sun LOS B/1000 • Chose ~50, 000 pixels/class, fit two models (QS + AR) – Only one (unipolar) AR shown in scatter plot above • Used K = 7 Gaussian components for QS, K = 8 for AR • Models are symmetric w. r. t. flips in sign of B • These two classes overlap only a tiny bit around the stars

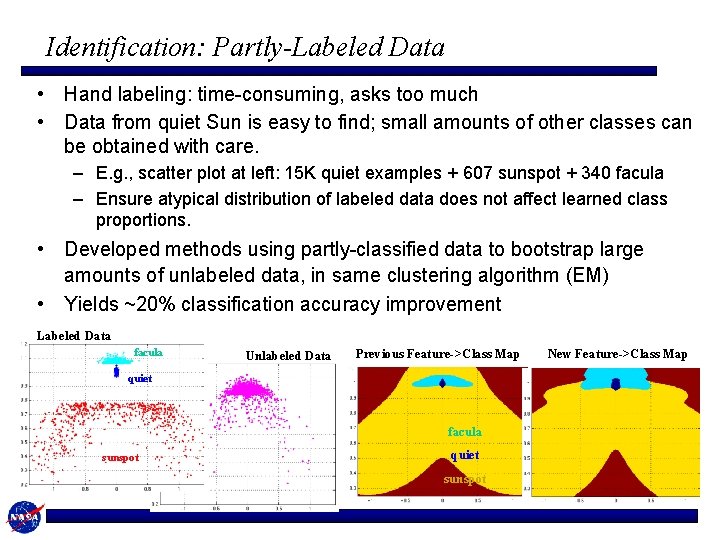
Identification: Partly-Labeled Data • Hand labeling: time-consuming, asks too much • Data from quiet Sun is easy to find; small amounts of other classes can be obtained with care. – E. g. , scatter plot at left: 15 K quiet examples + 607 sunspot + 340 facula – Ensure atypical distribution of labeled data does not affect learned class proportions. • Developed methods using partly-classified data to bootstrap large amounts of unlabeled data, in same clustering algorithm (EM) • Yields ~20% classification accuracy improvement Labeled Data facula Unlabeled Data Previous Feature->Class Map quiet facula sunspot quiet sunspot New Feature->Class Map

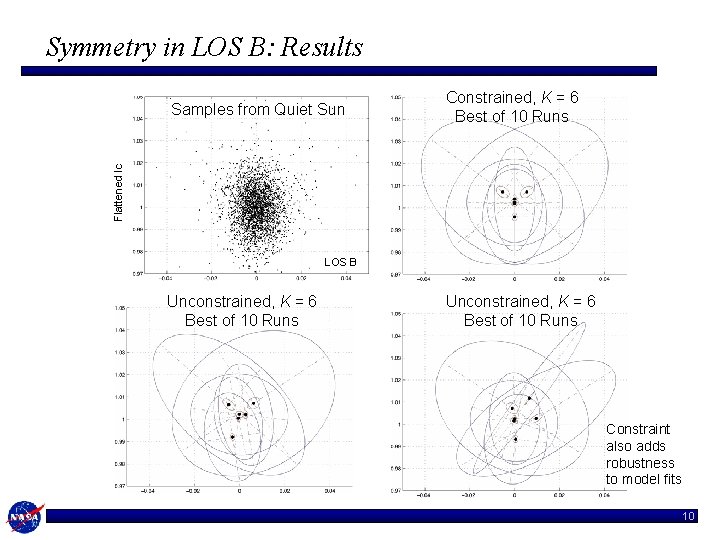
Refinement: Symmetry in LOS B • Data model should be invariant to the sign of LOS B • Distributional constraint, for 2 d observation y: • For a normal mixture M, like our class-conditional likelihoods, the constraint implies: • Modify EM to respect this constraint: Average sufficient statistics over the cyclic groups associated with A. 9

Symmetry in LOS B: Results Constrained, K = 6 Best of 10 Runs Flattened Ic Samples from Quiet Sun LOS B Unconstrained, K = 6 Best of 10 Runs Constraint also adds robustness to model fits 10

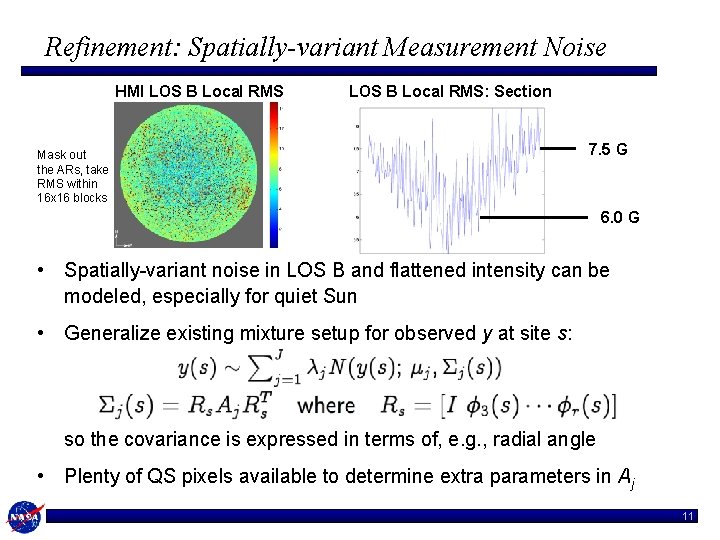
Refinement: Spatially-variant Measurement Noise HMI LOS B Local RMS: Section Mask out the ARs, take RMS within 16 x 16 blocks 7. 5 G 6. 0 G • Spatially-variant noise in LOS B and flattened intensity can be modeled, especially for quiet Sun • Generalize existing mixture setup for observed y at site s: so the covariance is expressed in terms of, e. g. , radial angle • Plenty of QS pixels available to determine extra parameters in Aj 11

Refinement: Customizing the Prior • Account for spherical geometry with metric MRF prior • Original prior penalizes all label-conflicts equally: 1 1 1 2 1 1 1 • Modified prior penalizes differently across disk: • Smaller penalties are assigned to farther-off conflicts: where dist(s, s’) = great-circle distance between sites 12

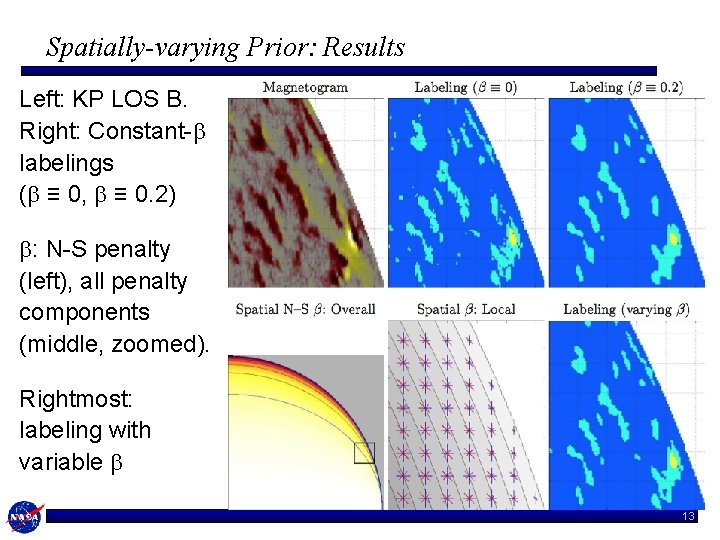
Spatially-varying Prior: Results Left: KP LOS B. Right: Constant-b labelings (b ≡ 0, b ≡ 0. 2) b: N-S penalty (left), all penalty components (middle, zoomed). Rightmost: labeling with variable b 13

HMI Identification Status • Output Masks – Available as hmi. Marmask_720 s and hmi. Marmask_720 s_nrt – Full-disk 4 Kx 4 K mask images in coordinates of observations – Never re-map observed images to find the mask • Further Calibration – Calibration team is working on better removal of limbdarkening and time-dependent flat-field from intensity proxy. – Current HMI region model does not really use the intensity proxy because of limb artifacts. • Enhancements – A more detailed class breakdown is possible. – E. g. , umbra/penumbra were not reliably determined from MDI; believe HMI should be better 14

Tracking 15

Components of “Tracking” • Identification (just discussed) • Grouping – Group separated features into AR – Formal literature on this is not well-developed – Use a simple template-based method • Association – Construct 1: 1 map from previous AR set to next AR set. • Chained together, you have a track. – Criterion: maximize cumulative area of overlap – Heuristics to “look harder” for new or dying ARs • Naming – Link a track to a name like NOAA AR#9077 16

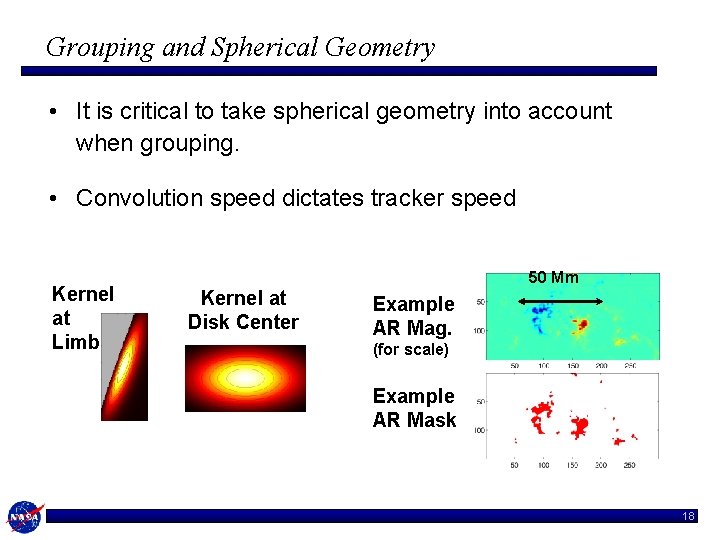
Active Region Tracking: Grouping into ARs • Activity mask = a set of pixels – Grouping into NOAA-like AR’s is not trivial – Connected components insufficient • Take a matched-filter type approach – Convolve AR mask with a Gaussian kernel – Threshold – AR groups are within basins 50 Mm • Devilish Details – Gaussian in 3 D pixel-pixel distance; stretched longitudinally; FWHM ~50 x 25 Mm (~40 x 20 MDI pixel) at disk center – Convolution on sphere to treat the limb fairly – AR masks sparse: fast convolution (HMI: 12 s) – More cleverness is possible, e. g. polarity 17

Grouping and Spherical Geometry • It is critical to take spherical geometry into account when grouping. • Convolution speed dictates tracker speed Kernel at Limb 50 Mm Kernel at Disk Center Example AR Mag. (for scale) Example AR Mask 18

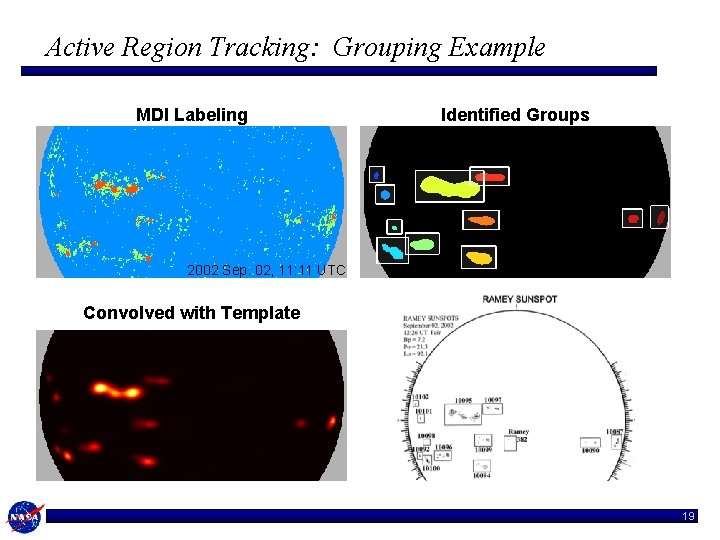
Active Region Tracking: Grouping Example MDI Labeling Identified Groups 2002 Sep. 02, 11: 11 UTC Convolved with Template 19

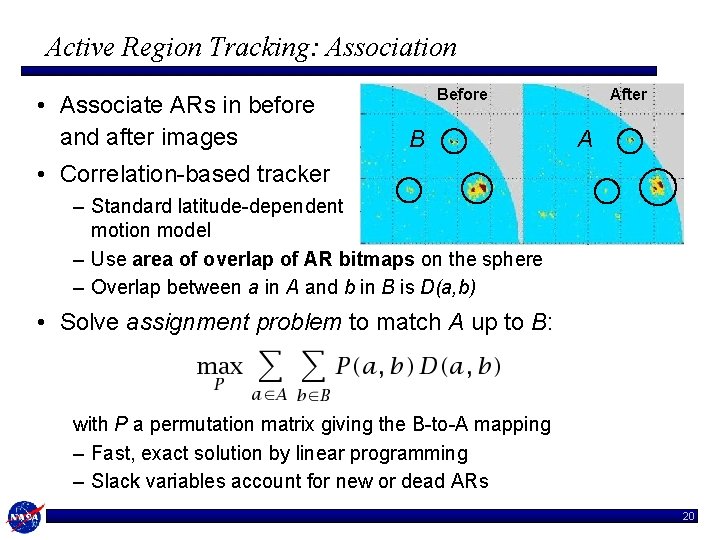
Active Region Tracking: Association • Associate ARs in before and after images Before B After A • Correlation-based tracker – Standard latitude-dependent motion model – Use area of overlap of AR bitmaps on the sphere – Overlap between a in A and b in B is D(a, b) • Solve assignment problem to match A up to B: with P a permutation matrix giving the B-to-A mapping – Fast, exact solution by linear programming – Slack variables account for new or dead ARs 20

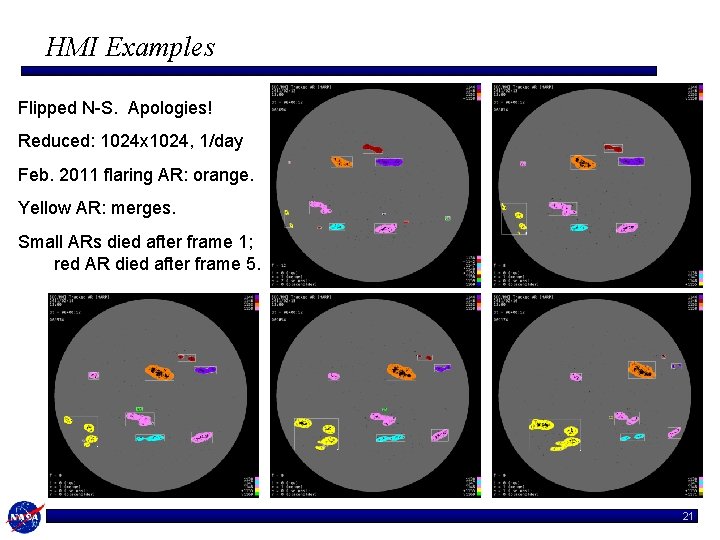
HMI Examples Flipped N-S. Apologies! Reduced: 1024 x 1024, 1/day Feb. 2011 flaring AR: orange. Yellow AR: merges. Small ARs died after frame 1; red AR died after frame 5. 21

22

References M. Turmon, H. Jones, J. Pap, O. Malanushenko, “Statistical feature recognition for multidimensional solar imagery”, Solar Physics, 04/2010. The mixture modeling work appeared in: Mixtures-2001, “Recent Developments in Mixture Modelling, ” Hamburg Compstat-2004, Prague, as “Symmetric Normal Mixtures” Earlier work: J. Pap, H. Jones, M. Turmon & L. Floyd, “Study of the SOHO/VIRGO Irradiance Variations using MDI and Kitt Peak images, ” Proc. SOHO-11 Workshop, Davos, 2002. H. P. Jones, M. Turmon, et al. “A comparison of feature classification methods for modeling solar irradiance variation, ” 34 th COSPAR Scientific Assembly, 2002. The research described here was carried out in part by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. Copyright 2011. All rights reserved. Government sponsorship acknowledged. 23