Algorithms for SAT Based on Search in Hamming

Algorithms for SAT Based on Search in Hamming Balls Author : Evgeny Dantsin, Edward A. Hirsch, and Alexander Wolpert Speaker : 羅正偉

Outline w Definition of SAT problem w Introduction of this paper w Definitions and notation w Randomized Algorithm

Preliminary: K-SAT problem

Preliminary-A fact w 2 -SAT is in P, but 3 -SAT is NP-complete.

Preliminary-Hamming Ball w Definition: The Hamming ball of radius R around a truth assignment A is the set of all assignments whose Hamming distance to A is less than or equal to R. w The assignment A is called the center of the ball. w The volume of a ball is the number of assignments that belong to the ball.

Introduction w In this paper a randomized algorithm for SAT is given, and its derandomized version is the first non-trivial bound for a deterministic SAT algorithm with no restriction on clause length. w For k-SAT, Schuler’s algorithm is better than this one.

Notation

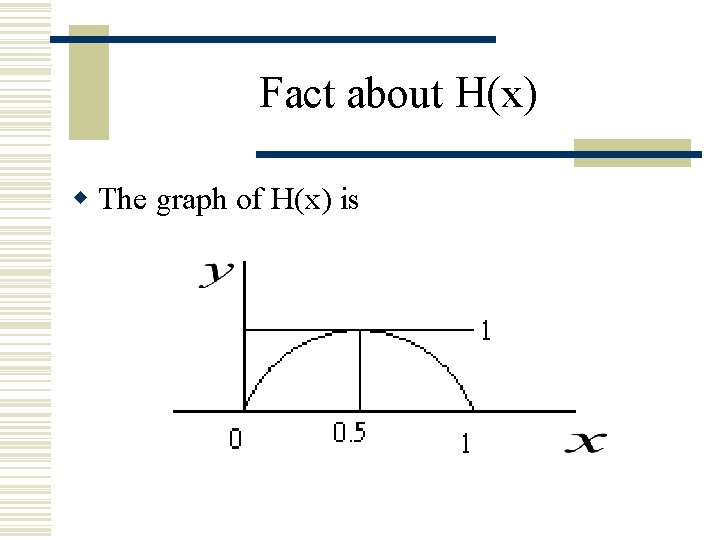
Fact about H(x) w The graph of H(x) is

A bound of V(n, R)

Randomized Algorithm w The randomized algorithm is called Random. Balls, and it invokes procedures called Ball. Checking and Full-Ball-Checking.

Ball-Checking algorithms

Observations w The recursion depth is at most R w Any literal is altered at most once during execution of Ball-Checking, and at any time, those remaining variables are assigned as in the original assignment

Lemma 1 w There is a satisfying assignment in B(A, R) iff Ball-Checking(F, A, R) returns a satisfying assignment in B(A, R) w Proof. By induction of R (see reference)

Lemma 2 w The running time of Ball-Checking(F, A, R) is at most , where k is the maximum length of clauses occurring at step 3 in all recursive calls. w Proof. The recursion depth is at most R and the maximum degree of branching is at most k.

Full Ball Checking w Procedure Full-Ball-Checking(F, A, R) Input: formula F over variables , assignment A, number R Output: satisfying assignment or “no” w 1. Try each assignment A’ in B(A, R), if it satisfies F, return it. w 2. Return “no”

Observation w Full-Ball-Checking runs in time poly(n)m. V(n, R)

Randomized algorithm

Lemma 3 w Correctness of Random-Balls. For any R, l, the following holds: (a)If F is unsatisfiable, then Random-Balls returns “no”, (b)else Random-Balls finds a satisfying assignment with probabability 1/2

Proofs of lemma 3

REVIEW!! A bound of V(n, R)

Probability of correctness w So the prob. of correctness = 1 – 1/e > 1/2 w Choosing N to be k times larger will reduce the probability of error to less than. w Note this doesn’t ruin the time complexity we need.

Lemma 4 w Consider the execution of Random. Balls(F, R, l) that invokes Ball-Checking. For any input R, l, the maximum length of clauses chosen at step 3 of Procedure Ball. Checking is less than l.

REVIEW!! Ball-Checking algorithms

Proof of lemma 4

Lemma 5 w For any R, l, let p be the probability (taken over random assignment A) that Random. Balls invokes Full-Ball-Checking. Then

Proof of lemma 5

Proof of lemma 5(conti. )

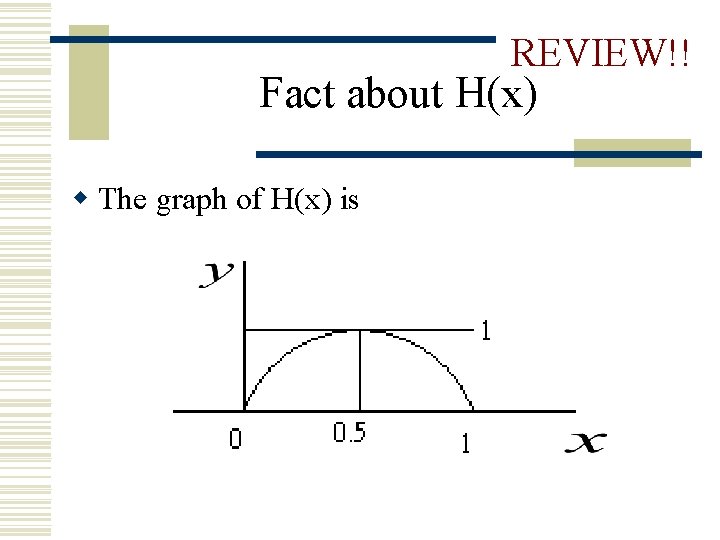
REVIEW!! Fact about H(x) w The graph of H(x) is

Theorem 1

Proof of theorem 1

Proof of Theorem 1(conti. )

Proof of Theorem 1 (conti. ) w Assign R=a , l=b , where a < b constants. We use the fact ln(1+x)=x+o(x).

Proof of theorem 1(conti. )

Proof of Theorem 1 (conti. ) w Taking a=0. 339, b=1. 87, we have Φ , ψ>0. 712 , proving theorem.

Reference w E. Dantsin, A. Goerdt, E. A. Hirsch, R. Kannan, J. Kleinberg, C. Papadimitriou, P. Raghavan, and U. Schoning. A deterministic algorithm for K-SAT based on local search. Theoretical Computer Science, 289(1): 69 -83, October 2002.