Algorithms for hard problems Parameterized complexity definitions sample

Algorithms for hard problems Parameterized complexity – definitions, sample algorithms Juris Viksna, 2020
![Parameterized complexity Combinatorial "explosion" for NP-hard problems [Adapted from R. Downey and M. Fellows] Parameterized complexity Combinatorial "explosion" for NP-hard problems [Adapted from R. Downey and M. Fellows]](http://slidetodoc.com/presentation_image_h2/947da80e9cd0f092fbed5c92df64963c/image-2.jpg)
Parameterized complexity Combinatorial "explosion" for NP-hard problems [Adapted from R. Downey and M. Fellows]
![Parameterized complexity attempts to confine combinatorial "explosion" [Adapted from R. Downey and M. Fellows] Parameterized complexity attempts to confine combinatorial "explosion" [Adapted from R. Downey and M. Fellows]](http://slidetodoc.com/presentation_image_h2/947da80e9cd0f092fbed5c92df64963c/image-3.jpg)
Parameterized complexity attempts to confine combinatorial "explosion" [Adapted from R. Downey and M. Fellows]

Parameterized complexity - Definitions Definition (FPT) A parametrized problem L * * is Fixed Parameter Tractable if there is an algorithm that for input (x, y) * * with |x| = k and |y| = n decides whether (x, y) L in time f(k) n , where f is an arbitrary function and is a constant. Definition does not change if f(k) n is replaced by f(k) + n (!)

Parameterized complexity - Definitions Mk for every n solves the problem in time f(k) n For each k there is a constant ck, such that f(k) n > n + 1 for n ck M'k: - simulates Mk for n ck - looks up value from the table for n ck M'k solves the problem in time f(k) ck + n a+1
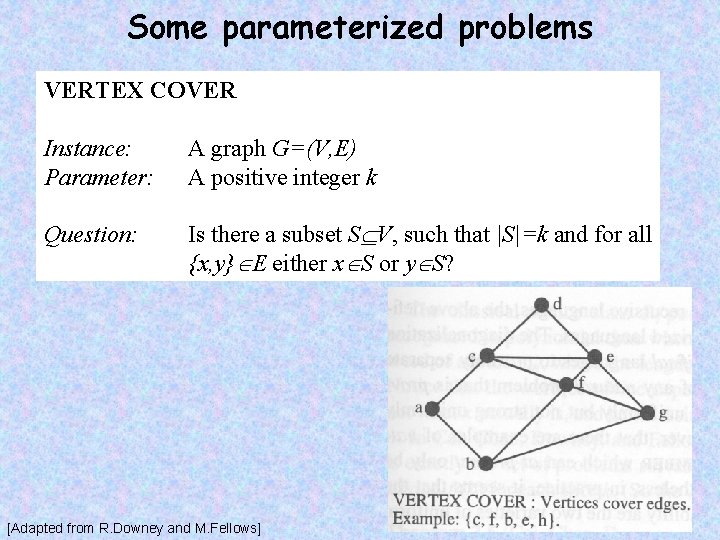
Some parameterized problems VERTEX COVER Instance: Parameter: A graph G=(V, E) A positive integer k Question: Is there a subset S V, such that |S|=k and for all {x, y} E either x S or y S? [Adapted from R. Downey and M. Fellows]
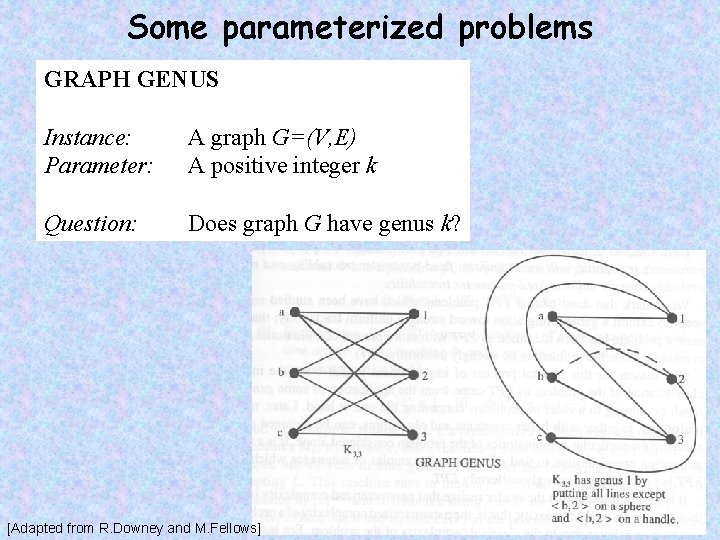
Some parameterized problems GRAPH GENUS Instance: Parameter: A graph G=(V, E) A positive integer k Question: Does graph G have genus k? [Adapted from R. Downey and M. Fellows]

Some parameterized problems GRAPH LINKING NUMBER Instance: Parameter: A graph G=(V, E) A positive integer k Question: Can G be embedded in 3 -space such that the maximum size of a collection of topologically linked disjoint cycles is bounded by k? [Adapted from R. Downey and M. Fellows]

Some parameterized problems VERTEX COVER: A single algorithm G running in time 2 k |G| for each k [Downey and Fellows 1992] GRAPH GENUS: A single algorithm F, which for each fixed k determines whether graph G has genus k in time O(|G|3) [Fellows and Langston 1988] GRAPH LINKING NUMBER: For each k there is an algorithm k, which determines whether graph G has linking number k in time O(|G|3) [Fellows and Langston 1988]

Parameterized complexity - Definitions A problem L is uniformly FPT, if there is an algorithm F, a constant c and a function f, such that: - the running time of F(‹x, k›) is at most f(k)|x|c - ‹x, k› A iff F(‹x, k›) = 1. A problem L is strongly uniformly FPT, if L is uniformly FPT via some F and f, such that f is recursive. A problem L is nonuniformly FPT if there is a constant c, a function f and a collection of algorithms {Fk}k N, such that for each k: - the running time of Fk(‹x, k›) is at most f(k)|x|c - ‹x, k› A iff Fk(‹x, k›) = 1.

"klam" values Algorithms for VERTEX Tower of 2's of height described by tower of 2's of height described by COVER: tower of 2's. . . (impractical even for k = 1 : ) • O(f(k) n 3) [Fellows, Langston 1986] • O(f(k) n 2) [Johnson, 1987] 500 k 2 2 FPT if solvable in time f(k)+nc klam value - the largest k for which f(k) is less that some universal "speed limit" U (e. g. U= 1020) [Adapted from R. Downey and M. Fellows]

Parameterized complexity • Parametrized tractability (methods for constructing FPT algorithms) • Parametrized intractability (how to "prove" that there are no FPT algorithm for a given problem)

Bounded search tree methods • First, construct a search space (tree), such that the size search space depends only from parameter k • Then run some relatively efficient algorithm (say DFS) on each branch of the tree For fixed k search space is of constant size, thus we obtain a FPT algorithm
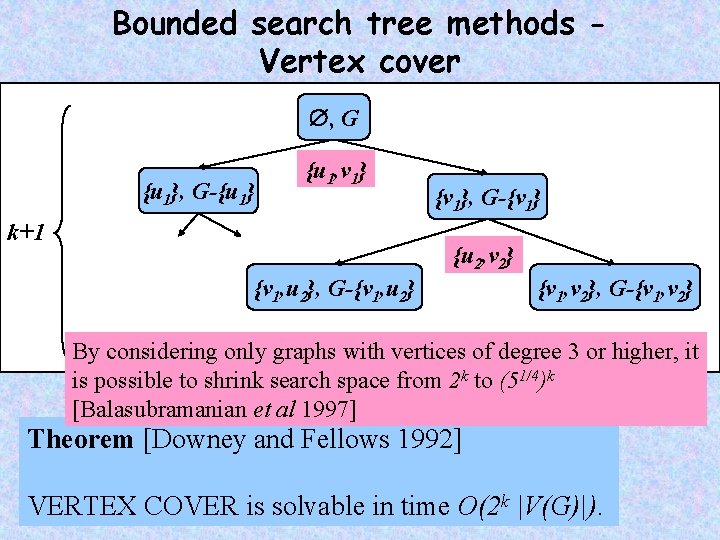
Bounded search tree methods Vertex cover , G {u 1}, G-{u 1} {u 1, v 1} k+1 {v 1}, G-{v 1} {u 2, v 2} {v 1, u 2}, G-{v 1, u 2} {v 1, v 2}, G-{v 1, v 2} By considering only graphs with vertices of degree 3 or higher, it is possible to shrink search space from 2 k to (51/4)k [Balasubramanian et al 1997] Theorem [Downey and Fellows 1992] VERTEX COVER is solvable in time O(2 k |V(G)|).

Kernel methods The main idea of the reduction to problem kernel is to reduce a problem instance I to an equivalent instance I', where the size of I' is bounded by some function of the parameter k. The instance I' is then exhaustively analyzed, and a solution for I' lifted to a solution to I. Usually this will give and additive rather that multiplicative f(k) exponential factor
![Kernel methods - Vertex cover Theorem [Buss 1989] VERTEX COVER is solvable in time Kernel methods - Vertex cover Theorem [Buss 1989] VERTEX COVER is solvable in time](http://slidetodoc.com/presentation_image_h2/947da80e9cd0f092fbed5c92df64963c/image-16.jpg)
Kernel methods - Vertex cover Theorem [Buss 1989] VERTEX COVER is solvable in time O(k 2 k + k |V(G)|). Observation Any vertex of degree greater than k must belong to every k-element vertex cover. Step 1 Locate all vertices in G of degree greater than k; let p equal the number of such vertices. If p > k, there is no k-vertex cover. Otherwise let k' = k – p. Step 2 Discard all vertices found in step 1 and the edges incident to them. If the resulting graph G' has more than k'(k+1) vertices, reject.

Kernel methods - Vertex cover Observation Any vertex of degree greater than k must belong to every k-element vertex cover. Graph with k' vertex cover and vertex degree bounded by k has up to k'(k+1) vertices Step 1 Locate all vertices in G of degree greater than k; let p equal the number of such vertices. If p > k, there is no k-vertex cover. Otherwise let k' = k – p. Step 2 Discard all vertices found in step 1 and the edges incident to them. If the resulting graph G' has more than k'(k+1) vertices, reject. Doable in O(k 2 k) time Step 3 If G' has no k'-vertex cover, reject. Otherwise, any k'-vertex cover of G' plus the p vertices from step 1 constitutes a k-vertex cover for G.

Kernel methods - Vertex cover Kernel method Search tree method O(k 2 k + k |V(G)|) O(2 k |V(G)|) O((51/4)k |V(G)|) If we use reduction to problem kernel first, and then apply search tree method to problem kernel, we improve additive bounds to: O(kn + 2 kk 2) [Balasubramanian et al 1992] O(kn + ((51/4)kk 2) [Balasubramanian et al 1992]

Closest string problem

Closest string problem

Closest string problem
- Slides: 21