Algorithms for hard problems Introduction Juris Viksna 2020

Algorithms for hard problems Introduction Juris Viksna, 2020

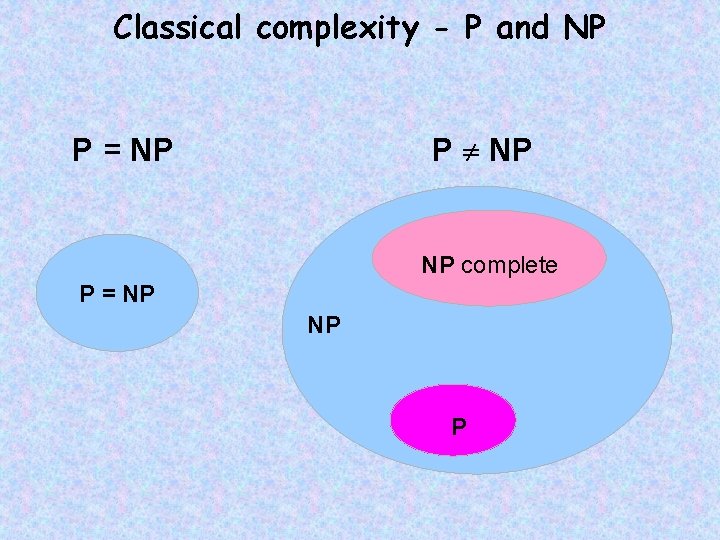
Classical complexity - P and NP P = NP NP complete P = NP NP P

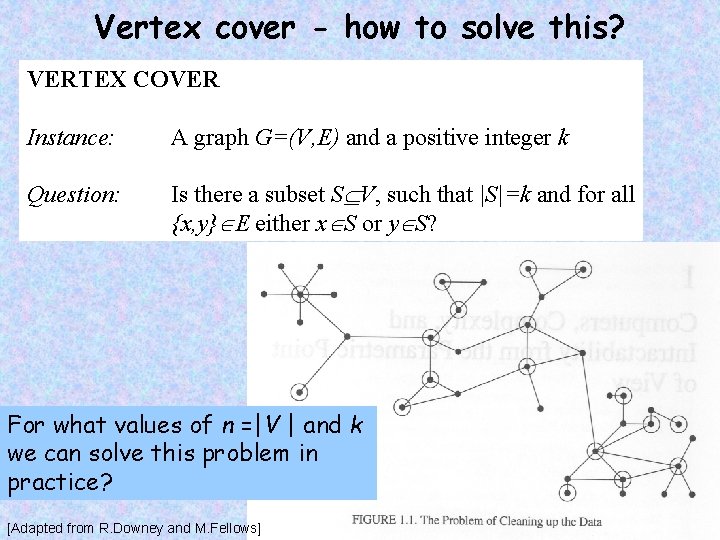
Vertex cover - how to solve this? VERTEX COVER Instance: A graph G=(V, E) and a positive integer k Question: Is there a subset S V, such that |S|=k and for all {x, y} E either x S or y S? For what values of n =|V | and k we can solve this problem in practice? [Adapted from R. Downey and M. Fellows]

Vertex cover - how to solve this? A "universal" approach: - problem is in NP, so we can try to search through all possible witnesses that vertex cover of the given size exists - the running time is nk, thus for n=100 we could probably deal with k<7 and for n=1000 with k<5. . . Can we do better?

Approaches to NP-hard problems • Branch-and-bound algorithms • Heuristic methods • Approximation algorithms • Probabilistic algorithms • Pseudo-polynomial algorithms • FPT algorithms

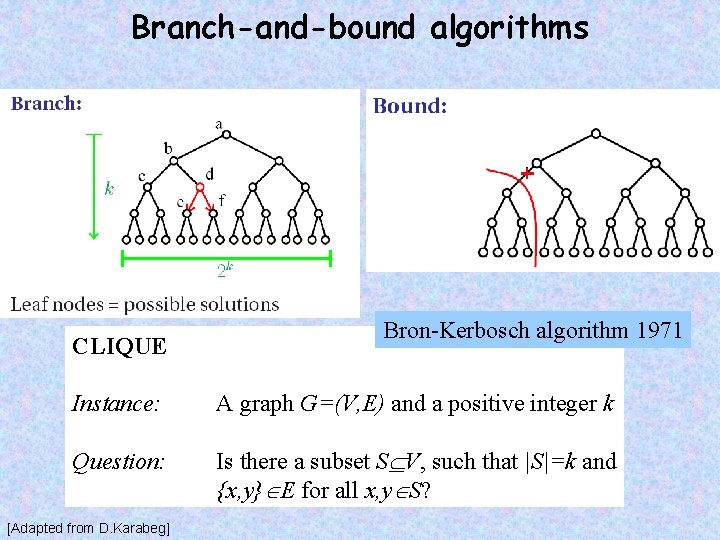
Branch-and-bound algorithms CLIQUE Bron-Kerbosch algorithm 1971 Instance: A graph G=(V, E) and a positive integer k Question: Is there a subset S V, such that |S|=k and {x, y} E for all x, y S? [Adapted from D. Karabeg]

Heuristic methods TSP (TRAVELING SALESMAN PROBLEM) Instance: Problem: A complete graph G=(V, E) with edge weights w: E R+ Find a cycle of minimum cost containing each of the vertices exactly once. Note, that in this case we consider an optimization problem and not a decision problem

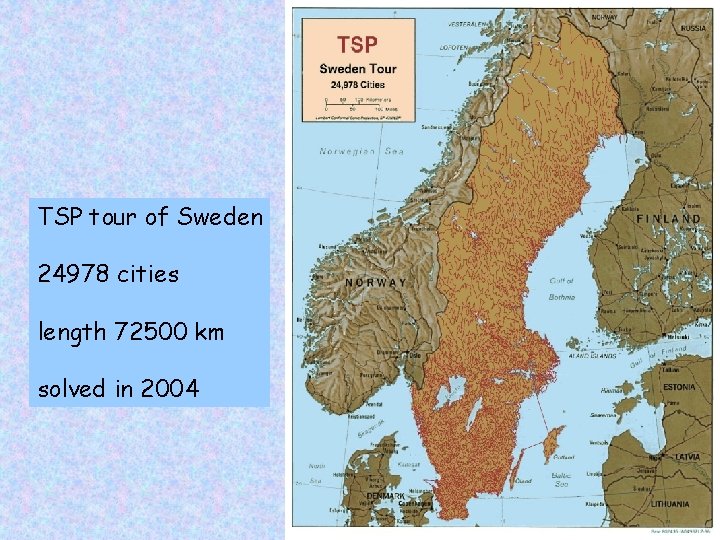
Heuristic methods TSP tour of Sweden 24978 cities length 72500 km solved in 2004

Heuristic methods Idea - use a state space search algorithm (A*) with some reasonable heuristic: - states: partially completed cycles - production rules: all possible extensions of a partial cycle by adding one edge - if heuristic h will not exceed the minimum weight of extension to completed cycle, then A* guarantees to find an optimal solution (!)

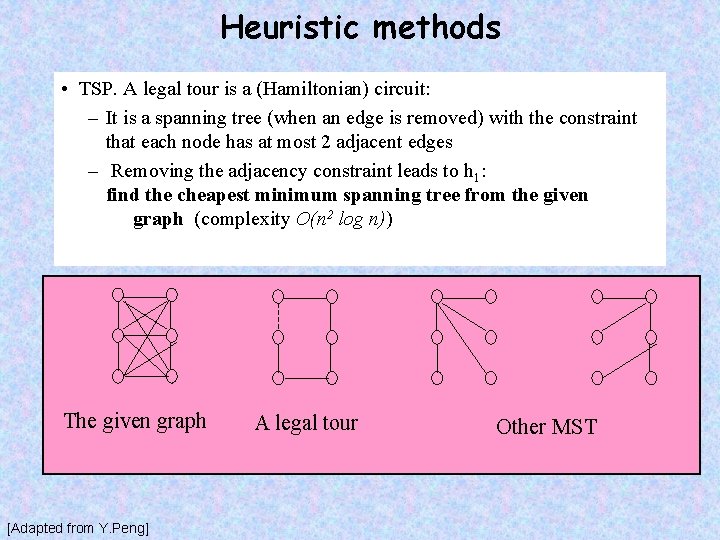
Heuristic methods • TSP. A legal tour is a (Hamiltonian) circuit: – It is a spanning tree (when an edge is removed) with the constraint that each node has at most 2 adjacent edges – Removing the adjacency constraint leads to h 1: find the cheapest minimum spanning tree from the given graph (complexity O(n 2 log n)) The given graph [Adapted from Y. Peng] A legal tour Other MST

Heuristic methods • TSP. A legal tour is a (Hamiltonian) circuit: – It is a connected second degree graph (each node has exactly two adjacent edges) – Removing the connectivity constraint leads to h 2: find the cheapest second degree graph from the given graph (complexity O(n 3)) The given complete graph [Adapted from Y. Peng] A legal tour Other second degree graphs

Approximation algorithms VERTEX COVER Instance: A graph G=(V, E) Find a largest subset S V, such for all {x, y} E either x S or y S? Again, here we consider an optimization problem Problem: Approximation algorithm for VERTEX COVER problem: S E E[G] while E let (u, v) be am arbitrary edge in E S S {u, v} remove from E every edge incident on either u or v return S

Approximation algorithms Approximation algorithm for VERTEX COVER problem: S E E[G] while E let (u, v) be am arbitrary edge in E S S {u, v} remove from E every edge incident on either u or v return S [Adapted from T. Cormen et al]

Approximation algorithms Approximation algorithm for VERTEX COVER problem: S E E[G] while E let (u, v) be am arbitrary edge in E S S {u, v} remove from E every edge incident on either u or v return S C* C - the size of vertex cover - the size of set S returned by algorithm From each pair {u, v} added to S at least one vertex should belong to any vertex cover Thus C 2 C* Algorithm finds a 2 -approximation

Approximation algorithms • Let C* be the cost of an optimal solution, and let C be the cost of the solution of an approximation algorithm. The algorithm has an approximation ratio of ρ(n) if, for all solutions max(C/C*, C*/C) ≤ ρ(n). • We say that an approximation algorithm with an approximation ration of ρ(n) is a ρ(n)approximation algorithm. [Adapted from S. Guattery]

Approximation algorithms MAX CUT Instance: A graph G=(V, E) Problem: Split V in 2 disjoint sets V 1 and V 2, such that {{x, y} E | x V 1 and y V 2} is maximal Easy with (n) = 2 [Erdös 1965] NP-hard for (n) = 1. 06 [Arora et al 1992] maximize [Adapted from L. Lovász] Polynomial for (n) = 1. 14 [Goemans, Williamson 1993]

Approximation algorithms • An approximation scheme is an approximation algorithm that takes an instance and an ε > 0, and produces a (1+ε) approximation. • If an approximation scheme runs in polynomial time in both the size its input and ε, we say it is a polynomial-time approximation scheme (PTAS). [Adapted from S. Guattery]

Approximation algorithms KNAPSACK Instance: A finite set A of elements, with a size s: A Z+ and value v: A Z+ for each element, and integer K Problem: Find a subset S A, such that x S s(x) K and x S v(x) is maximal. • There is a PTAS for KNAPSACK problem with a running time O(n 3/ ). • If P ≠ NP, the general TSP problem cannot be approximated within any constant ρ ≥ 1.

Probabilistic algorithms PRIMALITY TESTING Instance: A positive integer n Question: Is n a prime?

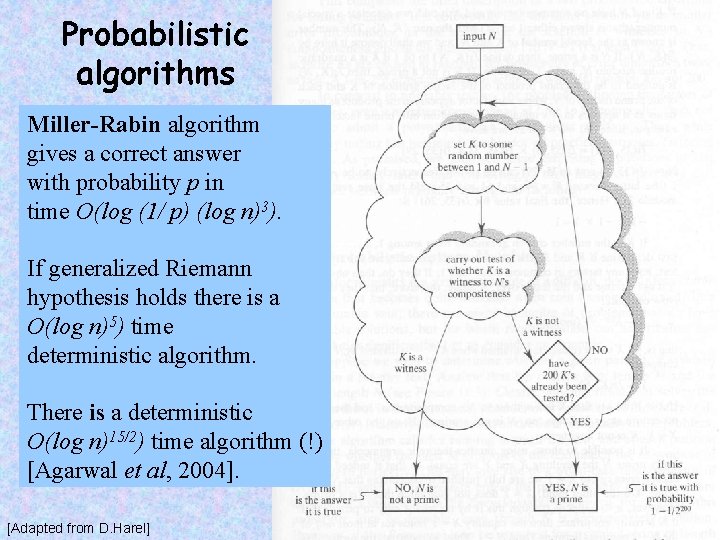
Probabilistic algorithms Miller-Rabin algorithm gives a correct answer with probability p in time O(log (1/ p) (log n)3). If generalized Riemann hypothesis holds there is a O(log n)5) time deterministic algorithm. There is a deterministic O(log n)15/2) time algorithm (!) [Agarwal et al, 2004]. [Adapted from D. Harel]

Pseudo-polynomial algorithms PARTITION Instance: A finite set A={a 1, . . . , an} of positive integers Question: Is there a subset S A, such that x S x = x S x? A dynamic programming algorithm: B = x A x. For i n and j B/2 define T(i, j) to be true if and only if there is a subset Y {a 1, . . . , ai}, such that x Y x = j. Formula: T(i, j) = true iff T(i-1, j)= true or T(i-1, j-ai)= true. Polynomial in n. B (!), but not in n. . .

Pseudo-polynomial algorithms [Adapted from D. Karabeg]

Vertex cover revisited VERTEX COVER Instance: A graph G=(V, E) and a positive integer k Question: Is there a subset S V, such that |S|=k and for all {x, y} E either x S or y S? We already developed time nk algorithm for this problem. . . However, it is possible to do better:

Vertex cover revisited Algorithms for VERTEX COVER: • O(f(k) n 3) [Fellows, Langston 1986] • O(f(k) n 2) [Johnson 1987] • O(2 k n) (polynomial for k=O(log n)) [Fellows 1988] • O(kn + 2 k k 2 k+2) [Buss 1989] • O(kn + 2 k k 2) [Balasubramanian et al 1992] • O(3 k n) [Papadimitriu 1993] • O(kn + (4/3)k k 2) [Balasubramanian et al 1996]

Parametrized complexity Combinatorial "explosion" for NP-hard problems [Adapted from R. Downey and M. Fellows]

Parametrized complexity attempts to confine combinatorial "explosion" [Adapted from R. Downey and M. Fellows]

Parametrized complexity - Definitions Definition (FPT) A parametrized problem L * * is Fixed Parameter Tractable if there is an algorithm that for input (x, y) * * with |x| = k and |y| = n decides whether (x, y) L in time f(k) n , where f is an arbitrary function and is a constant. Definition does not change if f(k) n is replaced by f(k) + n (!)

Parametrized complexity - Definitions Mk for every n solves the problem in time f(k) n For each k there is a constant ck, such that f(k) n > n + 1 for n ck M'k: - simulates Mk for n ck - looks up value from the table for n ck M'k solves the problem in time fꞌ(k) ck + n a+1