Algorithms Design and Analysis 240 310 Semester 2

Algorithms: Design and Analysis 240 -310 , Semester 2, 2020 -2021 2. Backtracking • Objectives o explain backtracking search, and give three examples (all subsets, permutations, and 8 -queens) 240 -310 Algs: 3. Backtracking 1

1. Backtracking Features • Search down a data structure to the 'end' o e. g. search a binary tree • The search involves choices about which path to take o e. g. go to left or right child? o let's go left! • At 'end', go back to last choice point, and try a different choice. o e. g. go back to parent node, let's go right! • Stop when back at start, and no more choices. 240 -310 Algs: 3. Backtracking 2

1. 1. Backtracking Example Backtracking recursion inside a loop 240 -310 Algs: 3. Backtracking 3

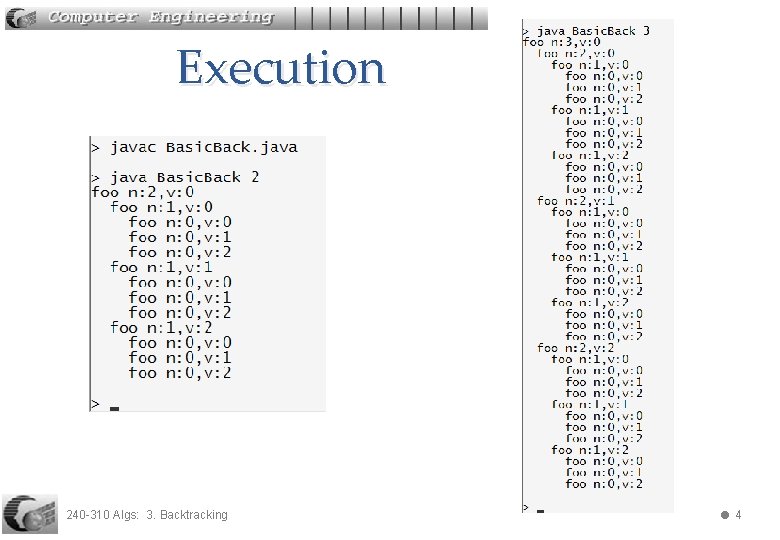
Execution 240 -310 Algs: 3. Backtracking 4

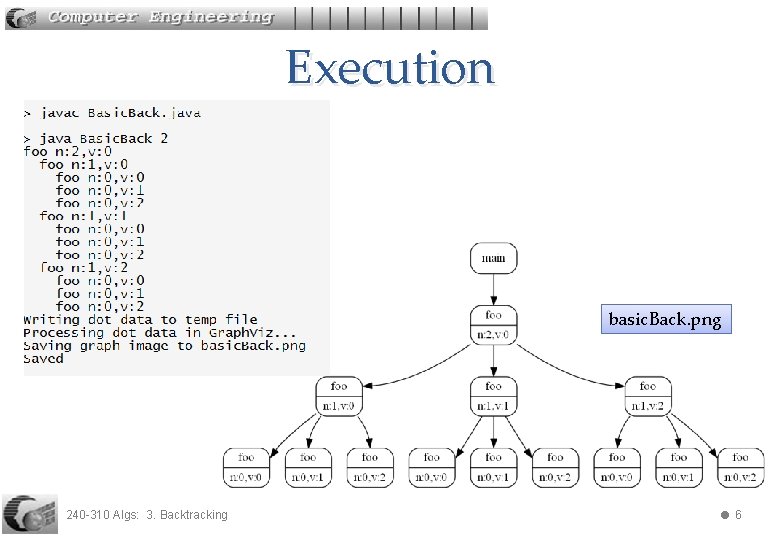
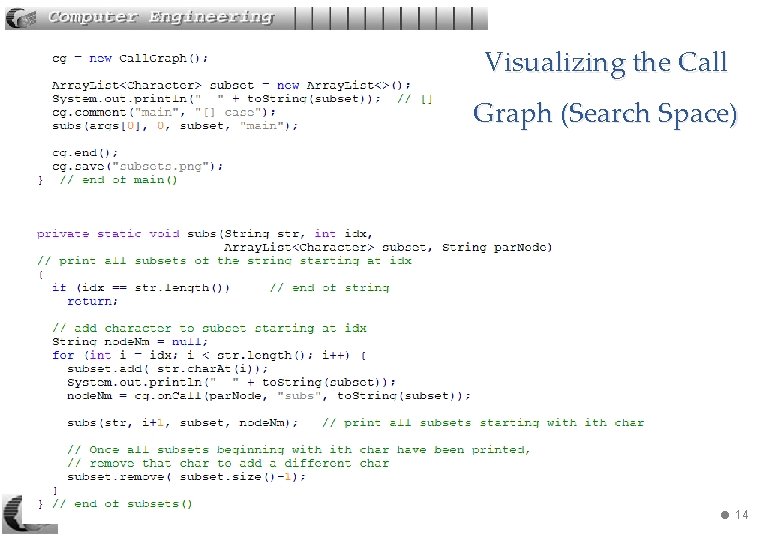
1. 2. Visualizing the Call Graph Include Call. Graph. java in the folder and add calls to it in Basic. Back. java to generate a call graph. 240 -310 Algs: 3. Backtracking 5

Execution basic. Back. png 240 -310 Algs: 3. Backtracking 6

Call. Graph uses Graph. Viz • If you want to use Call. Graph. java, download it from http: //fivedots. coe. psu. ac. th/~ad/callgraph • You also need to install Graph. Viz: https: //graphviz. gitlab. io/ 240 -310 Algs: 3. Backtracking 7

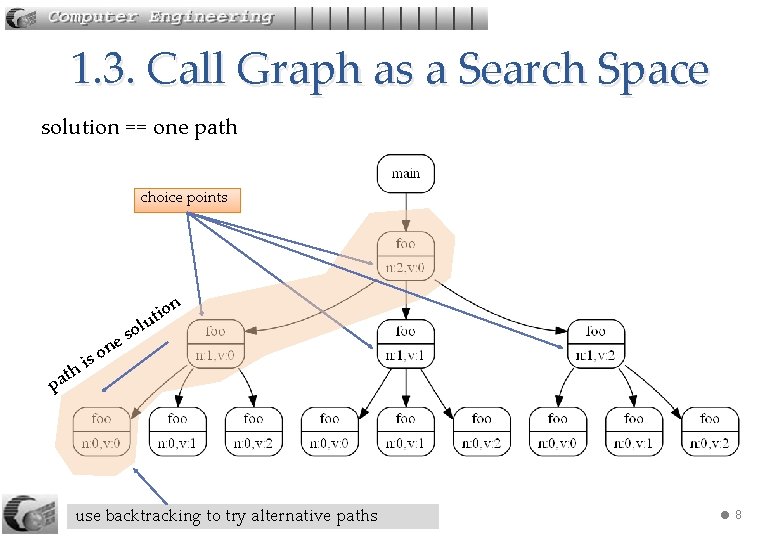
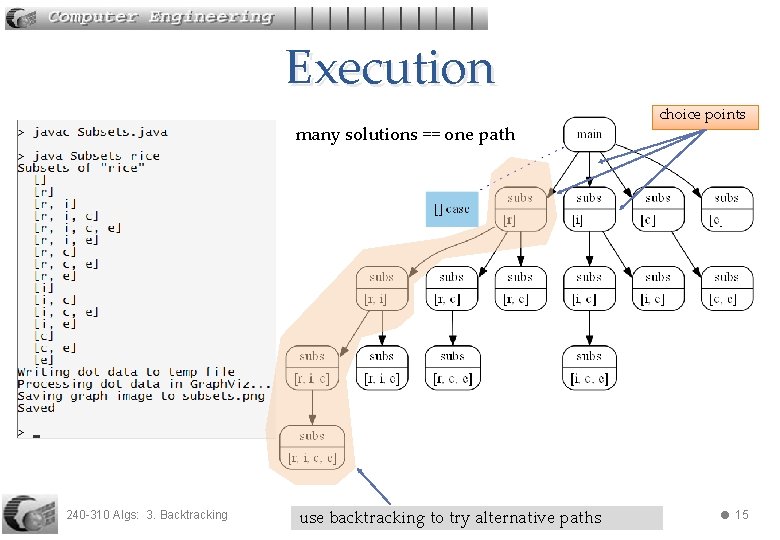
1. 3. Call Graph as a Search Space solution == one path choice points n p ath ne o s io t u ol s i 240 -310 Algs: 3. Backtracking use backtracking to try alternative paths 8

1. 4. What is a Search Space? • The problem may have many answers, spread across a very large “search space” • Brute force strategy: look at all the answers in the search space to find the best one(s) • Today’s CPUs can handle search spaces containing billions of answers (about 109) • In some problems, we can stop as soon as one answer is found – fast but answer may not be the best 240 -310 Algs: 3. Backtracking 9

Calculating the Search Space Size • Search space size is related to the number of variables in the problem, and their values o e. g. , 20 variables, each one 0 or 1; there are 220 different solutions, or about 106 o e. g. , 12 variables, each one 0, 1, 2, …, or 9; there are 1012 different solutions o e. g. , 12 variables, holding the permutation of 1, 2, 3, …, 12; there are 12! = 479, 001, 600 different solutions ≈ 5 x 108 240 -310 Algs: 3. Backtracking 10

2. Constructing All Subsets • Given a set with n items, we have 2 n subsets. How to output all the subsets? • E. g. , the subsets of {a, b, c } are {abc} {ab} {ac} {a} {bc} {b} {c} {} 240 -310 Algs: 3. Backtracking 11

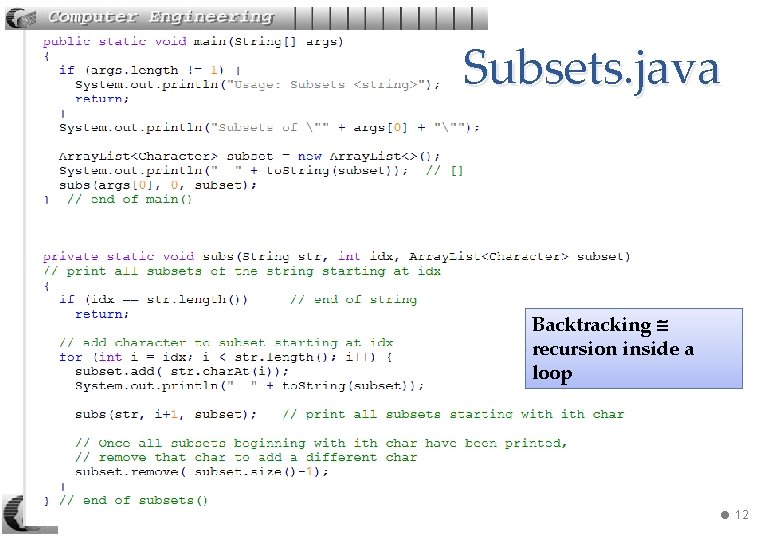
Subsets. java Backtracking recursion inside a loop 240 -310 Algs: 3. Backtracking 12

Execution • The program generates subsets of a supplied string, which it treats as a list of characters. 240 -310 Algs: 3. Backtracking 13

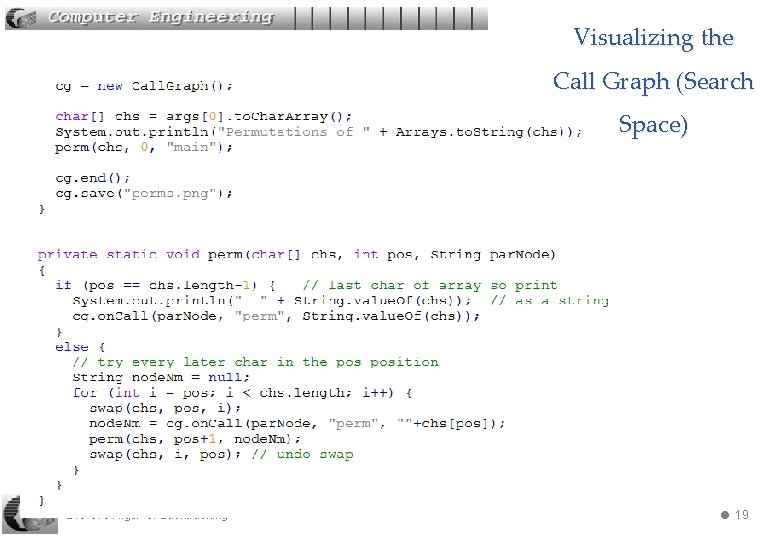
Visualizing the Call Graph (Search Space) 240 -310 Algs: 3. Backtracking 14

Execution many solutions == one path 240 -310 Algs: 3. Backtracking use backtracking to try alternative paths choice points 15

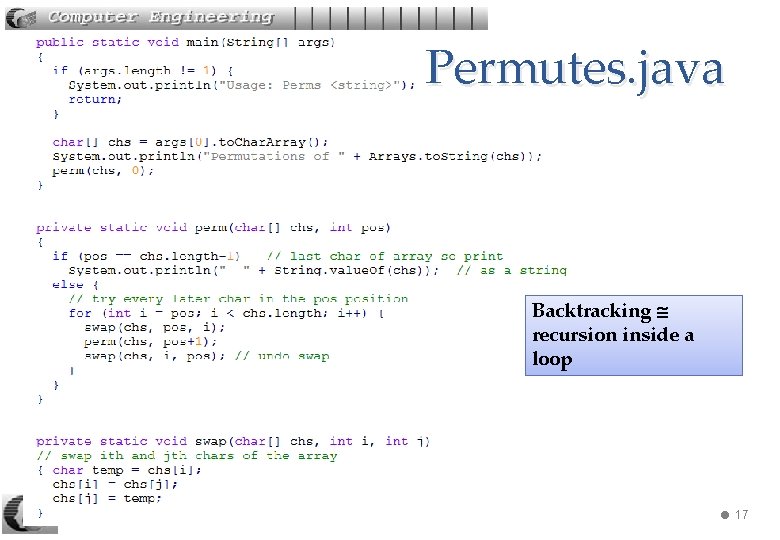
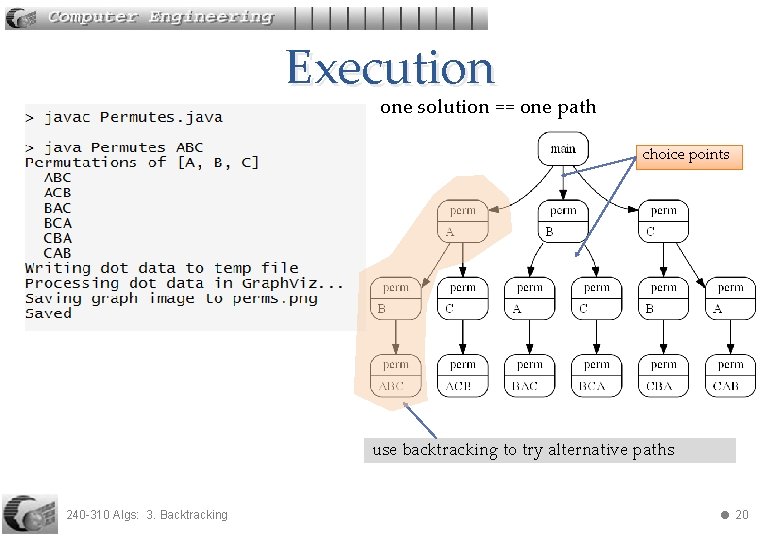
3. Constructing All Permutations • Permutation of "ABC" are ABC ACB BAC BCA CBA CAB 240 -310 Algs: 3. Backtracking The trick is to use backtracking and swapping 16

Permutes. java Backtracking recursion inside a loop 240 -310 Algs: 3. Backtracking 17

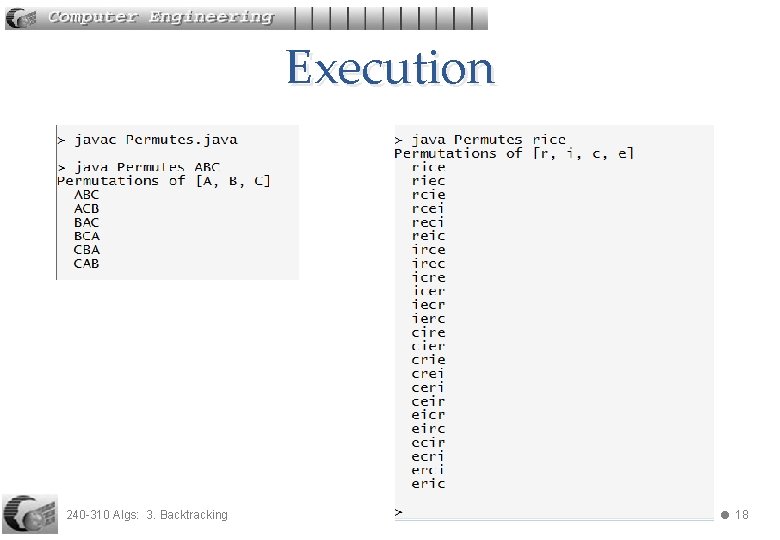
Execution 240 -310 Algs: 3. Backtracking 18

Visualizing the Call Graph (Search Space) 240 -310 Algs: 3. Backtracking 19

Execution one solution == one path choice points use backtracking to try alternative paths 240 -310 Algs: 3. Backtracking 20

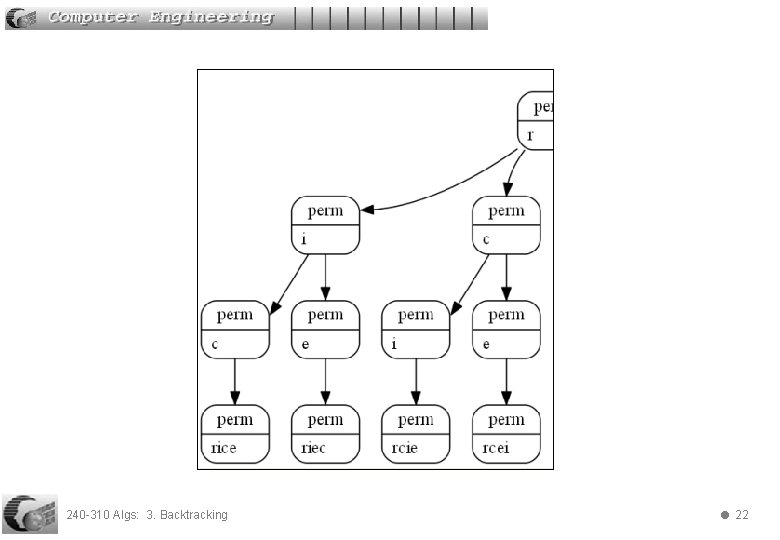
Search Space for "rice" 240 -310 Algs: 3. Backtracking 21

240 -310 Algs: 3. Backtracking 22

4. Eight-Queens Problem • Put 8 queens on an 8× 8 chessboard such that none of them is able to affect any of the others. • A solution requires that no two queens share the same row, column, or diagonal. • How many solutions? (92) 240 -310 Algs: 3. Backtracking 23

Eight-Queens Problem • If a queen can be placed at any square, the search space is 648. Maybe too large! (648 == 26*8 == 248 ≈ 1012 * 28 = 2. 56 x 1014) • Position constraints help to reduce the size of search space o The queen in the first column has 8 choices. o Next, the queen in the second column has 7 choices. o Next, the queen in the third column has 6 choices. Etc. • Using these constraints, the space size is 8! = 40320 only. • We can also add diagonal constraints to reduce the size more 240 -310 Algs: 3. Backtracking 24

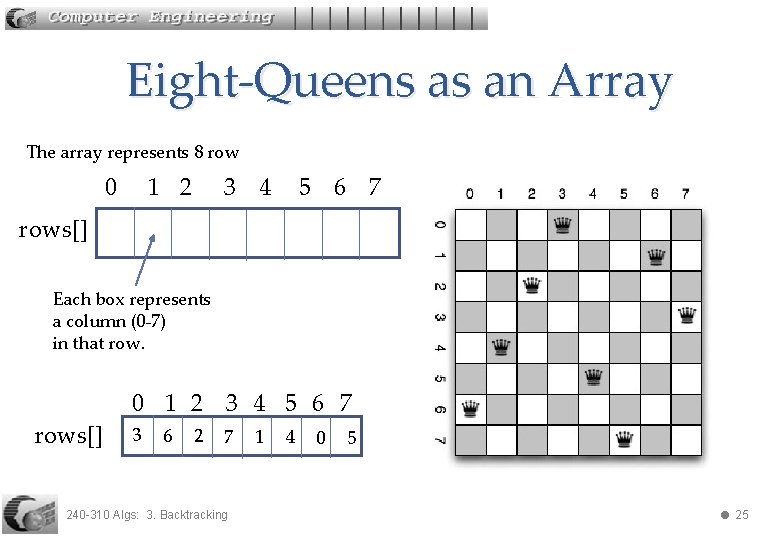
Eight-Queens as an Array The array represents 8 row 0 1 2 3 4 5 6 7 rows[] Each box represents a column (0 -7) in that rows[] 0 1 2 3 4 5 6 7 3 6 2 7 240 -310 Algs: 3. Backtracking 1 4 0 5 25

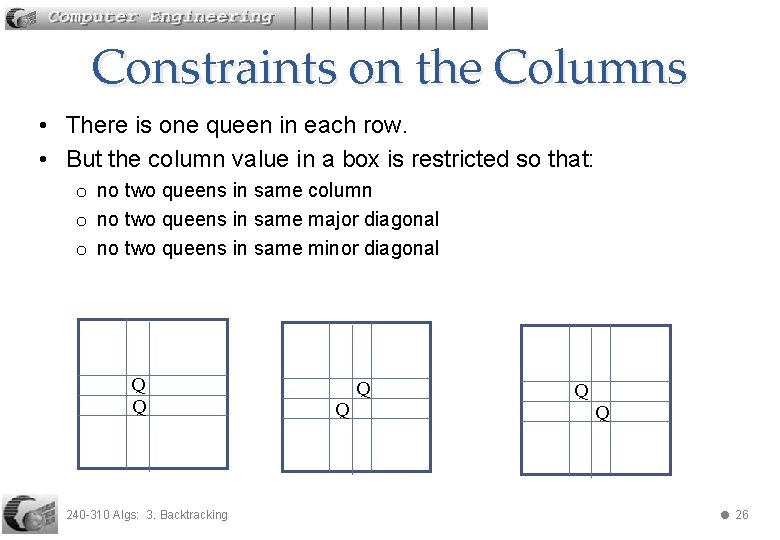
Constraints on the Columns • There is one queen in each row. • But the column value in a box is restricted so that: o no two queens in same column o no two queens in same major diagonal o no two queens in same minor diagonal Q Q 240 -310 Algs: 3. Backtracking Q Q 26

From Constraints to Numbers • Same Column • rows[i] == rows[k] e. g. rows[3] == rows[5] rows[] 0 1 2 3 4 5 6 7 5 5 i k 3 Q 5 240 -310 Algs: 3. Backtracking 27

• Same major diagonal • rows[i] – rows[k] == (k – i) • e. g. rows[3] - rows[5] == (5 – 3) rows[] 0 1 2 3 4 5 6 7 7 5 i k Q 3 5 Q 5 240 -310 Algs: 3. Backtracking 7 28

• Same minor diagonal • rows[k] – rows[i] == (k – i) • e. g. rows[5] - rows[3] == (5 – 3) rows[] 0 1 2 3 4 5 6 7 5 7 i k 3 Q 5 240 -310 Algs: 3. Backtracking 7 29

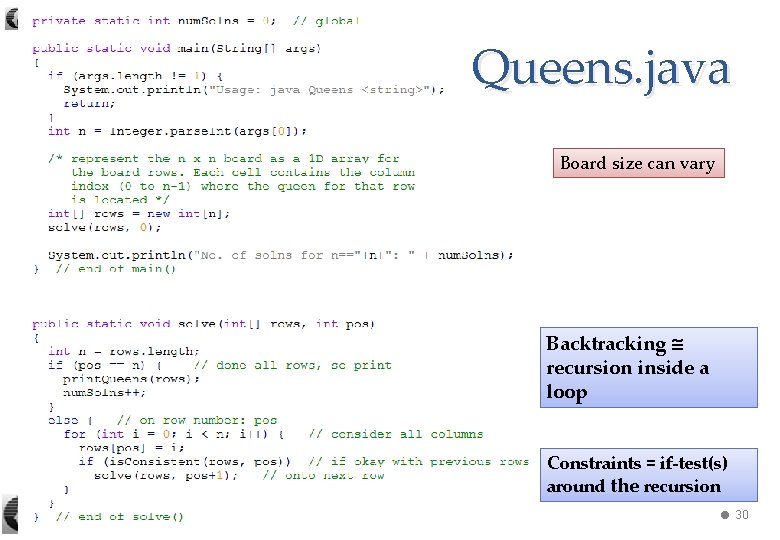
Queens. java Board size can vary Backtracking recursion inside a loop Constraints = if-test(s) around the recursion 240 -310 Algs: 3. Backtracking 30

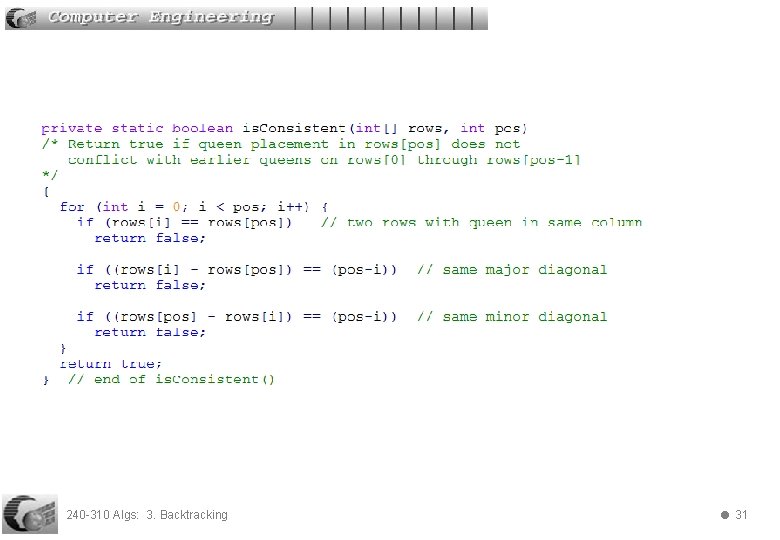
240 -310 Algs: 3. Backtracking 31

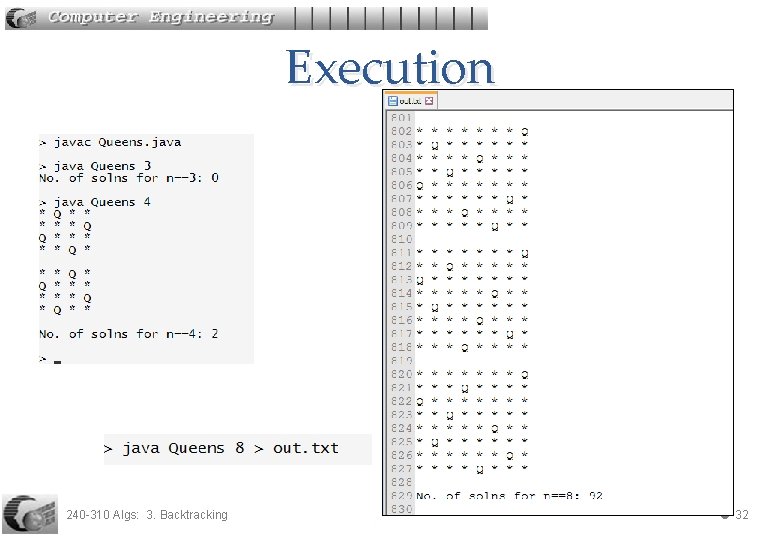
Execution 240 -310 Algs: 3. Backtracking 32

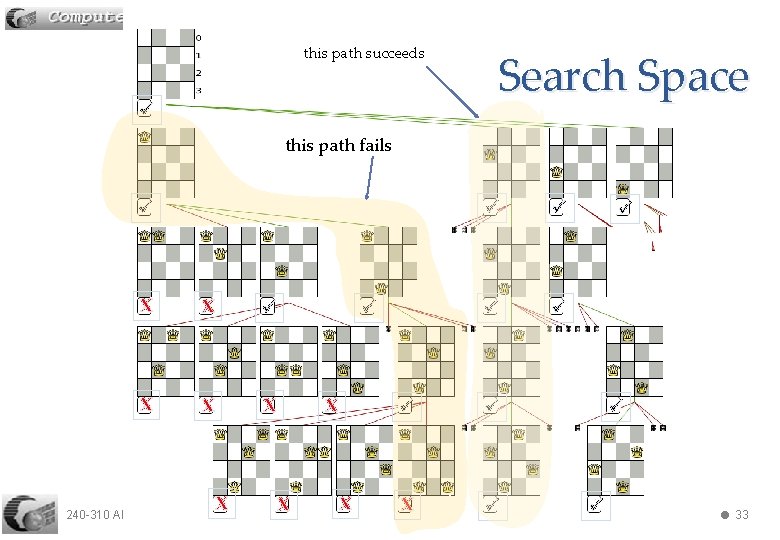
this path succeeds Search Space this path fails X X X 240 -310 Algs: 3. Backtracking X X X 33

Using Call. Graph 240 -310 Algs: 3. Backtracking 34

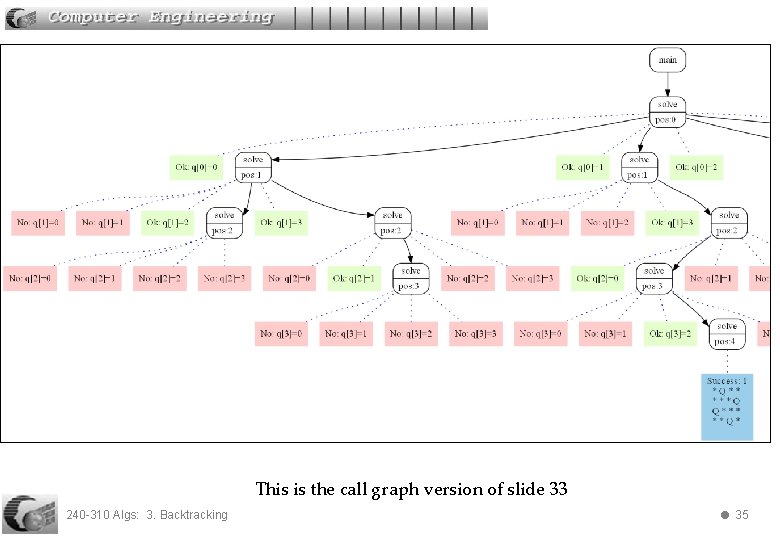
This is the call graph version of slide 33 240 -310 Algs: 3. Backtracking 35