Algorithms Course 1 Algorithms Efficiency Analysis and Order

演算法課程 (Algorithms) Course 1 演算法: 效率、分析與量級 Algorithms: Efficiency, Analysis, and Order

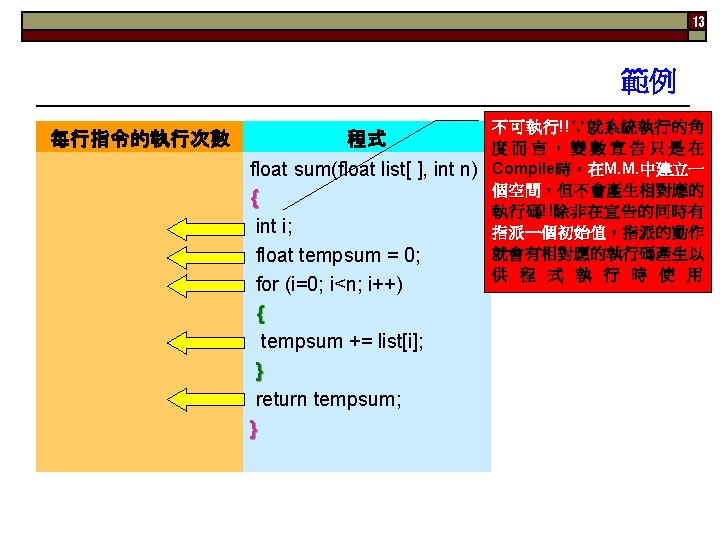
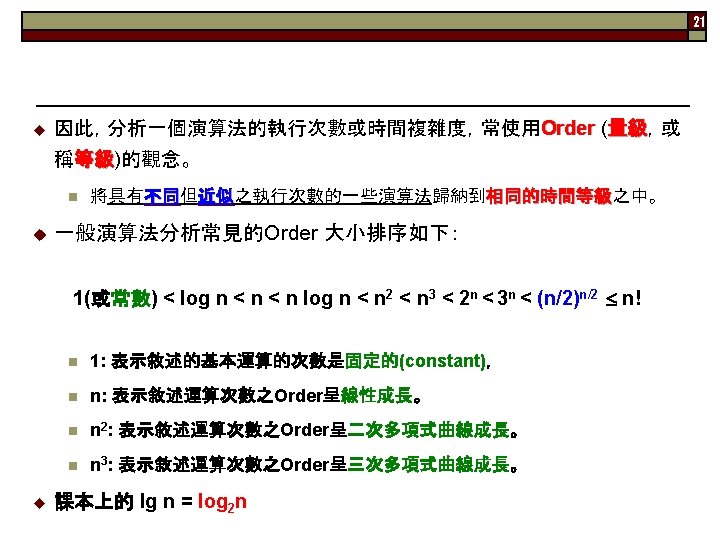
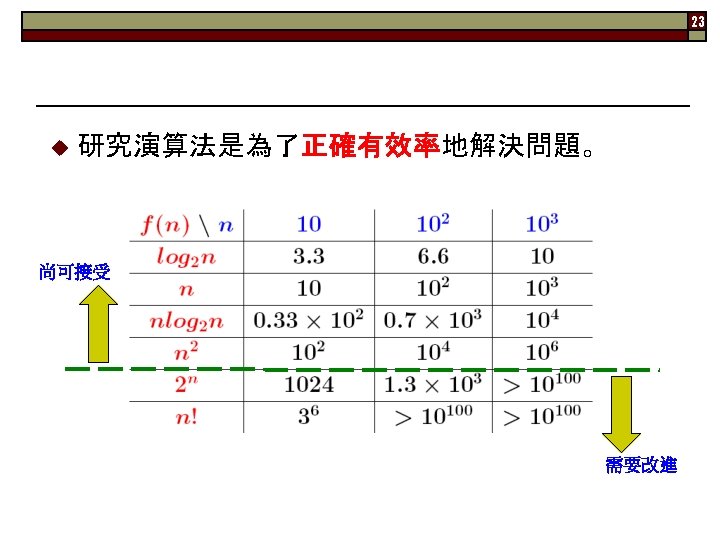
2 ▓ Outlines u 本章重點 n Algorithm ¡ ¡ n n The Importance of Developing Efficient Algorithms Analysis of Algorithms ¡ ¡ n Space complexity Time complexity Asymptotic Notation (漸近式表示) ¡ ¡ n Def. 與5個性質 Pseudocode Order , , , o, Using a Limit to Determine Order

5 Pseudocode (虛擬碼) Note: One of the most common tools for defining algorithms is pseudocode, which is part English, part Structured Code.

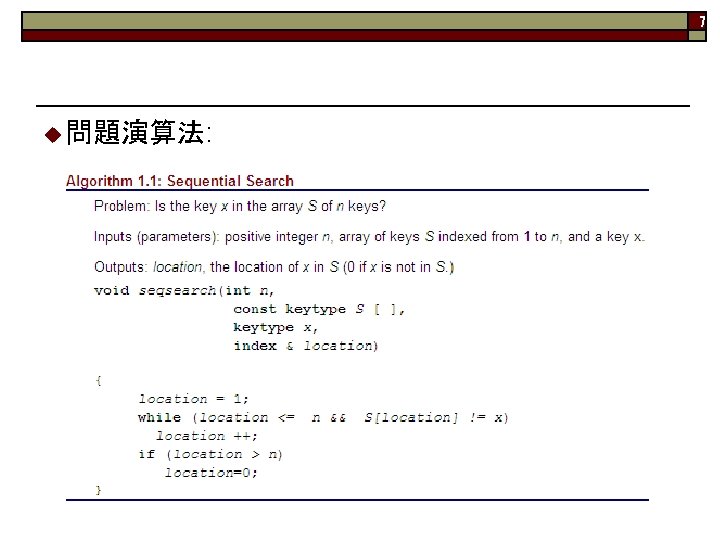
6 Example of Pseudocode u 問題1: 搜尋問題 u 範例:

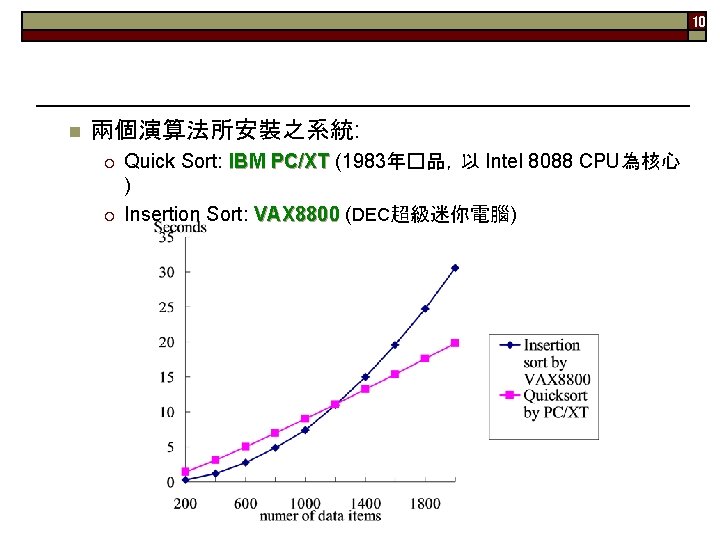
10 n 兩個演算法所安裝之系統: ¡ ¡ Quick Sort: IBM PC/XT (1983年�品，以 Intel 8088 CPU為核心 PC/XT ) Insertion Sort: VAX 8800 (DEC超級迷你電腦)

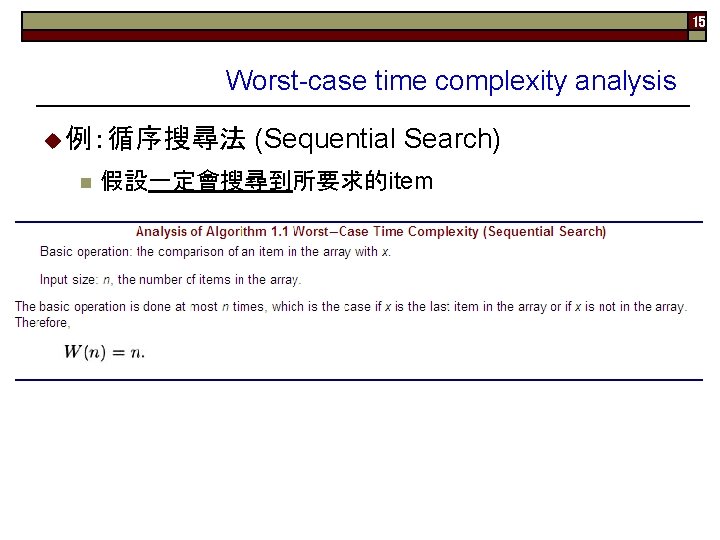
15 Worst-case time complexity analysis u 例：循序搜尋法 (Sequential Search) n 假設一定會搜尋到所要求的item

16 Best-case time complexity analysis u 假設一定會搜尋到所要求的item

17 Average-case time complexity analysis u 假設一定會搜尋到所要求的item

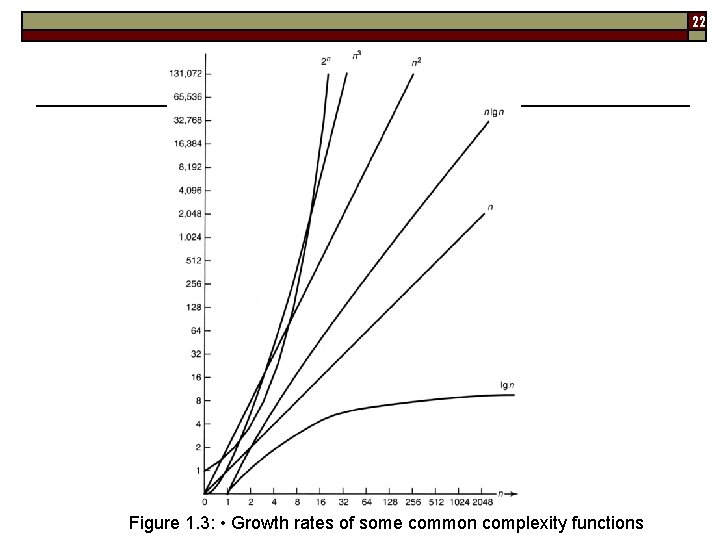
22 Figure 1. 3: • Growth rates of some common complexity functions

25 以嚴謹的方式介紹Order u 共有五種漸近式表示方法： Big-O (O) n Omega ( ) n Theta ( ) n Small-O (o) n Small-Omega ( ) n

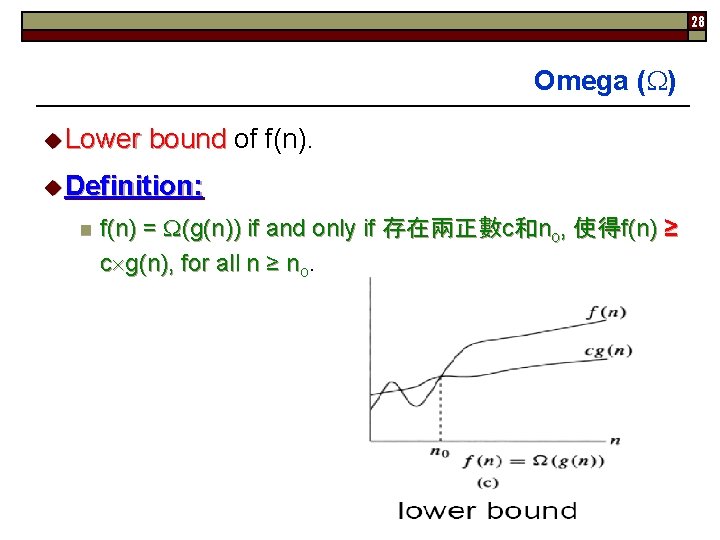
28 Omega ( ) u Lower bound of f(n). Lower bound u Definition: n f(n) = (g(n)) if and only if 存在兩正數c和no, 使得f(n) ≥ c g(n), for all n ≥ no.

30 Theta ( ) u 較 O 與 精確. u Definition: f(n) = (g(n)) if and only if 存在三正數c 1, c 2和no, 使得 c 1 g(n) ≤ f(n) ≤ c 2 g(n), for all n ≥ no. n

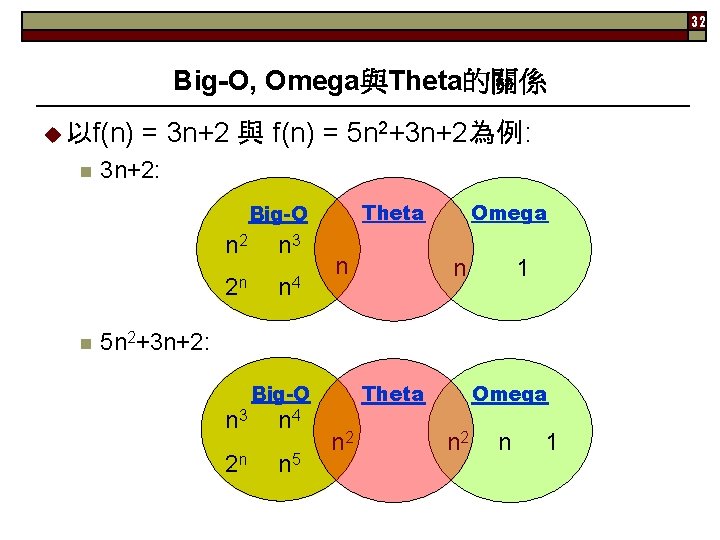
32 Big-O, Omega與Theta的關係 u 以f(n) = 3 n+2 與 f(n) = 5 n 2+3 n+2為例: n 3 n+2: n n 2 n 3 2 n n 4 Omega Theta Big-O n n 1 5 n 2+3 n+2: n 3 2 n Big-O n 4 n 5 Theta n 2 Omega n 2 n 1

33 Small-O (o) u Definition: n f(n) = o(g(n)) if and only if 對任何正數c，會存在一個正 數no, 使得f(n) < c g(n), for all n ≥ no. u 與Big-O的比較: n n f(n) = O(g(n)) if and only if 存在兩正數c和no, 使得f(n) ≤ c g(n), for all n ≥ no. 例如: ¡ ¡ 2 n = o(n 2) 2 n 2 ≠ o(n 2)，但是 2 n 2 = O(n 2)。

34 Small-Omega ( ) u Definition: n f(n) = (g(n)) if and only if對任何正數c，會存在一個正 數no, 使得f(n) > c g(n), for all n ≥ no. u 與Omega的比較: n n f(n) = (g(n)) if and only if 存在兩正數c和no, 使得f(n) ≥ c g(n), for all n ≥ no. 例如: ¡ ¡ 5 n 2+3 n+2 = (n) 5 n 2+3 n+2 ≠ (n 2)，但是 5 n 2+3 n+2 = (n 2)

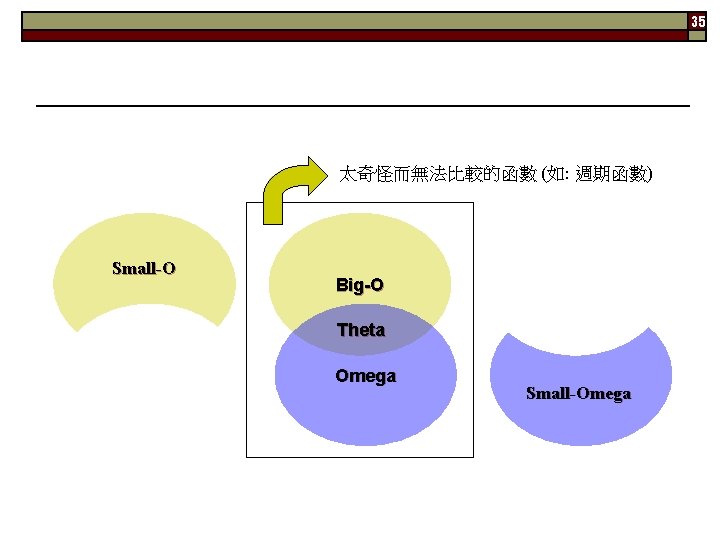
35 太奇怪而無法比較的函數 (如: 週期函數) Small-O Big-O Theta Omega Small-Omega

37 u 邏必達法則 (L’ Hospital Rule)

38 Ex: Determine if f(n) = O 1. f(n) = log 54 n, g(n) = log 45 n Sol: (g(n)) or neither

39 2. f(n) = 1. 10. 1 n, g(n) = n 3 Sol:

40 3. f(n) = n cot(n), g(n) = n tan(n) Sol:

42 � 課後練習� u 課文內容: n Example 1. 7, Example 1. 9, Example 1. 10, Example 1. 11 Example 1. 12, Example 1. 13, Example 1. 15, Example 1. 17, Example 1. 18, Example 1. 19, Example 1. 24, Example 1. 25, Example 1. 26, Example 1. 27, Example 1. 28. u 習題: n n 15, 16, 17, 18 (上學期資結Ch. 1有教), 24 21 請自行參考洪捷p. 1 -10定理3及例題7~10 u 洪捷演算法Ch. 1: n n 例 1~6 精選範例 1, 2

45 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩ log n = log (log n) logkn = (log n)k a = blogba logcab = logca+ logcb Logca/b = logca- logcb logban = n logba = logca/ logcb logba = 1/ logab logb(1/a) = logba-1 = -logba a logbc= c logba

48 補 3: 補充考題 u Ex 1: Show the following equality is incorrect (91交大) n 2/log n = (n 2) Sol 1: (以極限來做)