Algorithms complexity Parallel computing Yair Toaff Gil Ben

Algorithms complexity Parallel computing Yair Toaff Gil Ben Artzi Orly Margalit 027481498 025010679 037616638

Parallel computing - MST The problem: Given a graph G= (V , E) with weights. We need to find a minimal spanning tree with the minimum total weight.

Parallel computing - MST Kruskal algorithm • Sort the graphs edges by weight. • In each step add the edge with the minimal weight that doesn’t close a cycle.

Parallel computing - MST Complexity Single processor: Sorting – O(m log m) = O( n 2 log n) For each step O(1) there are O(n 2) steps Total – O(n 2 log n )

Parallel computing - MST O(m) processors: Sorting O( log 2 m ) Each step O(1) Total O( n 2 )

Parallel computing - MST Prim algorithm • Randomly choose a vertex for tree initialization. • In every step choose the edge with minimal weight form a vertex in the tree to a vertex not in the tree.

Parallel computing - MST Complexity Single processor: Find the edge in step i O( n * i) Total n + 2 n + … + n 2 = O(n 3)

Parallel computing - MST O(n) processors: There is a processor for each vertex so every step takes O(n) Total O(n 2)

Parallel computing - MST O(m) processors In each step there are more processors then edges so finding the minimum takes O( log n) Total O ( n log n)

Parallel computing - MST O(m 2) processors In each step finding the minimum takes O( 1) Total O ( n)

Parallel computing - MST Sulin algorithm • Treat every vertex as a tree • In each step randomly choose a tree and find the edge with the minimal weight from a vertex in the tree to a vertex not in the tree

Parallel computing - MST Complexity: Single processor Same as Kruskal algorithm

Parallel computing - MST O(n) processors: There is a processor for every vertex so finding the minimum takes O( n ) In each step only half of the trees remain so there are O ( log n ) steps Total O( n log n)

Parallel computing - MST O( n 2 ) processors: There are n processors for every vertex so finding the minimum takes O(log n) Total O(log 2 n )

Parallel computing - MST O( n 3 ) processors: There are n 2 processors for every vertex so finding the minimum takes O(1) Total O(log n )

Merge Sort MS( p, q, c) - p, q indexes c is the array If ( p < q ) { MS( p , (p+q)/2 , c ) MS( (p+q)/2 , q , c ) merge( p , (p+q)/2 , q , c) }

Merge Sort Single processor In every step the merge takes O(n), there are O(log n) steps. Total O( n log n )

Merge Sort O(n) processors: In every step the merge is done in parallel time( MS(n)) = O(1) + time(merge( n / 2)) By using regular merge we get O( 1 + 2 + 4 + … + n ) = (2 log n + 1) = O(n)

Merge Sort Parallel merge The problem: given 2 sorted arrays A, B with size n/2 we need to merge them efficiently while keeping them sorted

Merge Sort Let us define 2 sub arrays: ODD A = [a 1 , a 3 , a 5 …] EVEN A = [a 0 , a 2 , a 4 …]

Merge Sort And 2 functions: Combine( A , B ) = [ a 0 , b 0 , a 1 , b 1 , … ] Sort-combined( A ) – for each pair a 2 i a(2 i+1) if they are in the right order do nothing else replace each of them with the other

Merge Sort Parallel merge ( A , B ) { C = parallel merge ( ODD A , EVEN B ) D = parallel merge ( ODD B , EVEN A ) L = combine ( C , D ) Return (sort-combined ( L ) ) }

Merge Sort Complexity: Time ( parallel merge ( n ) ) = Time ( parallel merge ( n/2) ) + O(1) = O(log n)

Merge Sort What is left is to prove the algorithm. Theorem: if an algorithm sort every array of (0 , 1) it will sort every array.

Merge Sort Let us mark the number of ‘ 1’ in A as 1 a and in B as 1 b The number of ‘ 1’ in ODD A is 1 a /2 The number of ‘ 1’ in EVEN A is 1 a /2

Merge Sort As a result of it the difference between the number of ‘ 1’ in C and in D is 0 or 1. Array L will be sorted except maybe one point where the ‘ 0’ and ‘ 1’ meet sort-combined will do 1 swap at most.

Merge Sort Complexity of merge sort using parallel merge: Log 1 + log 2 + log 4 + log 8 + … + log n = 0 + 1+ 2 + 3 + … + log n = O( log 2 n)

Sum • • Input : Array of n elements of type integer. Output : Sum of elements. One processor - O(n) operations. Two processors - Still O(n) operations.

Sum • What could we do if we have O(n) processors ? • Parallel algorithm – For each phase till we have only one element • Each processor adds two elements together • We have now N/2 new elements • Complexity – We have done more operations , so what have we gained ? – Since in each phase we stay with only half of the elements, we can view it as a binary tree where each level represents the new current elements, overall depth is O(logn) levels. Each level in the tree is O(1), total of O(logn) time.

Max 1 – Max 2 • Input : Array of n elements of type integer. • Output : The first and the second maximum elements in the array • One processor , 2 n operations. • Two processors , each insertion takes 3 operation (compare to each of the other elements that are candidates ) , 2 n/3 operations

Max 1 – Max 2 • Parallel algorithm - recursive solution – Divide 2 groups (G 1, G 2). – Find MAX for each group (Local. M 1, Local. M 2) – If Local. M 1>Local. M 2 • Create new group G 3 : = (Local. M 2+G 1) • MAX 2 must be in G 3, since in G 2 there is no element that is bigger than Local. M 2

Max 1 – Max 2 • Example – End of recursive M 1[10] * M 1[7] * M 1[1] * M 1[3] * M 1[100] * M 1[8] * M 1[55] * M 1[6] – Up one phase M 1[10], M 2[7] * M 1[3], M 2[1] * M 1[100], M 2[8] * M 1[55], M 2[6] – Up one phase M 1[10], M 2[7, 3] * M 1[100], M 2[8, 55] – The result M 1[100] * M 2 [10, 8, 55]

Max 1 – Max 2 • Complexity – 1 processor • n operations of comparing all elements in tree for Max 1 , logn operation comparing elements for Max 2, Total (n+logn) – O(n) processors • We could find Max 1 and rerun the algorithm to find Max 2, each in logn, total of 2 logn. • However , we can use the previous algorithm and add G 3 in parallel , and we get logn for finding Max 1, loglogn for finding Max 2

Max & Min groups • Input : 2 groups ( G 1, G 2) of sorted elements • Output : 2 groups (G 1`, G 2`), where in one group all elements are bigger than all the elements in the other group • One processor - Insert all elements into 2 stack, always compare the stack heads, the minimum is inserted into the Min group. • Complexity - O(n) operations

Max & Min groups • There is a major subtle in the previous algorithm when trying to apply it to parallel computing – each element must be compared until we will find an element that is higher himself. • We would like to find a method to compare as less as we can each elements with the others , the best is only one comparison per element. • Any member of the min group is necessarily smaller than at least half of the elements. • If we could conclude this, we can classified the element in the right group immediately • Any suggestion ?

Max & Min groups • Parallel algorithm – Insert all elements from G 1 into list L 1 in a reverse order , and all elements of G 2 into list L 2 in regular order – Element j in L 1 is bigger than n-j-1 elements of his list – Element j in L 2 is bigger than j-1 elements of his list – So , by comparing element i in both lists we get • If L 1[i]>L 2[i] , L 1[i] is bigger than n-i-1 elements in L 1 , and i+1(including L 2[i]) elements in L 2 , total of n elements. L 2[i] is smaller than n-i elements of L 2 and i+1 elements element of L 1 , total of n elements. • And vice versa – We can now insert the element immediately to their groups

Max & Min groups • Example – Groups • G 1 = 7, 100, 101 • G 2 = 1, 18, 99 – Lists • L 1 = 101, 100, 10, 7 • L 2 = 1, 18, 99 – Comparing : (101, 1), (100, 11), (10, 18), (7, 99) – Result : G 1’= 101, 100, 18, 99 , G 2’ = 1, 10, 7

Max & Min groups • Complexity – We have compare element i of each lists – Each element has only one comparison – O(n) processor , O(1) time ! – Can we do better for one processor now ?

Signed elements • Input : Array of elements , some of them are signed • Output : 2 Arrays of elements , one contain the signed , the other the unsigned, keeping the order between the elements • One processor – Make one pass , drop each element into the correct array – O(n) operations • Since we need to maintain the order between the elements , we must know for each element , how many elements should be before him • how could we improve the Algorithm by adding more processors ?

Signed elements array • Parallel algorithm – Create another array (A 2) of elements, where in each location of a signed element insert 1 and in each location of unsigned elements insert 0 – Now we can do the parallel prefix algorithm and obtaining each element position in the destination array – We can do the same for the unsigned elements

Signed elements array • Example – Input : [x 1, x 2, x 3`, x 4, x 5`, x 6, x 7`, x 8`, x 9] – A 2 : [0 , 1 , 0 ] – Prefix: [0 , 1 , 2 , 3 , 4 ] – Result: x 3’ 1 , x 5` 2 , x 7` 3 , x 8` 4 • Complexity – O(n) processor , O(logn) time !

Scheduling • Input : Array of jobs , contains the time for executing each job , and the deadline for finishing it. • Output : Is there a scheduling satisfying the above condition ? • Parallel algorithm – Sort the deadlines – Create prefix for executing time of each job – In order to exist a scheduling , Prefix. Exec. Time(i)<Dead. Line[i] • Complexity O(n) processors – O(logn) to sort, O(logn) to do prefix , O(1) to compare

CAG - Clique • Input : CAG • Output : maximum clique exist • Reminder – Clique : A vertex is in a clique iff there is an edge from each of the vertex in the clique to himself – CAG : Circular Arc Graph , A graph where each vertex is on a circle. There is an edge between two vertex iff there is a join segment on the circle between those two vertex

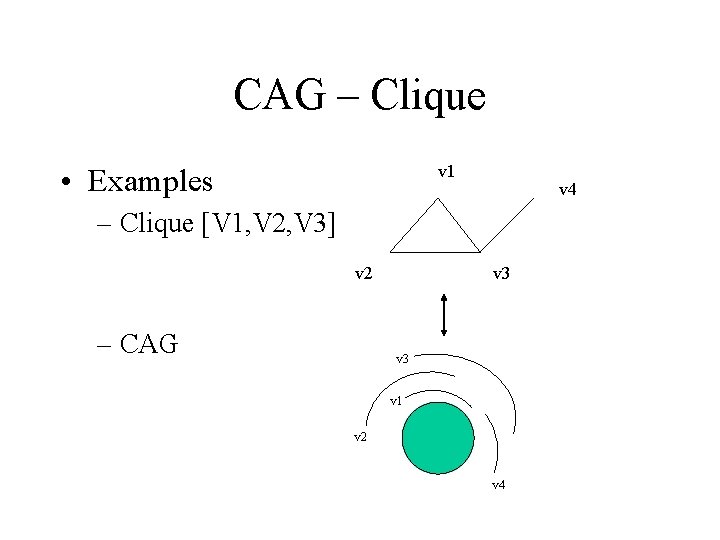
CAG – Clique v 1 • Examples v 4 – Clique [V 1, V 2, V 3] v 2 – CAG v 3 v 1 v 2 v 4

CAG - Clique • Parallel algorithm – Loop through element list twice • If Element == start of a vertex , Boundries. Array[i]=+1; • If Element == end of a vertex , and we already pass the start of this vertex , Boundries. Array[i]= -1 ; – Prefix. Array : = Prefix ( Boundries. Array) – Max. Clique : = Max ( Prefix. Array)

CAG - Clique • Example , CAG from previous slide – Boundries. Array [ (v 1, +), (v 2, +), (v 1, -), (v 4, +), (v 3, -), (v 4, -), (v 2, +), (v 1, + ), (v 3, + )(v 2, -), (v 1, -)] – Prefix. Array [1, 2, 1, 0, 1, 2, 3, 2, 1] – Max. Clique is 3 ! • Note : There is a need to loop twice trough the list of vertex since we consider only end of vertex that we already pass the start.

CAG – Clique • Complexity – One processor , O(n) – O(n) processors , logn + logn – O( n^2) processors , logn + o(1)

Exclusive Read & Exclusive Write • EREW • Most simple computer • Only one processor can read/write to a certain memory block at a time

Concurrent Read & Exclusive Write • CREW • Only one processor can write to a certain memory block at a time. • Multiple processors can simultaneously read from a common memory block.

Exclusive Read & Concurrent Write • ERCW • Only one processor can read a certain memory block at a time. • Multiple processors can simultaneously write to a common memory block.

Concurrent Read & Concurrent Write • • CRCW Most powerful computer Very complex memory control Multiple processors can simultaneously read/write to a common memory block

Concurrent Write Problem: • Multiple processors writing different values to a common memory block every processor overwrites on previous processor’s value.

Concurrent Write Solution 1: • Restrict Write – a unique value can only be written to the memory block.

Concurrent Write Solution 2: • Combine Write – a unique value is stored for every distinct processor in the shared memory block.

Restrict Write A good example of Restrict Write is a Boolean problem.

Restrict Write X 1 X 2 X 3 Result Initial value: Result = 0 Only value one is written to Result result = 0; For i = 1 to n doip (do in parallel) if (Xi = = 1) then result = 1; } {

Max Value - O(n 2) Processors Reminder: One processor : O(n) operations. O(n) processors : O(log 2 n) operations. O(n 2) processors : ? We can represent the comparison between numbers as a matrix. If x 1< x 2 then coordinate (1, 2) gets a value of one, else it gets a value of zero.

Max Value - O(n 2) Processors • A processor is allocated for each cell in the matrix. • All the processors with “value = 1” write simultaneously to the result cell in their row.

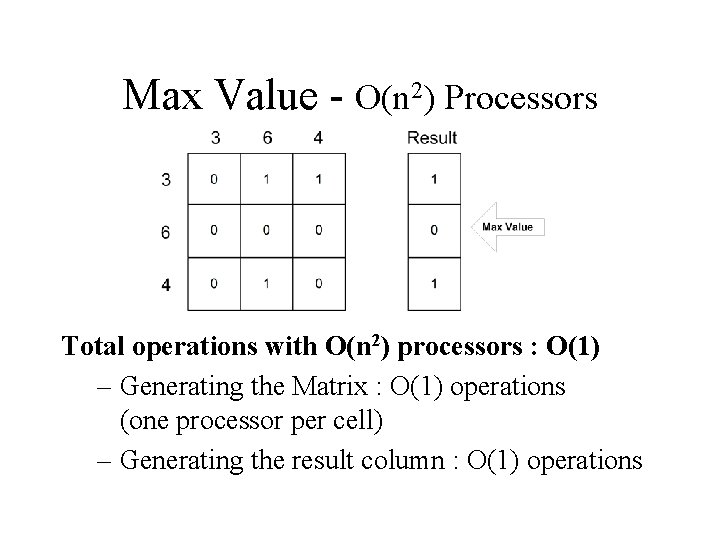
Max Value - O(n 2) Processors Total operations with O(n 2) processors : O(1) – Generating the Matrix : O(1) operations (one processor per cell) – Generating the result column : O(1) operations

Sort - O(n 2) Processors Reminder: One processor : O(nlog 2 n) operations. O(n) processors : O(log 22 n) operations (merge sort) O(n 2) processors : ? • As before, we generate a comparison matrix. • The result cells will receive the sum of the current row. Each row has O(n) processors, therefore the sum operation takes O(log 2 n) operations. • The result column represents the index of the sorted array in descending order.

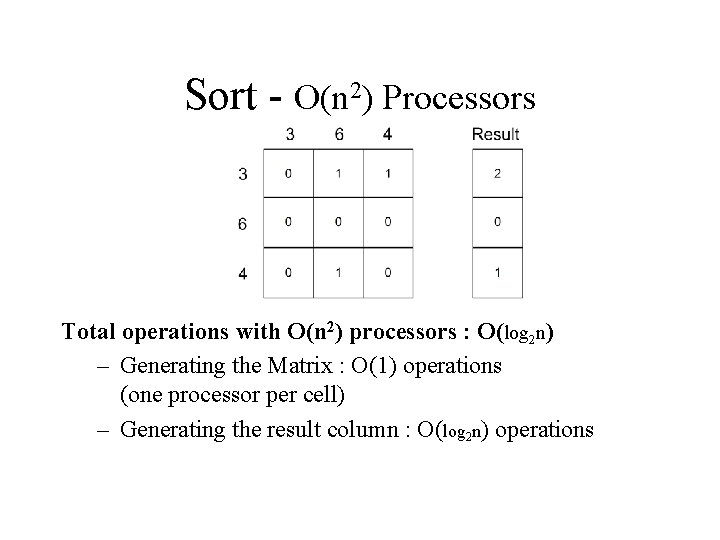
Sort - O(n 2) Processors Total operations with O(n 2) processors : O(log 2 n) – Generating the Matrix : O(1) operations (one processor per cell) – Generating the result column : O(log 2 n) operations

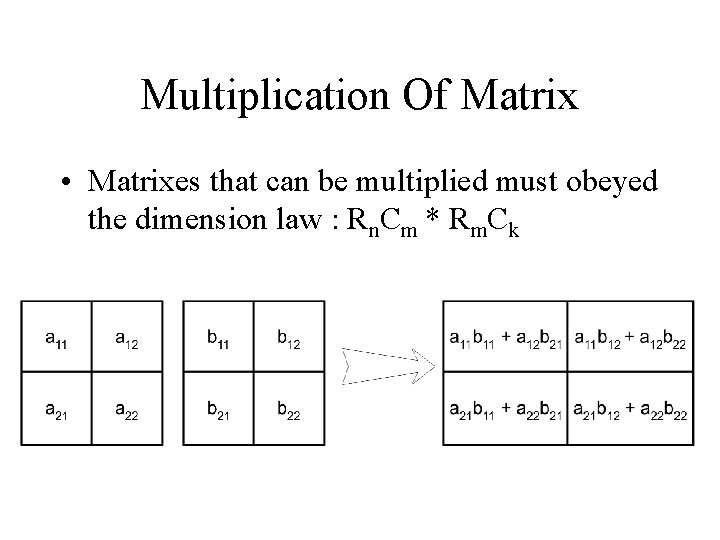
Multiplication Of Matrix • Matrixes that can be multiplied must obeyed the dimension law : Rn. Cm * Rm. Ck

Multiplication Of Matrix Input: Two matrixes of size n*n (Mnn) Output: One matrix Mnn Total operations with one processor : O(n 3) • n 2 cells • Sum of each cell with O(n) variables and one processor, O(n) operations

Multiplication Of Matrix Total operations with o(n) processors : O(n 2) • Processor per cell in a column. • n columns • Sum of each cell with O(n) variables and one processor, O(n) operations O(n)sum * ncolumn = O(n 2)

Multiplication Of Matrix Total operations with O(n 2) processors : O(n) • n 2 cells • Processor per cell • Sum of each cell with O(n) variables and one processor, O(n) operations O(n)sum * 1 cell = O(n) Each cell is summed simultaneously

Multiplication Of Matrix Total operations with O(n 3) processors : O(log 2 n) • n 2 cells • O(n) processors per cell • Sum of each cell with O(n) variables and O(n) processor, O(log 2 n) operations O(log 2 n)sum * 1 cell = O(log 2 n) Each cell is summed simultaneously

Multiplication Of Boolean Matrix Total operations with O(n 3) processors : O(1) • n 2 cells • O(n) processors per cell • Sum of each cell with O(n) variables and O(n) processor, O(1) operations O(1)sum * 1 cell = O(1) Each cell is summed simultaneously

Shortest Path Between Vertexes Problem: • Finding if path exists between 2 vertexes • Finding the shortest path between 2 vertexes

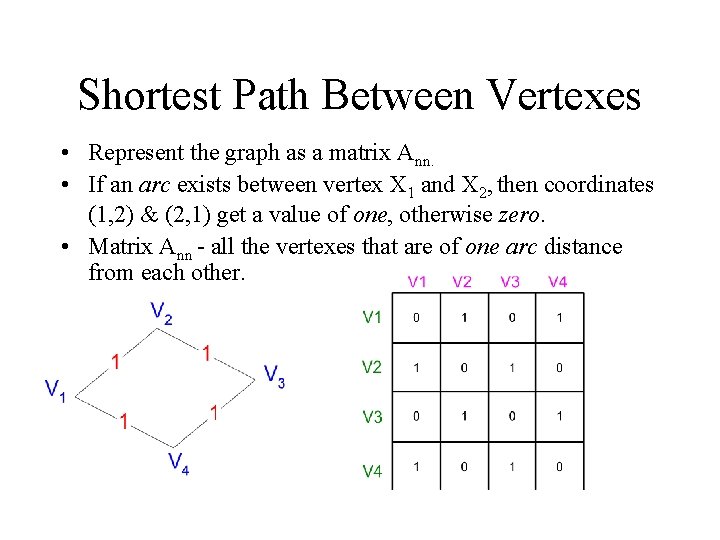
Shortest Path Between Vertexes • Represent the graph as a matrix Ann. • If an arc exists between vertex X 1 and X 2, then coordinates (1, 2) & (2, 1) get a value of one, otherwise zero. • Matrix Ann - all the vertexes that are of one arc distance from each other.

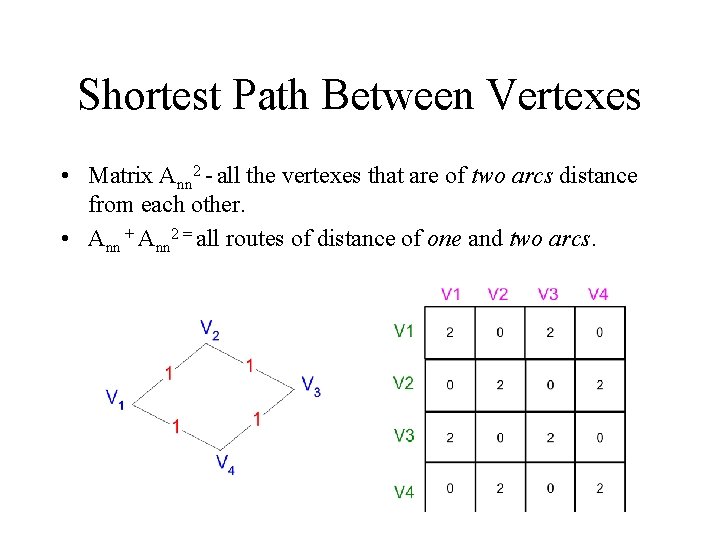
Shortest Path Between Vertexes • Matrix Ann 2 - all the vertexes that are of two arcs distance from each other. • Ann + Ann 2 = all routes of distance of one and two arcs.

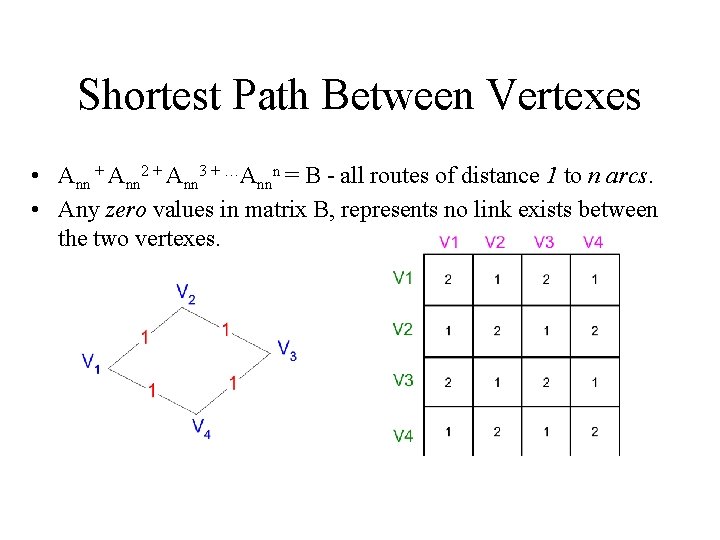
Shortest Path Between Vertexes • Ann + Ann 2 + Ann 3 + …Annn = B - all routes of distance 1 to n arcs. • Any zero values in matrix B, represents no link exists between the two vertexes.

Shortest Path Between Vertexes Total operations with 1 processors : O(n 4) • Building of Matrix Ann : O(n) operations • Multiplication of matrix : O(n 3) operations • Creation of Ann, Ann 2 , Ann 3 , … , Annn : O(n 4) operations • Sum of the Matrixes : O(n 3) operations

Shortest Path Between Vertexes Total operations with O(n) processors : O(n 3) • • Building of Matrix Ann : O(1) operations Multiplication of matrix : O(n 2) operations Creation of Ann, Ann 2 , Ann 3 , … , Annn : O(n 3) operations Sum of the Matrixes : O(n 2) operations (ncell * ncolumn)

Shortest Path Between Vertexes Total operations with O(n 2) processors: O(n 2) • Building of Matrix Ann : O(1) operations • Multiplication of matrix : O(n) operations • Creation of Ann, Ann 2 , Ann 3 , … , Annn : O(n 2) operations • Sum of the Matrixes : O(n) operations (process per cell)

Shortest Path Between Vertexes Total operations with O(n 3) processors: O(nlog 2 n) • Building of Matrix Ann : O(1) operations • Multiplication of matrix : O(log 2 n) operations • Creation of Ann, Ann 2 , Ann 3 , … , Annn : O(nlog 2 n) operations • Sum of the Matrixes : O(log 2 n) operations (o(n) processors per cell)

Shortest Path Between Vertexes Total operations with O(n 4) processors : O(log 22 n) • Building of Matrix Ann : O(1) operations • Multiplication of matrix : O(log 2 n) operations with O(n 3) processors • Creation of Ann, Ann 2 , Ann 3 , … , Annn : O(log 22 n) operations (prefix algorithm) • Sum of the Matrixes : O(log 2 n) operations • Boolean Output (link exist True or False) : O(log 2 n) operations