Algorithms and Networks 20162017 Johan M M van

Algorithms and Networks 2016/2017 Johan M. M. van Rooij Hans L. Bodlaender 1

Teacher 1: Johan van Rooij g Teacher (only on Tuesday) g Software Project. g Algorithms and Networks. g Master’s thesis projects. g Consultant / Data Scientist (rest of the week) g CQM B. V. Eindhoven. g Contact me: g J. M. M. van. Rooij@uu. nl g BBG 5. 07 (Tuesdays) g Directly after the lecture 2 Johan van Rooij

Teacher 2: Hans Bodlander g Professor in Utrecht g Head of the algorithms group. g Professor in Eindhoven g In Eindhoven on Mondays. g Contact me: g H. L. Bodlaender@uu. nl g 030 -2534409 g BBG 5. 03 (Thursday 15 -17) g Or, see if I’ve time. g Or, make an appointment by email. 3 Hans Bodlaender

What are we going to do today? g Part 1: g Algorithms and Networks: what and why? g Course organisation. g Euler tour example. g Part 2: g Lecture: stable marriage problem. 4

Algorithms and Networks WHAT AND WHY? 5

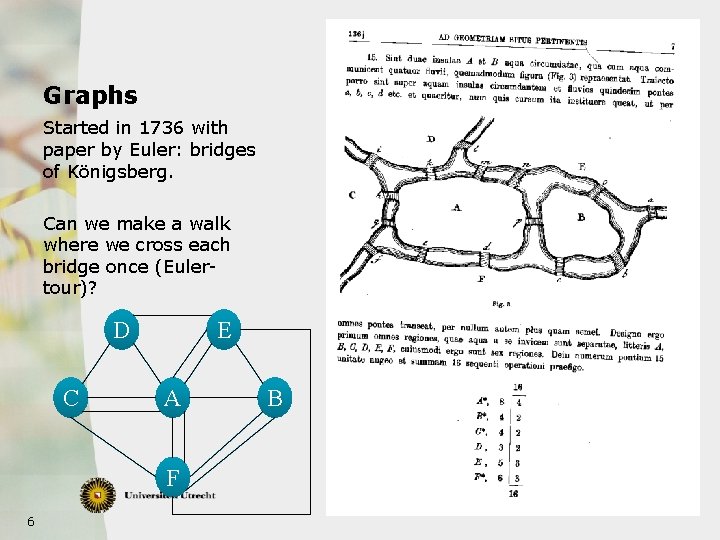
Graphs Started in 1736 with paper by Euler: bridges of Königsberg. Can we make a walk where we cross each bridge once (Eulertour)? D C E A F 6 B

Networks g Graphs are a (mathematical) model for many things in the real world: g Road networks, electrical networks, computer networks, organizational diagrams, social networks, structure of software, data base diagrams, … g Often real world problems have additional information. Then, the network is graph with some extra information such as: g Weights, lengths, distances, costs, time, … g Labels, sizes, names, … 7

Graph/network problems g Often, we want to compute something on the network, motivated from the application (or theoretical curiosity). g Examples: g Shortest path from A to B. g Maximum flow from A to B. g Does the graph have an Euler tour (all edges exactly once). g Does the graph have a Hamiltonian cycle (all nodes exactly once). g How good and fast can we let the computer do this computation? g Theoretical questions of algorithm design. g If fast algorithms exists, of high practical value. 8

Model and algorithm 1. Real-world problem. 2. Mathematical model of real-world problem. 3. Algorithm for mathematical model. 4. Solution produced by the algorithm. 5. Translation of solution to solution for real-world problem. 6. Check that the translated solution makes sense for the real- world problem. g If you do this for real problems for real customers, step 6 is often followed by designing a better model and returning to step 2. g This course is focusses on steps 3: algorithms. g But expects and practices also a little bit of step 2: modelling. 9

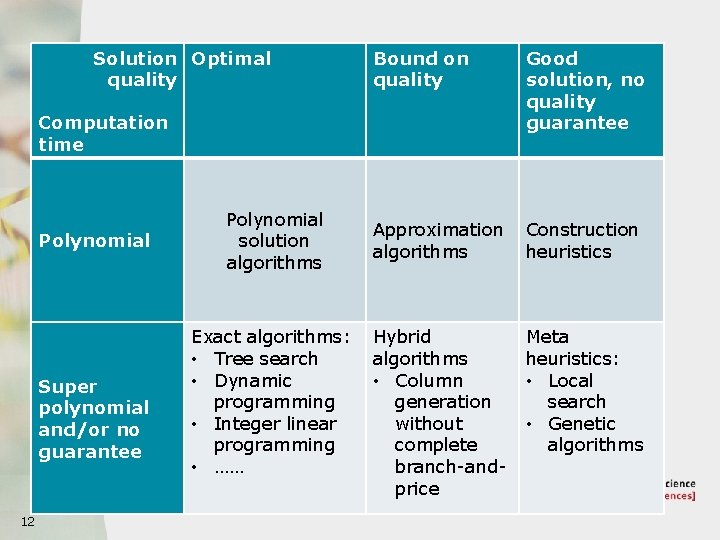
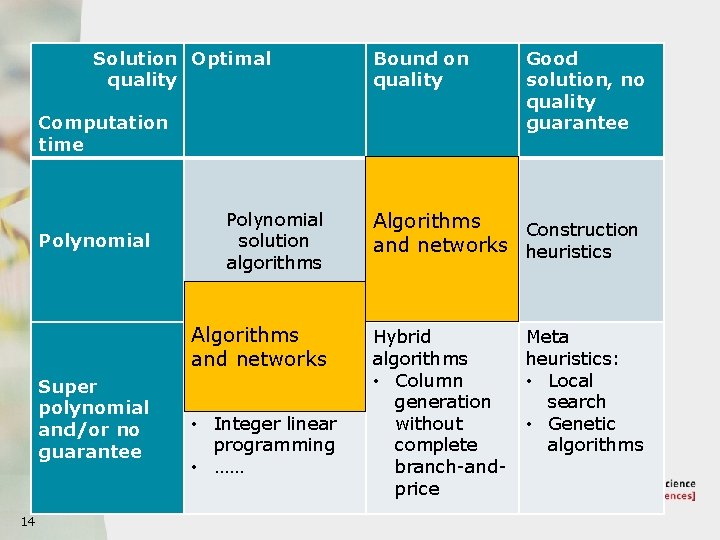
Algorithms and complexity g Algorithms g Exact, heuristic, approximation, special cases, … g Polynomial time, exponential time, … g Polynomial space, exponential space, … g Algorithms that parallelize well, or not, … g Complexity (asymptotic – O-notation) g Intrinsic difficulty of a problem. g NP-completeness, other complexity classes. g Approximation complexity (e. g. APX-completeness) g Fixed parameter tractability. g … 10

Algorithmic techniques g Combinatorial algorithms. g Mathematical programming. g (Integer) linear programming. g Quadratic programming. g Non-linear programming. g Pruning an exhaustive search tree. g Branch and bound. g Constraint programming. g Heuristics. g Greedy heuristics g Local search (iterative improvement, simulated annealing, tabu search, evolutionary algorithms, …) g … 11

Solution Optimal quality Bound on quality Good solution, no quality guarantee Approximation algorithms Construction heuristics Hybrid algorithms • Column generation without complete branch-andprice Meta heuristics: • Local search • Genetic algorithms Computation time Polynomial Super polynomial and/or no guarantee 12 Polynomial solution algorithms Exact algorithms: • Tree search • Dynamic programming • Integer linear programming • ……

Solution Optimal quality Bound on quality Good solution, no quality guarantee Approximation algorithms Construction heuristics Computation time Polynomial Super polynomial and/or no guarantee 13 Polynomial solution algorithms P Exact algorithms: • Tree search • Dynamic programming • Integer linear programming NPHybrid Meta algorithms hard heuristics: • Column generation without complete branch-andprice • Local search • Genetic algorithms

Solution Optimal quality Bound on quality Computation time Polynomial solution algorithms Algorithms Exact algorithms: • Tree search and networks Super polynomial and/or no guarantee 14 • Dynamic programming • Integer linear programming • …… Good solution, no quality guarantee Algorithms Approximation Construction and networks heuristics algorithms Hybrid algorithms • Column generation without complete branch-andprice Meta heuristics: • Local search • Genetic algorithms

Algorithms and Networks COURSE ORGANISATION 15

Algorithms and networks g 2 lectures per week. g Tuesday 9: 00 – 10: 45 by Johan van Rooij. g Thursday 13: 15 – 15: 00 by Hans Bodlaender. g Approximately 8 sets of exercises. g Two weeks time for handing them in. g 2 partial exams. g See the course website (www. cs. uu. nl/docs/vakken/an) for g Important updates on the course. g Slides. g Exercises. g Schedules. g Grades. g Etc. 16

Purpose of course g Knowing and being able to use and apply… g Important algorithmic techniques and research fields. g Important algorithms and their applications. g Analysis of algorithms. g The mathematics behind these concepts. g A little bit of algorithmic modelling. g In particular for combinatorial problems involving graphs and networks. 17

Topics of course (1) g Important polynomial-time algorithms. g Stable marriage. g Shortest paths. g Maximum flow. g Minimum cost flow. g Matching (bipartite, general graphs). g Dealing with hard problems, … 18

Topics of course (2) g Important polynomial-time algorithms, … g Dealing with hard problems, g Exact expontial-time algorithms. g Approximation algorithms and complexity. g Parameterized algorthms and complexity. g Kernelisation. g Treewidth. g Hard problems on resticted graph classes, e. g. , planar graphs. g Graph Isomorphism. 19

Final grade Final Grade = (Exercise set average) * 0. 3 + (Exam 1) * 0. 35 + (Exam 2) * 0. 35 g Assuming: g Exercise sets at least 6. 0. g Average exams at least 5. 0. g Details see webpage. 20

Studying this course g Visit the lectures! g Materials are scattered through literature: often hard to study at home if you were not at the course. g Make notes! g If you are not at the course: borrow/copy notes of other students. g Next to the lectures, you learn the most from the exercises. g Finish them before the corresponding exam, even when the deadline is later. g Topics in exercises that are not in the lectures are exam content! g Some books are recommended, but not necessary. g Use the powerpoints and pdf’s on the website. 21

Graded exercise sets g 8 sets (maybe 7 or 9) g You have two weeks for each set. g Every week a new exercise set will be handed out. g Hand in: g By e-mail: H. L. Bodlaender@uu. nl, include [AN 1], [AN 2] etc in the header of your e-mail. g Or, on paper during the lectures. g Or, on paper in Hans’ mailbox on the 5 th floor of the BBG. g Deadline: Monday 23: 59 hours. g After the deadline: grade = 0 (exception: joker rule) g Dutch or English g Write clear, legible, etc. g Unreadable, messy: grade = 0 22

On the exercise sets g Lots of work. . . , but you learn a lot. . . g Working in pairs: g OBLIGATORY, due to this years high number of students. g Both should have worked on and have understood all parts of what is handed in. g Allowed to mark parts as been done by one student. g Joker rule (write joker on your work or in your e-mail): g Twice during the course you can extend your deadline with three days (Monday 23: 59 becomes Thursday 23: 59). g Miss a third deadline: grade = 0. g Unless there are very special circumstances for all missed deadlines. 23

Workload g This course is 7. 5 ETCS. g This means 20 hour of work per week (officially). g Each week: g Two lectures on two different topics. g Making exercises – lots of work, but not that much. g Studying topics covered by the lectures yourself. g We go through a lot of material, so we recommend to study the material during the course, not only for the exams. 24

Are there. . . g Any questions on the organisation of the course? 25

Algorithms and Networks EULER TOUR EXAMPLE 26

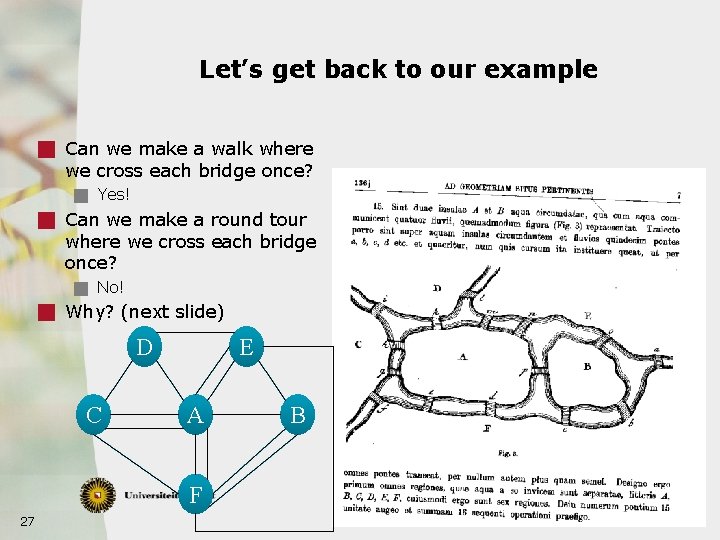
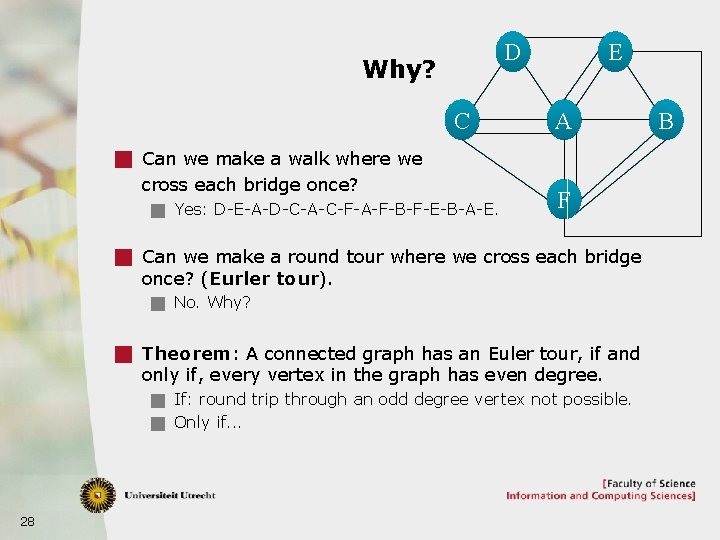
Let’s get back to our example g Can we make a walk where we cross each bridge once? g Yes! g Can we make a round tour where we cross each bridge once? g No! g Why? (next slide) D C E A F 27 B

D Why? C E A g Can we make a walk where we cross each bridge once? g Yes: D-E-A-D-C-A-C-F-A-F-B-F-E-B-A-E. F g Can we make a round tour where we cross each bridge once? (Eurler tour). g No. Why? g Theorem: A connected graph has an Euler tour, if and only if, every vertex in the graph has even degree. g If: round trip through an odd degree vertex not possible. g Only if. . . 28 B

If. . . proof continued g Lemma: If every vertex in a connected graph has even degree, then it has an Euler tour that can be found using the following algorithm: 1. From any starting vertex v build up any tour using unvisited edges until returning to v. g It is not possible to get stuck because all vertices have even degree before and after the tour visits the vertex. Hence the tour can only enter vertices of degree at least 2. While there exists unvisited edges, select a vertex u on the tour with unvisited edges. 3. Start another trail from u, following unused edges until returning to u, merge the two tours and return to step 2. g Again we cannot get stuck because of the same reason. 29

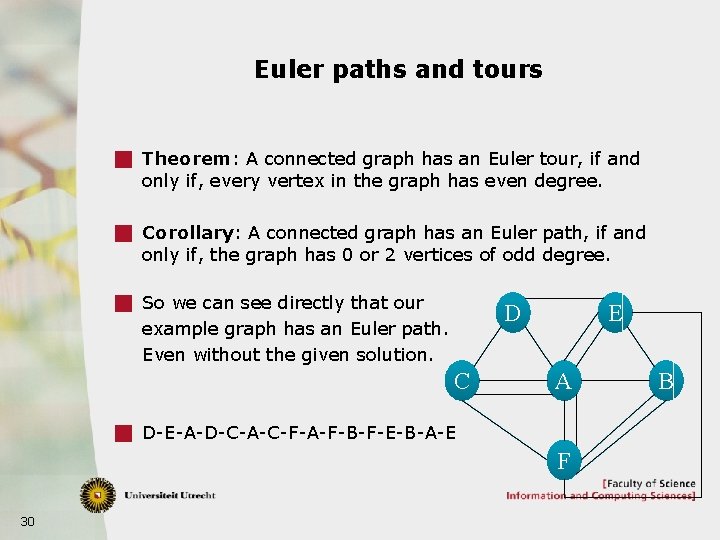
Euler paths and tours g Theorem: A connected graph has an Euler tour, if and only if, every vertex in the graph has even degree. g Corollary: A connected graph has an Euler path, if and only if, the graph has 0 or 2 vertices of odd degree. g So we can see directly that our D example graph has an Euler path. Even without the given solution. C E A g D-E-A-D-C-A-C-F-A-F-B-F-E-B-A-E F 30 B

Algorithms and Networks TIME FOR A BREAK. . . 31