ALGORITHMS AND FLOWCHARTS ALGORITHMS A typical programming task

ALGORITHMS AND FLOWCHARTS

ALGORITHMS �A typical programming task can be divided into two phases: �Problem solving phase ◦ produce an ordered sequence of steps that describe solution of problem ◦ this sequence of steps is called an algorithm �Implementation phase ◦ implement the program in some programming language

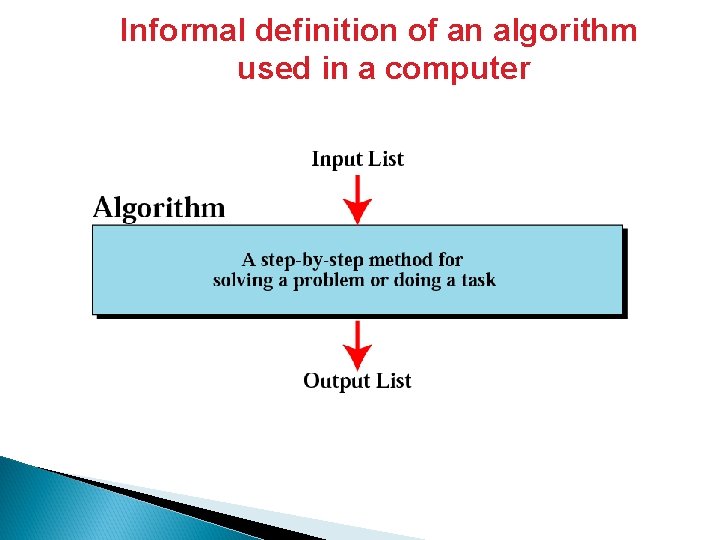
Informal definition of an algorithm used in a computer

Pseudo-Code � Pseudo-Code is simply a numbered list of instructions to perform some task. � Statements are written in simple English without regard to the final programming language. � Each instruction is written on a separate line. � The pseudo-code is the program-like statements written for human readers, not for computers. Thus, the pseudo-code should be readable by anyone who has done a little programming.

Basic Elements of Pseudo-code A Variable ◦ Having name and value ◦ There are two operations performed on a variable Assignment Operation is the one in which we associate a value to a variable. The other operation is the one in which at any given time we intend to retrieve the value previously assigned to that variable (Read Operation)

Basic Elements of Pseudo-code Assignment Operation ◦ This operation associates a value to a variable. ◦ While writing Pseudo-code you may follow your own syntax. ◦ Some of the possible syntaxes are: Assign 3 to x Set x equal to 3 x=3

Basic Operations of Pseudo-code Read Operation ◦ In this operation we intend to retrieve the value previously assigned to that variable. For example Set Value of x equal to y Read the input from user ◦ This operation causes the algorithm to get the value of a variable from the user. Get x Get a, b, c

Basic Operations of Pseudo-code Print the output to the user ◦ Print x (This will print value of variable x) ◦ Print “Your mileage is” x Carry out basic arithmetical computations ◦ Set x to 10 ◦ Set y to x*x/3

Steps in Problem Solving �First produce a general algorithm (one can use pseudocode) �Refine the algorithm successively to get step by step detailed algorithm that is very close to a computer language. �Pseudocode is an artificial and informal language that helps programmers develop algorithms. Pseudocode is very similar to everyday English.

Pseudocode & Algorithm � Example 1: Write an algorithm to determine a student’s final grade and indicate whether it is passing or failing. The final grade is calculated as the average of four marks.

Pseudocode & Algorithm Pseudocode: �Input a set of 4 marks �Calculate their average by summing and dividing by 4 �if average is below 50 Print “FAIL” else Print “PASS”

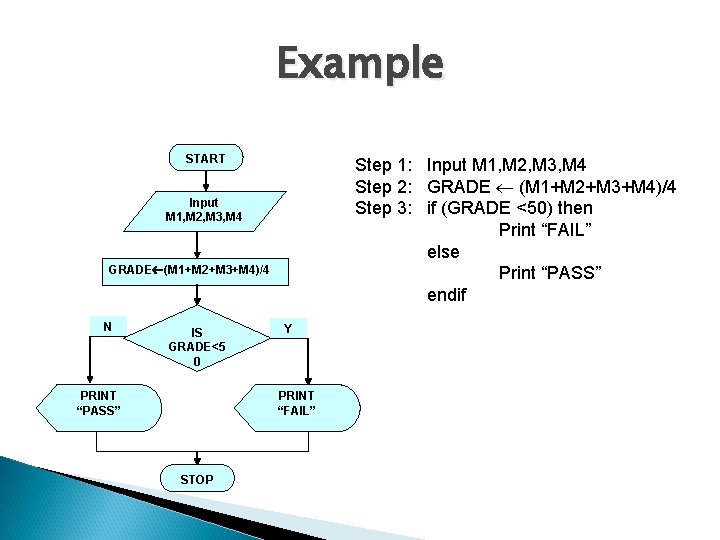
Pseudocode & Algorithm �Detailed Algorithm � Step 1: Input M 1, M 2, M 3, M 4 Step 2: GRADE (M 1+M 2+M 3+M 4)/4 Step 3: if (GRADE < 50) then Print “FAIL” else Print “PASS” endif

The Flowchart �A graphical representation of the sequence of operations in an information system or program. � Information system flowcharts show data flows from source documents through the computer to final distribution to users. � Program flowcharts show the sequence of instructions in a single program or subroutine. Different symbols are used to draw each type of flowchart.

The Flowchart A Flowchart ◦ shows logic of an algorithm ◦ emphasizes individual steps and their interconnections ◦ e. g. control flow from one action to the next

Flowchart Symbols

Example START Step 1: Input M 1, M 2, M 3, M 4 Step 2: GRADE (M 1+M 2+M 3+M 4)/4 Step 3: if (GRADE <50) then Print “FAIL” else Print “PASS” endif Input M 1, M 2, M 3, M 4 GRADE (M 1+M 2+M 3+M 4)/4 N IS GRADE<5 0 Y PRINT “FAIL” PRINT “PASS” STOP

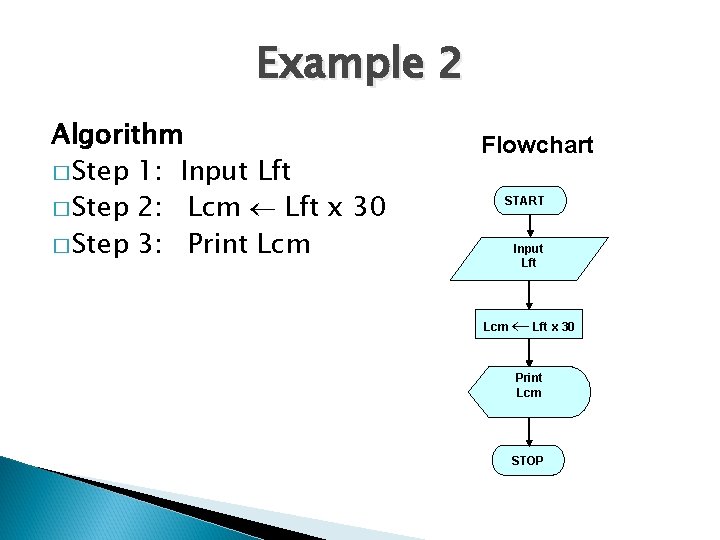
Example 2 � Write an algorithm and draw a flowchart to convert the length in feet to centimeter. Pseudocode: Input the length in feet (Lft) � Calculate the length in cm (Lcm) by multiplying LFT with 30 � Print length in cm (LCM) �

Example 2 Algorithm � Step 1: Input Lft � Step 2: Lcm Lft x 30 � Step 3: Print Lcm Flowchart START Input Lft Lcm Lft x 30 Print Lcm STOP

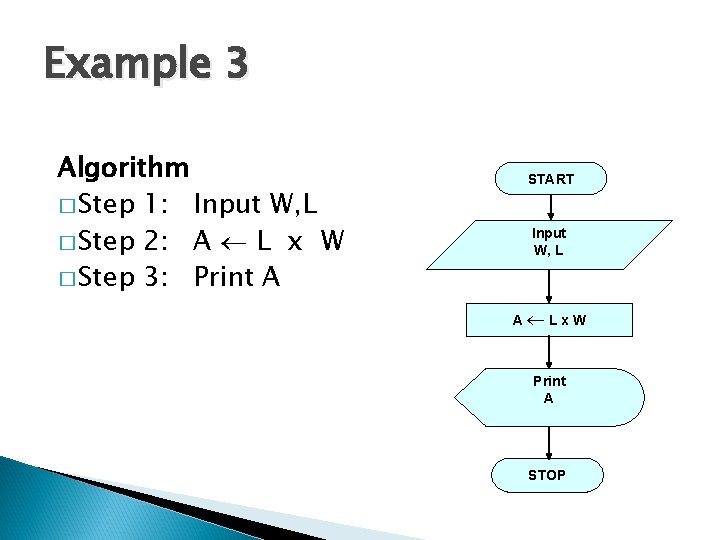
Example 3 Write an algorithm and draw a flowchart that will read the two sides of a rectangle and calculate its area. Pseudocode �Input the width (W) and Length (L) of a rectangle �Calculate the area (A) by multiplying L with W �Print A

Example 3 Algorithm � Step 1: Input W, L � Step 2: A L x W � Step 3: Print A START Input W, L A Lx. W Print A STOP

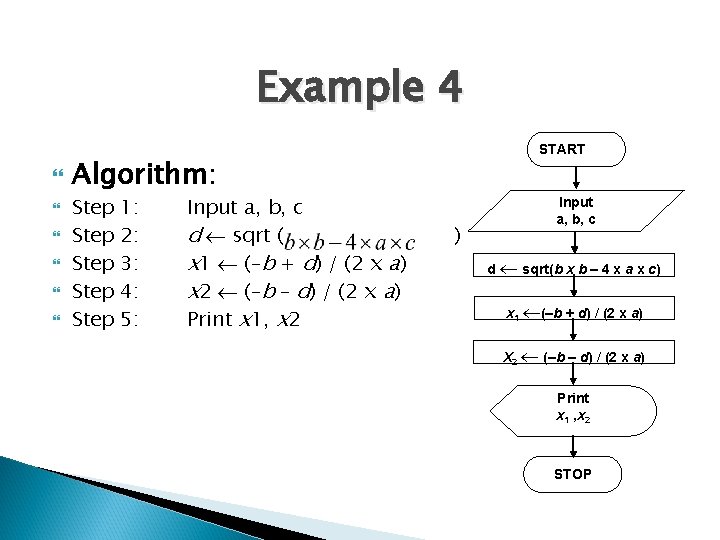
Example 4 Write an algorithm and draw a flowchart that will calculate the roots of a quadratic equation Hint: d = sqrt ( ), and the roots are: x 1 = (–b + d)/2 a and x 2 = (–b – d)/2 a

Example 4 Pseudocode: � Input the coefficients (a, b, c) of the quadratic equation � Calculate d � Calculate x 1 � Calculate x 2 � Print x 1 and x 2

Example 4 START Algorithm: Step Step 1: 2: 3: 4: 5: Input a, b, c d sqrt ( x 1 (–b + d) / (2 x a) x 2 (–b – d) / (2 x a) Print x 1, x 2 ) Input a, b, c d sqrt(b x b – 4 x a x c) x 1 (–b + d) / (2 x a) X 2 (–b – d) / (2 x a) Print x 1 , x 2 STOP

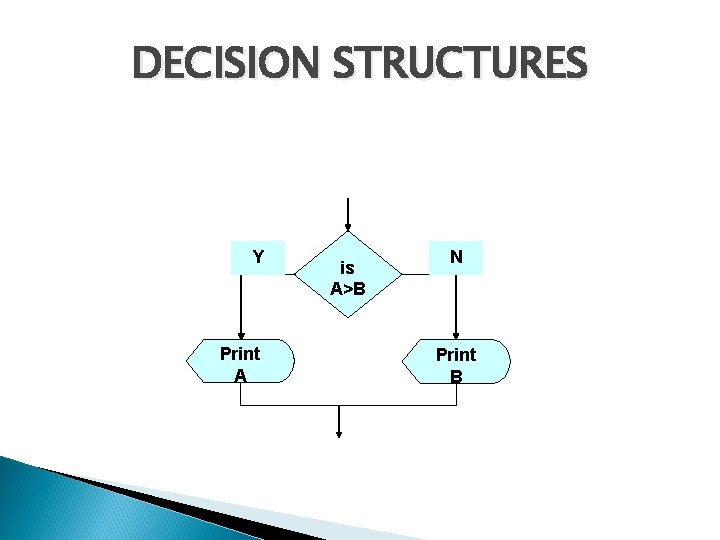
DECISION STRUCTURES �The �it expression A>B is a logical expression describes a condition we want to test �if A>B is true (if A is greater than B) we take the action on left �print the value of A �print the value of B �if A>B is false (if A is not greater than B) we take the action on right

DECISION STRUCTURES Y Print A is A>B N Print B

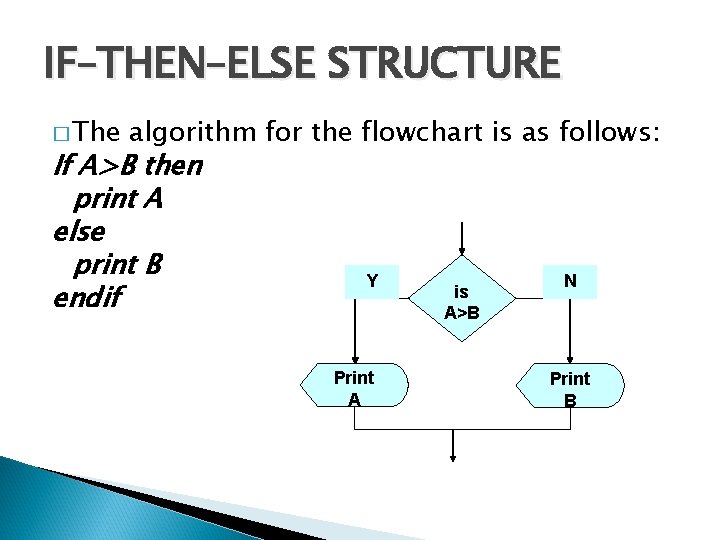
IF–THEN–ELSE STRUCTURE � The structure is as follows If condition then true alternative else false alternative endif

IF–THEN–ELSE STRUCTURE � The algorithm for the flowchart is as follows: If A>B then print A else print B endif Y Print A is A>B N Print B

Relational Operators Operator Description > Greater than < Less than = Equal to Greater than or equal to Less than or equal to Not equal to

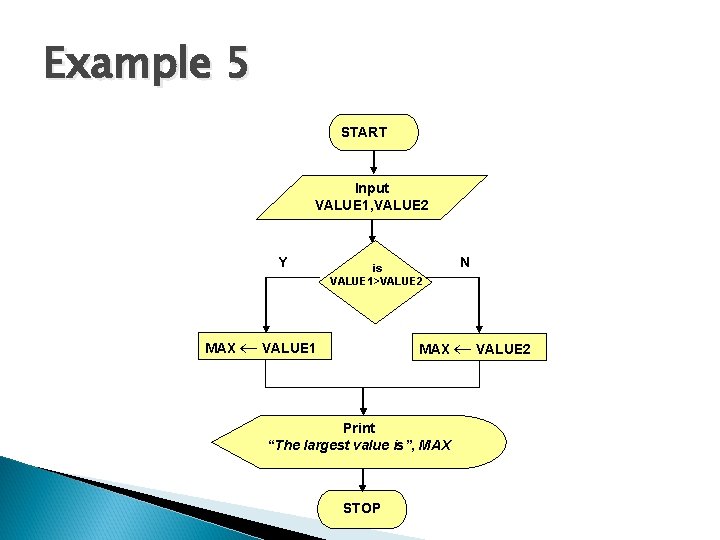
Example 5 � Write an algorithm that reads two values, determines the largest value and prints the largest value with an identifying message. ALGORITHM Step 1: Input VALUE 1, VALUE 2 Step 2: if (VALUE 1 > VALUE 2) then MAX VALUE 1 else Step 3: MAX VALUE 2 endif Print “The largest value is”, MAX

Example 5 START Input VALUE 1, VALUE 2 Y is VALUE 1>VALUE 2 MAX VALUE 1 N MAX VALUE 2 Print “The largest value is”, MAX STOP

NESTED IFS � One of the alternatives within an IF–THEN– ELSE statement ◦ may involve further IF–THEN–ELSE statement

Example 6 � Write an algorithm that reads three numbers and prints the value of the largest number.

Example 6 Step 1: Input N 1, N 2, N 3 Step 2: if (N 1>N 2) then if (N 1>N 3) then MAX N 1 [N 1>N 2, N 1>N 3] else MAX N 3 [N 3>N 1>N 2] MAX N 2 [N 2>N 1, N 2>N 3] endif else if (N 2>N 3) then else MAX N 3 [N 3>N 2>N 1] endif Step 3: Print “The largest number is”, MAX