Algorithms and Complexity Algorithms Growth of Functions Algorithm

강의 내용 Algorithms and Complexity 알고리즘(Algorithms) 함수의 증가(Growth of Functions) 알고리즘 복잡도(Algorithm Complexity) Page 2 Discrete Mathematics by Yang-Sae Moon

Algorithms The foundation of computer programming. (컴퓨터 프로그래밍의 기초/기반이다. ) Most generally, an algorithm just means a definite procedure for performing some sort of task. (알고리즘은 주어진 일을 수행하기 위한 정의된 절차를 의미한다. ) A computer program is simply a description of an algorithm in a language precise enough for a computer to understand. (컴퓨터 프로그램이란 정의된 알고리즘을 컴퓨터가 이해할 수 있는 언어 로 정확하게 기술한 것에 불과하다. ) We say that a program implements (or “is an implementation of”) its algorithm. (프로그램은 알고리즘을 “구현한 것이다”라고 이야기한다. ) Page 3 Discrete Mathematics by Yang-Sae Moon

Programming Languages Algorithms Some common programming languages: • Newer: Java, C, C++, Visual Basic, Java. Script, Perl, Tcl, Pascal • Older: Fortran, Cobol, Lisp, Basic • Assembly languages, for low-level coding. In this class we will use an informal, Pascal-like “pseudocode” language. You should know at least 1 real language! Page 4 Discrete Mathematics by Yang-Sae Moon

Algorithm Example (in English) Algorithms Task: Given a sequence {ai}=a 1, …, an, ai N, say what its largest element is. (주어진 sequence에서 가장 큰 수는? ) Algorithm in English • Set the value of a temporary variable v to a 1’s value. • Look at the next element ai in the sequence. • If ai>v, then re-assign v to the number ai. • Repeat previous 2 steps until there are no more elements in the sequence, & return v. Page 5 Discrete Mathematics by Yang-Sae Moon

Executing an Algorithms When you start up a piece of software, we say the program or its algorithm are being run or executed by the computer. (소프트웨어를 시작할 때, 우리는 프로그램 혹은 알고리즘을 실행한다( 혹은 돌린다)라고 이야기한다. ) Given a description of an algorithm, you can also execute it by hand(? ), by working through all of its steps on paper. (알고리즘이 있으면, 종이에 손으로 써 가면서 이를 수행할 수도 있다. ) Before ~WWII, “computer” meant a person whose job was to run algorithms! (2차 대전 이전에, 컴퓨터는 알고리즘을 수행하는 사람을 의미했다!) Page 6 Discrete Mathematics by Yang-Sae Moon

Execute the Max Algorithms Let {ai}=7, 12, 3, 15, 8. Find its maximum… by hand. Set v = a 1 = 7. Look at next element: a 2 = 12. Is a 2>v? Yes, so change v to 12. Look at next element: a 3 = 3. Is 3>12? No, leave v alone…. Is 15>12? Yes, v=15… Page 7 Discrete Mathematics by Yang-Sae Moon

Algorithm Characteristics (알고리즘의 특성) (1/2) Algorithms Some important features of algorithms: Input(입력): Information or data that comes in. Output(출력): Information or data that goes out. Definiteness(명확성): Precisely defined. (각 단계는 명확하게 정의되어야 한다. ) Correctness(정확성): Outputs correctly relate to inputs. (입력 값의 각 집합에 대해서 정확한 출력 값을 만들어야 한다. ) Finiteness(유한성): Won’t take forever to describe or run. Page 8 Discrete Mathematics by Yang-Sae Moon

Algorithm Characteristics (알고리즘의 특성) (2/2) Algorithms Some important features of algorithms (계속): Effectiveness(효율성): Individual steps are all do-able. (각 단계는 유한한 양의 시간에 수행되어야 한다. ) Generality(일반성): Works for many possible inputs. (특정한 입력이 아닌 모든 가능한 입력에 대해서 동작하여야 한다. ) Page 9 Discrete Mathematics by Yang-Sae Moon

Pseudocode Language procedure name(argument: type) variable : = expression informal statement begin statements end {comment} if condition then statement [else statement] Algorithms for variable : = initial value to final value statement while condition statement procname(arguments) Not defined in book: return expression Page 10 Discrete Mathematics by Yang-Sae Moon

procedure procname(arg: type) Algorithms Declares that the following text defines • a procedure named procname that takes • inputs (arguments) named arg which are • data objects of the type. Example: procedure maximum(L: list of integers) [statements defining maximum…] Page 11 Discrete Mathematics by Yang-Sae Moon

variable : = expression Algorithms An assignment statement evaluates the expression, then reassigns the variable to the value that results. • Example: v : = 3 x+7 (If x is 2, changes v to 13. ) In pseudocode, the expression might be informal: • x : = the largest integer in the list L Page 12 Discrete Mathematics by Yang-Sae Moon

Informal Statement Algorithms Sometimes we may write an informal statement, if the meaning is still clear and precise: “swap x and y. ” Keep in mind that real programming languages never allow this. (궁극적으로는 알고리즘을 쓰고 이를 구현해야 한다. ) When we ask for an algorithm to do so-and-so, writing “Do so-and-so” isn’t enough! (“x를 찾는 알고리즘을 기술하라”했는데, “find x”라 하는 것은 충분치 않다!) • Break down algorithm into detailed steps. Page 13 Discrete Mathematics by Yang-Sae Moon

begin statements end Algorithms Groups a sequence of statements together: Allows sequence to be used like a single statement. Might be used: • After a procedure declaration. • In an if statement after then or else. • In the body of a for or while loop. begin statement 1 statement 2 … statement n end Page 14 Discrete Mathematics by Yang-Sae Moon

{ comment } Algorithms Not executed (does nothing). Natural-language text explaining some aspect of the procedure to human readers. (Reader의 이해 도모) Also called a remark in some real programming languages. Example: • {Note that v is the largest integer seen so far. } Page 15 Discrete Mathematics by Yang-Sae Moon

If condition then statement Algorithms Evaluate the propositional expression condition. If the resulting truth value is true, then execute the statement; otherwise, just skip on ahead to the next statement. (조건이 true일 때만 문장을 수행한다. ) Variant: if cond then stmt 1 else stmt 2 Like before, but iff truth value is false, executes stmt 2. Page 16 Discrete Mathematics by Yang-Sae Moon

while condition statement (1/2) Algorithms Evaluate the propositional expression condition. If the resulting value is true, then execute statement. Continue repeating the above two actions over and over until finally the condition evaluates to false; then go on to the next statement. (조건이 true인 한 문장을 반복하여 수행한다. ) Page 17 Discrete Mathematics by Yang-Sae Moon

while comment statement (2/2) Algorithms Also equivalent to infinite nested ifs, like so: (if를 무한히 써서 구현할 수도 있다…. 설마~) if condition begin statement …(continue infinite nested if’s) end Page 18 Discrete Mathematics by Yang-Sae Moon

for var : = initial to final stmt Algorithms Initial is an integer expression. Final is another integer expression. Repeatedly execute stmt, first with variable var : = initial, then with var : = initial+1, then with var : = initial+2, etc. , then finally with var : = final. What happens if stmt changes the value that initial or final evaluates to? For can be exactly defined in terms of while, like so: Page 19 begin var : = initial while var final begin stmt var : = var + 1 end Discrete Mathematics by Yang-Sae Moon

procedure(argument) Algorithms A procedure call statement invokes the named procedure, giving it as its input the value of the argument expression. Various real programming languages refer to procedures as • functions (since the procedure call notation works similarly to function application f(x)), or as • subroutines, subprograms, or methods. Page 20 Discrete Mathematics by Yang-Sae Moon

Max Procedure in Pseudocode Algorithms Rewrite “finding maximum number” in pseudocode. procedure max(a 1, a 2, …, an: integers) v : = a 1 {largest element so far} for i : = 2 to n {go thru rest of elems} if ai > v then v : = ai {found bigger? } {at this point v’s value is the same as the largest integer in the list} procedure max(a 1, a 2, …, an: integers) return v v : = a 1 for i : = 2 to n if ai > v then v : = ai return v Page 21 Discrete Mathematics by Yang-Sae Moon

Inventing an Algorithms Requires a lot of creativity and intuition. • Like writing proofs. We can’t give you an algorithm for inventing algorithms. • Just look at lots of examples… [많은 예를 보세요…] • And practice (preferably, on a computer) [연습을 많이 하세요…] • And look at more examples… [좀 더 많은 예를 보세요…] • And practice some more… etc. , etc. [좀 더 많은 연습을 하세요…] Page 22 Discrete Mathematics by Yang-Sae Moon

Searching Algorithm (탐색 알고리즘) Algorithms Problem of searching an ordered list. (정렬된 리스트에서 주어진 값을 찾아내는 검색을 수행하는 문제) • Given a list L of n elements that are sorted into a definite order (e. g. , numeric, alphabetical), • And given a particular element x, • Determine whether x appears in the list, • and if so, return its index (position) in the list. Problem occurs often in many contexts. (여러 분이 Programming을 하는 한 수십 번 이상 마주치는 문제임!) Let’s find an efficient algorithm! Page 23 Discrete Mathematics by Yang-Sae Moon

Linear Search (선형 탐색) Algorithms 리스트의 첫 번째 원소부터 차례대로 검색하는 방법 예: Find ‘ 12’ in {3, 6, 9, 12, 15, 18, 21, 24} procedure linear search (x: integer, a 1, a 2, …, an: distinct integers) i : = 1 while (i n x ai) i : = i + 1 if i n then location : = i else location : = 0 return location {index or 0 if not found} Linear search는 ordered list(정렬된 상태)뿐 아니라 unordered list(정렬 되지 않은 상태)에서도 바르게 동작한다. Page 24 Discrete Mathematics by Yang-Sae Moon

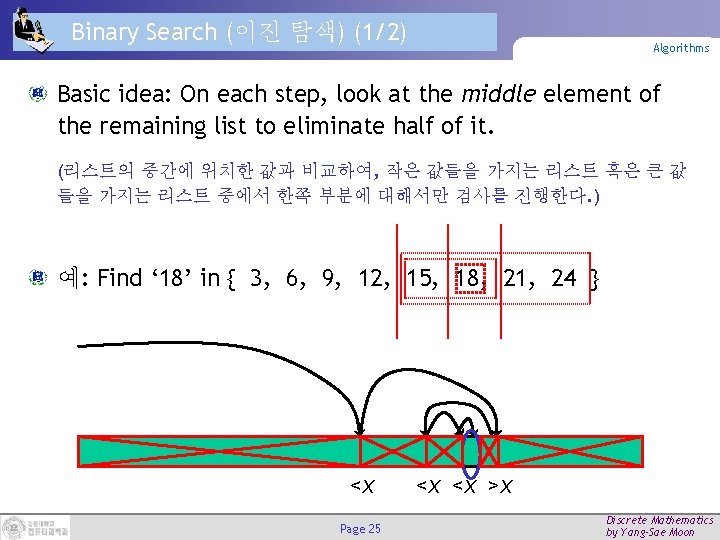
Binary Search (이진 탐색) (1/2) Algorithms Basic idea: On each step, look at the middle element of the remaining list to eliminate half of it. (리스트의 중간에 위치한 값과 비교하여, 작은 값들을 가지는 리스트 혹은 큰 값 들을 가지는 리스트 중에서 한쪽 부분에 대해서만 검사를 진행한다. ) 예: Find ‘ 18’ in { 3, 6, 9, 12, 15, 18, 21, 24 } <x Page 25 <x <x >x Discrete Mathematics by Yang-Sae Moon

Binary Search (이진 탐색) (2/2) Algorithms procedure binary search (x: integer, a 1, a 2, …, an: distinct integers) i : = 1 {left endpoint of search interval} j : = n {right endpoint of search interval} while i<j begin {while interval has >1 item} m : = (i+j)/2 {midpoint} if x>am then i : = m+1 else j : = m end if x = ai then location : = i else location : = 0 return location Binary search는 ordered list(정렬된 상태)에서만 바르게 동작할 뿐 unordered list(정렬되지 않은 상태)에서는 바르게 동작하지 않는다. Page 26 Discrete Mathematics by Yang-Sae Moon

Sorting Algorithm (정렬 알고리즘) Algorithms Sorting is a common operation in many applications. (Programming을 하는 한 Search 다음으로 많이 마주치는 문제임!) • E. g. spreadsheets and databases It is also widely used as a subroutine in other dataprocessing algorithms. Two sorting algorithms shown in textbook: • Bubble sort • Insertion sort However, these are not very efficient, and you should not use them on large data sets! There are more than 15 different sorting algorithms! (“The Art of Computer Programming” by Donald Knuth. ) Page 27 Discrete Mathematics by Yang-Sae Moon

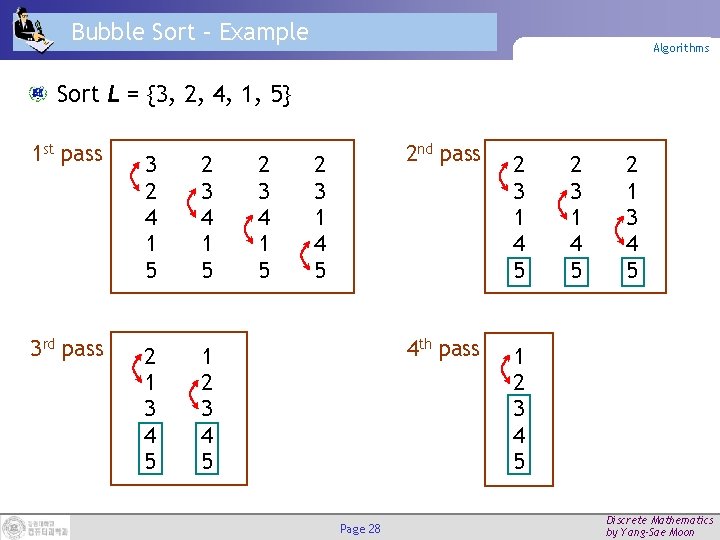
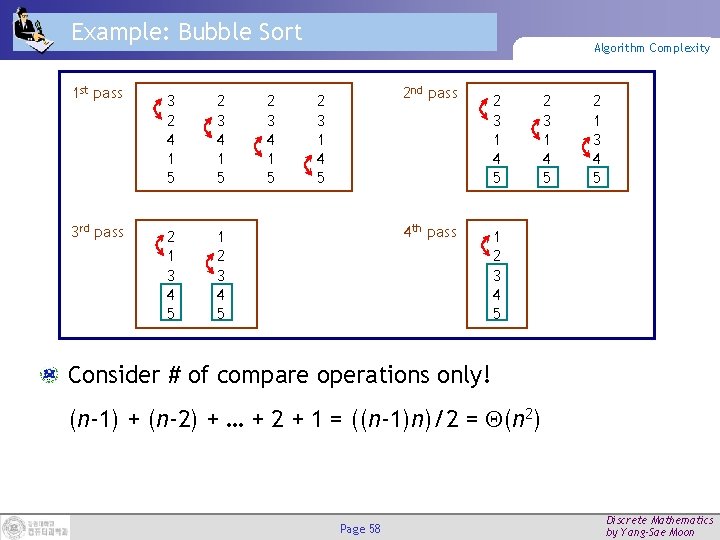
Bubble Sort – Example Algorithms Sort L = {3, 2, 4, 1, 5} 1 st pass 3 rd pass 3 2 4 1 5 2 3 4 1 5 2 1 3 4 5 1 2 3 4 5 2 3 4 1 5 2 nd pass 2 3 1 4 5 4 th pass Page 28 2 3 1 4 5 2 1 3 4 5 1 2 3 4 5 Discrete Mathematics by Yang-Sae Moon

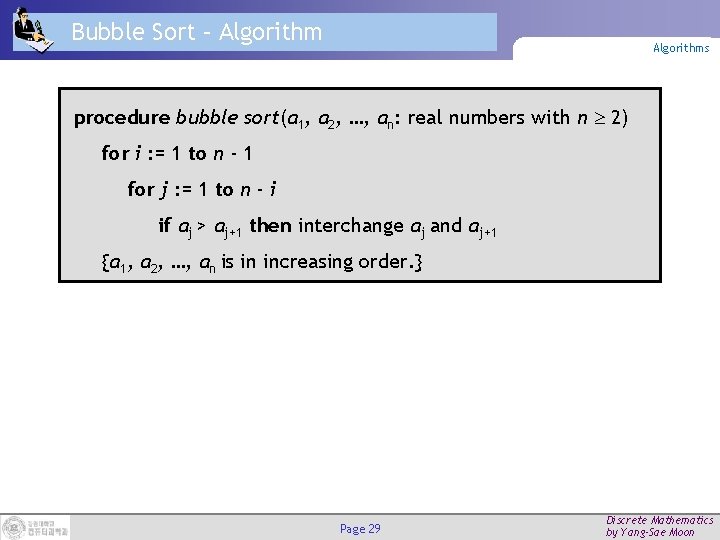
Bubble Sort – Algorithms procedure bubble sort(a 1, a 2, …, an: real numbers with n 2) for i : = 1 to n - 1 for j : = 1 to n - i if aj > aj+1 then interchange aj and aj+1 {a 1, a 2, …, an is in increasing order. } Page 29 Discrete Mathematics by Yang-Sae Moon

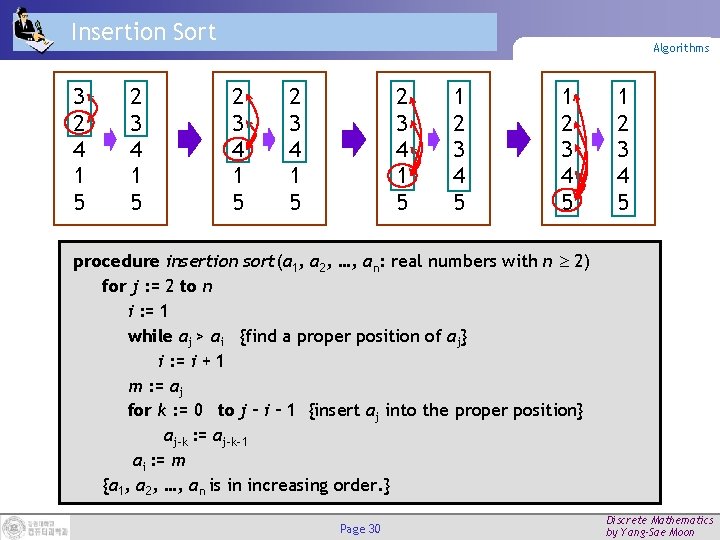
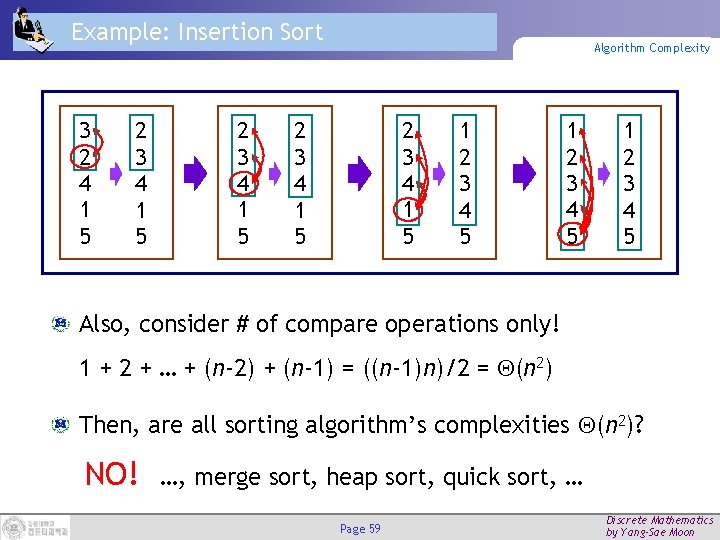
Insertion Sort 3 2 4 1 5 2 3 4 1 5 Algorithms 2 3 4 1 5 1 2 3 4 5 procedure insertion sort(a 1, a 2, …, an: real numbers with n 2) for j : = 2 to n i : = 1 while aj > ai {find a proper position of aj} i : = i + 1 m : = aj for k : = 0 to j – i – 1 {insert aj into the proper position} aj-k : = aj-k-1 ai : = m {a 1, a 2, …, an is in increasing order. } Page 30 Discrete Mathematics by Yang-Sae Moon

강의 내용 Algorithms and Complexity 알고리즘(Algorithms) 함수의 증가(Growth of Functions) 알고리즘 복잡도(Algorithm Complexity) Page 32 Discrete Mathematics by Yang-Sae Moon

Orders of Growth – Introduction Growth of Functions For functions over numbers, we often need to know a rough measure of how fast a function grows. (과연 함수는 얼마나 빨리 증가하는가? ) If f(x) is faster growing than g(x), then f(x) always eventually becomes larger than g(x) in the limit (for large enough values of x). (f(x)가 g(x)보다 빨리 증가한다면, 궁극적으로 f(x)의 값이 g(x)의 값보다 커진다. ) Page 33 Discrete Mathematics by Yang-Sae Moon

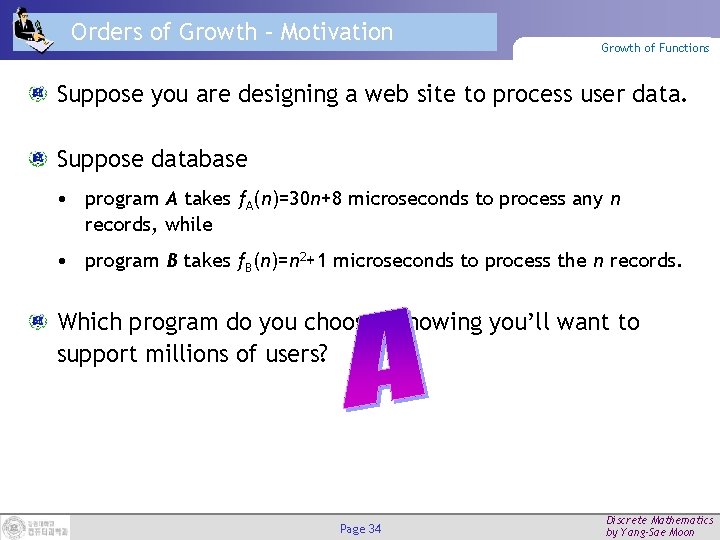
Orders of Growth – Motivation Growth of Functions Suppose you are designing a web site to process user data. Suppose database • program A takes f. A(n)=30 n+8 microseconds to process any n records, while • program B takes f. B(n)=n 2+1 microseconds to process the n records. Which program do you choose, knowing you’ll want to support millions of users? Page 34 Discrete Mathematics by Yang-Sae Moon

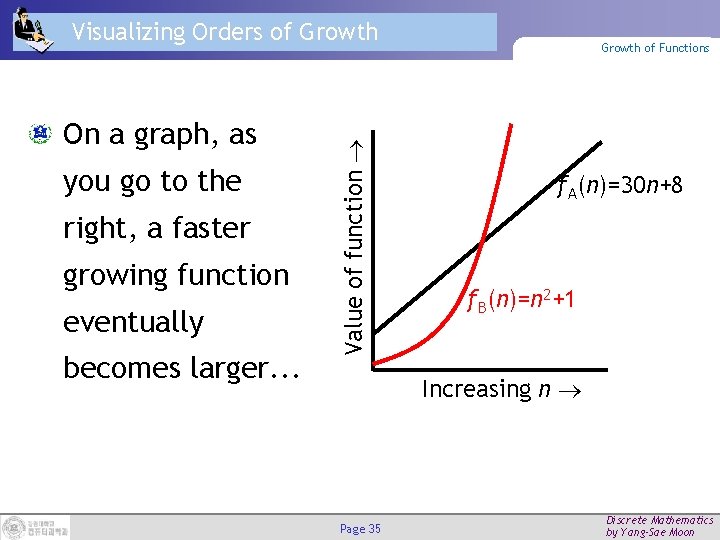
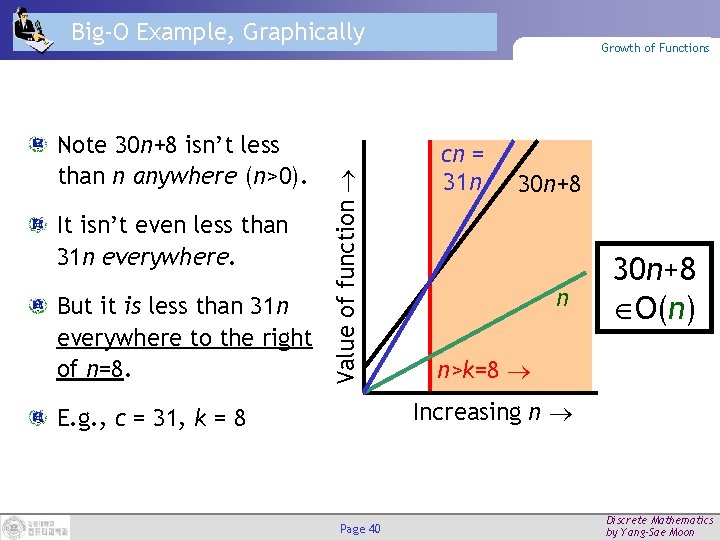
On a graph, as you go to the right, a faster growing function eventually becomes larger. . . Value of function Visualizing Orders of Growth of Functions f. A(n)=30 n+8 f. B(n)=n 2+1 Increasing n Page 35 Discrete Mathematics by Yang-Sae Moon

Concept of Orders of Growth of Functions We say f. A(n)=30 n+8 is order n, or O(n). It is, at most, roughly proportional to n. f. B(n)=n 2+1 is order n 2, or O(n 2). It is roughly proportional to n 2. Any O(n 2) function is faster-growing than any O(n) function. For large numbers of user records, the O(n 2) function will always take more time. Page 36 Discrete Mathematics by Yang-Sae Moon

Definition: O(g), at most order g Growth of Functions Let g be any function R R. Define “at most order g”, written O(g), to be: {f: R R | c, k: x>k: f(x) cg(x)}. • “Beyond some point k, function f is at most a constant c times g (i. e. , proportional to g). ” • (x > k일 때, f(x) cg(x)를 만족하는 c, k가 존재하면, f는 O(g)라 한다. ) “f is at most order g”, or “f is O(g)”, or “f=O(g)” all just mean that f O(g). Sometimes the phrase “at most” is omitted. (일반적으로 그냥 “오더 g”라 이야기한다. ) Page 37 Discrete Mathematics by Yang-Sae Moon

Points about the Definition Growth of Functions Note that f is O(g) so long as any values of c and k exist that satisfy the definition. But: The particular c, k, values that make the statement true are not unique: Any larger value of c and/or k will also work. (조건을 만족하는 c, k는 여러 개 있을 수 있다. ) You are not required to find the smallest c and k values that work. (Indeed, in some cases, there may be no smallest values!) (조건을 만족하는 가장 작은 c, k를 찾을 필요는 없다. 보여주기만 하면 된다. ) However, you should prove that the values you choose do work. (증명하기 위해서는 만족하는 c, k를 하나는 찾아야 한다. ) Page 38 Discrete Mathematics by Yang-Sae Moon

“Big-O” Proof Example Growth of Functions Show that 30 n+8 is O(n). • Show c, k: n>k: 30 n+8 cn. • Let c=31, k=8. Assume n>k(=8). • Then cn = 31 n = 30 n + n > 30 n+8, so 30 n+8 < cn. Show that n 2+1 is O(n 2). • Show c, k: n>k: n 2+1 cn 2. • Let c=2, k=1. Assume n>1. • Then cn 2 = 2 n 2 = n 2+n 2 > n 2+1, or n 2+1< cn 2. Page 39 Discrete Mathematics by Yang-Sae Moon

Note 30 n+8 isn’t less than n anywhere (n>0). It isn’t even less than 31 n everywhere. But it is less than 31 n everywhere to the right of n=8. Value of function Big-O Example, Graphically Growth of Functions cn = 31 n 30 n+8 O(n) n>k=8 Increasing n E. g. , c = 31, k = 8 Page 40 Discrete Mathematics by Yang-Sae Moon

Examples of Big-O (1/2) Growth of Functions f(x) = anxn + an-1 xn-1 + … + a 1 x + a 0 • f(x) = anxn + an-1 xn-1 + … + a 1 x + a 0 |an|xn + |an-1|xn-1 + … + |a 1|x + |a 0| = xn(|an| + |an-1|/x + … + |a 1|/xn-1 + |a 0|/xn) xn(|an| + |an-1| + … + |a 1| + |a 0|) = cxn = O(xn) c f(n) = 1 + 2 + 3 + … + n • f(n) = 1 + 2 + 3 + … + n n+n+n+…+n = n 2 = O(n 2) Page 41 Discrete Mathematics by Yang-Sae Moon

Examples of Big-O (2/2) Growth of Functions f(n) = n! • f(n) = n! = n∙(n-1)∙(n-2)∙…∙ 3∙ 2∙ 1 n∙n∙n∙…∙n∙n∙n = nn = O(nn) f(n) = log(n!) • f(n) = log(n!) log(nn) = nlogn = O(nlogn) Page 42 Discrete Mathematics by Yang-Sae Moon

Useful Facts about Big-O (1/2) Growth of Functions Big O, as a relation, is transitive: f O(g) g O(h) f O(h) Sums of functions: If g O(f) and h O(f), then g+h O(f). c>0, O(cf)=O(f+c)=O(f) • E. g. , O(2 x 2) = O(x 2+2) = O(x 2 -3) = O(x 2) If f 1=O(g 1) and f 2 = O(g 2), then f 1+f 2 = O(max(g 1, g 2)) • E. g. , if f 1(x) = x 2 = O(x 2), f 2(x) = x 3 = O(x 3), then (f 1+f 2)(x) = x 2 + x 3 = O(x 3) = O(max(x 2, x 3)) Page 43 Discrete Mathematics by Yang-Sae Moon

Useful Facts about Big-O (2/2) Growth of Functions f 1=O(g 1) and f 2 = O(g 2), then f 1 f 2 = O(g 1 g 2) • E. g. , if f 1(x) = x 2 = O(x 2), f 2(x) = x 3 = O(x 3), then (f 1 f 2)(x) = x 2∙x 3 = x 5 = O(x 5) = O(x 2∙x 3)) Other useful facts… • f, g & constants a, b R, with b 0, - af = O(f) - f+O(f) = O(f) (e. g. 3 x 2 = O(x 2)) (e. g. x 2+x = O(x 2)) • Also, the followings hold (그냥 참고하세요): - |f|1 -b = O(f); (logb |f|)a = O(f) g=O(fg) fg O(g) a=O(f) (e. g. x 1 = O(x)) log x = O(x)) x = O(x log x)) x log x O(x)) 3 = O(x)) Page 44 Discrete Mathematics by Yang-Sae Moon

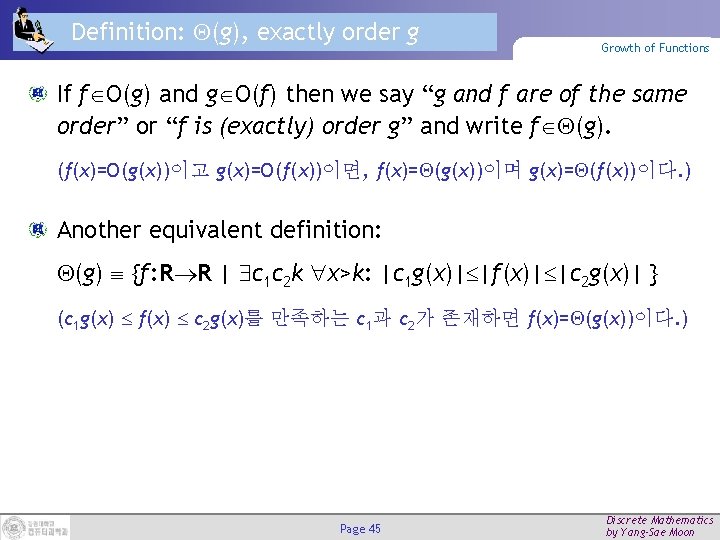
Definition: (g), exactly order g Growth of Functions If f O(g) and g O(f) then we say “g and f are of the same order” or “f is (exactly) order g” and write f (g). (f(x)=O(g(x))이고 g(x)=O(f(x))이면, f(x)= (g(x))이며 g(x)= (f(x))이다. ) Another equivalent definition: (g) {f: R R | c 1 c 2 k x>k: |c 1 g(x)| |f(x)| |c 2 g(x)| } (c 1 g(x) f(x) c 2 g(x)를 만족하는 c 1과 c 2가 존재하면 f(x)= (g(x))이다. ) Page 45 Discrete Mathematics by Yang-Sae Moon

Rules for Growth of Functions Mostly like rules for O( ), except: f, g>0 & constants a, b R, af (f), but f (fg) unless g= (1) |f|1 -b (f), and (logb|f|)c (f). with b>0, Same as with O. Unlike with O. (참고) Page 46 Discrete Mathematics by Yang-Sae Moon

Examples of (1/2) Growth of Functions f(n) = 1 + 2 + 3 + … + n = (n 2)? • f(n) = 1 + 2 + 3 + … + n n+n+n+…+n = n 2 • f(n) = 1 + 2 + 3 + … + n = (n∙(n + 1))/2 = n 2/2 + n/2 n 2/2 • n 2/2 f(n) n 2, i. e. , c 1 = ½, c 2 = 1 f(n) = (n 2) Page 47 Discrete Mathematics by Yang-Sae Moon

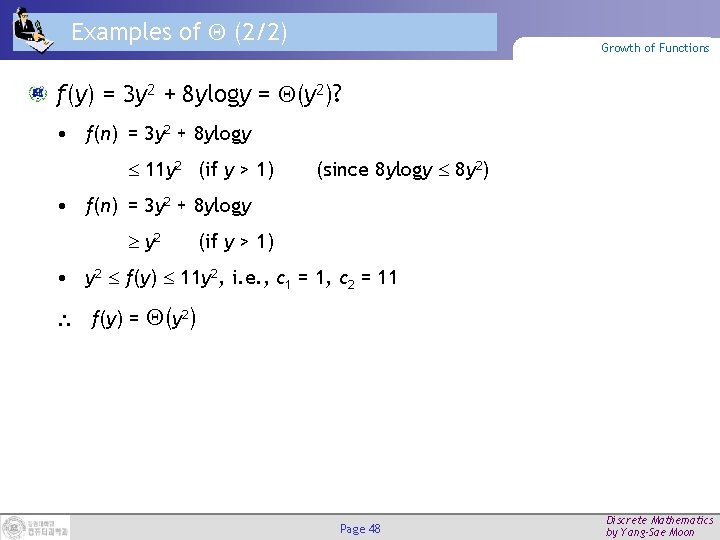
Examples of (2/2) Growth of Functions f(y) = 3 y 2 + 8 ylogy = (y 2)? • f(n) = 3 y 2 + 8 ylogy 11 y 2 (if y > 1) (since 8 ylogy 8 y 2) • f(n) = 3 y 2 + 8 ylogy y 2 (if y > 1) • y 2 f(y) 11 y 2, i. e. , c 1 = 1, c 2 = 11 f(y) = (y 2) Page 48 Discrete Mathematics by Yang-Sae Moon

강의 내용 Algorithms and Complexity 알고리즘(Algorithms) 함수의 증가(Growth of Functions) 알고리즘 복잡도(Algorithm Complexity) Page 49 Discrete Mathematics by Yang-Sae Moon

What is Algorithm Complexity? Algorithm Complexity The algorithmic complexity of a computation is some measure of how difficult it is to perform the computation. (문제 계산(computation)이 얼마나 어려운가를 나타내는 측정치이다. ) Measures some aspect of cost of computation (in a general sense of cost). (계산을 위한 비용에 대한 측정치이다. ) Common complexity measures: • Time complexity: # of operations or steps required • Space complexity: # of memory bits required Page 50 Discrete Mathematics by Yang-Sae Moon

Complexity Depends on Input Algorithm Complexity Most algorithms have different complexities for inputs of different sizes. (E. g. searching a long list takes more time than searching a short one. ) (대부분의 알고리즘은 입력의 크기에 따라 복잡도가 달라진다. 당연!) Therefore, complexity is usually expressed as a function of input length. (따라서, 복잡도는 입력의 크기/길이에 대한 함수로 표현한다. ) This function usually gives the complexity for the worstcase input of any given length. (복잡도를 나타내는 함수는 통상 입력 크기가 최악인 경우를 고려한다. ) Page 51 Discrete Mathematics by Yang-Sae Moon

Example: Max Algorithm Complexity procedure max(a 1, a 2, …, an: integers) v : = a 1 {largest element so far} for i : = 2 to n {go thru rest of elems} if ai > v then v : = ai {found bigger? } {at this point v’s value is the same as the largest integer in the list} return v Problem: Find the exact order of growth ( ) of the worstcase time complexity of the max algorithm. Assume that each line of code takes some constant time every time it is executed. Page 52 Discrete Mathematics by Yang-Sae Moon

Complexity Analysis of Max Algorithm (1/2) Algorithm Complexity procedure max(a 1, a 2, …, an: integers) v : = a 1 t 1 for i : = 2 to n t 2 if ai > v then v : = ai return v t 3 t 4 Times for each execution of each line. (각 line을 하나의 수행으로 볼 때의 시간) What’s an expression for the exact total worst-case time? (Not its order of growth. ) (최악의 경우, 정확한 수행 시간을 어떻게 될까? ) Page 53 Discrete Mathematics by Yang-Sae Moon

Complexity Analysis of Max Algorithm (2/2) Algorithm Complexity procedure max(a 1, a 2, …, an: integers) v : = a 1 t 1 for i : = 2 to n t 2 if ai > v then v : = ai t 3 return v t 4 Times for each execution of each line. (각 line을 하나의 수행으로 볼 때의 시간) Worst case execution time: Page 54 Discrete Mathematics by Yang-Sae Moon

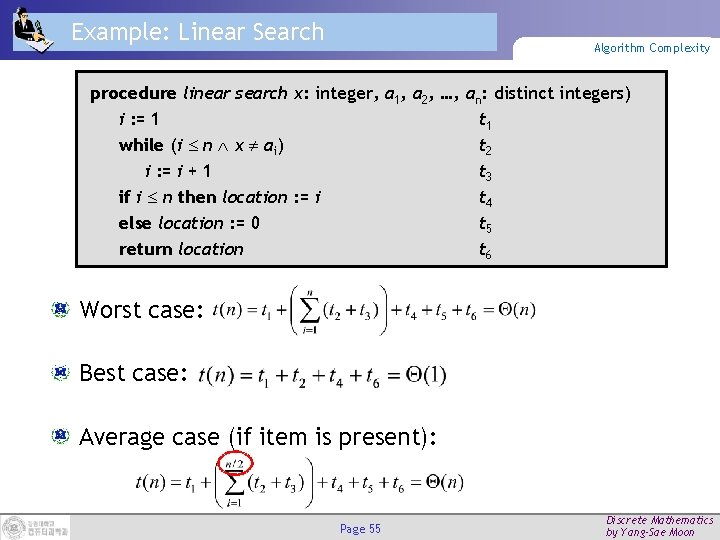
Example: Linear Search Algorithm Complexity procedure linear search x: integer, a 1, a 2, …, an: distinct integers) i : = 1 t 1 while (i n x ai) t 2 i : = i + 1 t 3 if i n then location : = i t 4 else location : = 0 t 5 return location t 6 Worst case: Best case: Average case (if item is present): Page 55 Discrete Mathematics by Yang-Sae Moon

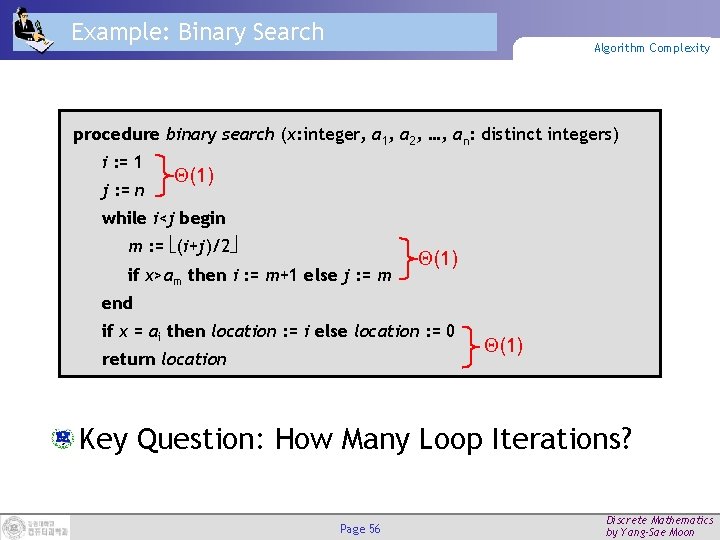
Example: Binary Search Algorithm Complexity procedure binary search (x: integer, a 1, a 2, …, an: distinct integers) i : = 1 j : = n (1) while i<j begin m : = (i+j)/2 if x>am then i : = m+1 else j : = m (1) end if x = ai then location : = i else location : = 0 return location (1) Key Question: How Many Loop Iterations? Page 56 Discrete Mathematics by Yang-Sae Moon

Binary Search Analysis Algorithm Complexity Suppose n=2 k. Original range from i=1 to j=n contains n elements. Each iteration: Size j i+1 of range is cut in half. (매번 검색 범위(j-i+1)의 절반(½)씩 줄여 나간다. ) Loop terminates when size of range is 1=20 (i=j). (검색 범위의 변화: 2 k 2 k-1 2 k-2 … 21 20, 결국 반복 횟수 = k) Therefore, number of iterations is k = log 2 n = (log 2 n)= (log n) (반복 횟수 = k이고, log 2 n = log 22 k이므로…) Even for n 2 k (not an integral power of 2), time complexity is still (log 2 n) = (log n). Page 57 Discrete Mathematics by Yang-Sae Moon

Example: Bubble Sort 1 st pass 3 2 4 1 5 2 3 4 1 5 3 rd pass 2 1 3 4 5 1 2 3 4 5 2 3 4 1 5 Algorithm Complexity 2 3 1 4 5 2 nd pass 2 3 1 4 5 4 th pass 1 2 3 4 5 2 3 1 4 5 2 1 3 4 5 Consider # of compare operations only! (n-1) + (n-2) + … + 2 + 1 = ((n-1)n)/2 = (n 2) Page 58 Discrete Mathematics by Yang-Sae Moon

Example: Insertion Sort 3 2 4 1 5 2 3 4 1 5 Algorithm Complexity 2 3 4 1 5 1 2 3 4 5 Also, consider # of compare operations only! 1 + 2 + … + (n-2) + (n-1) = ((n-1)n)/2 = (n 2) Then, are all sorting algorithm’s complexities (n 2)? NO! …, merge sort, heap sort, quick sort, … Page 59 Discrete Mathematics by Yang-Sae Moon

Names for Some Orders of Growth (1) Constant (log n) Logarithmic (n) Linear (n log n) Polylogarithmic (nc) Polynomial (cn), c>1 Exponential (n!) Factorial Page 60 Algorithm Complexity Discrete Mathematics by Yang-Sae Moon

Tractable versus Intractable Algorithm Complexity A problem or algorithm with at most polynomial time complexity is considered tractable (or feasible). P is the set of all tractable problems. (Polynomial 복잡도를 가지면, 풀만한(풀기 쉬운) 문제라 여기며, 이러한 문제들 의 집합을 P라 나타낸다. ) A problem or algorithm that has more than polynomial complexity is considered intractable (or infeasible). (Polynomial 복잡도 이상이면 풀기 어려운 문제라 여긴다. ) But, note that • n 1, 000 is technically tractable, but really impossible. • clog log n is technically intractable, but easy. Page 61 Discrete Mathematics by Yang-Sae Moon

Unsolvable Problems Algorithm Complexity Alan Turing discovered in the 1930’s that there are problems unsolvable by any algorithm. (튜링은 “어떠한 알고리즘으로도 풀 수 없는 문제가 있음”을 밝혔다. ) Example: the halting problem. • Given an arbitrary algorithm and its input, will that algorithm eventually halt, or will it continue forever in an “infinite loop? ” (주어진 알고리즘이 결국 정지하는지의 여부를 판단하는 문제는 결국 풀 수가 없다. ) Page 62 Discrete Mathematics by Yang-Sae Moon

P versus NP (1/3) Algorithm Complexity P is the set of all tractable problems. (i. e. , the problems have at most polynomial time complexity. ) (통상적으로 polynomial complexity를 가지면 P이다. ) NP is the set of problems for which there exists a tractable algorithm for checking solutions to see if they are correct. • In other words, NP is the set of decision problems for which a given proposed solution for a given input can be checked quickly (in polynomial time) to see if it really is a solution. • 주어진 입력에 대해 제시된 솔루션이 바른 해인지의 여부를 빠르게(polynomial time) 판단할 수 있는 알고리즘이 존재하는 문제들의 집합이 NP이다. • 통상적으로 exponential/factorial complexity를 가지면 NP이다. Page 63 Discrete Mathematics by Yang-Sae Moon

P versus NP (2/3) - skip Algorithm Complexity NP-complete is the term used to describe decision problems that are the hardest ones in NP in the sense that, if there were a polynomialbounded algorithm for an NP complete problem, then there would be a polynomial-bounded algorithm for each problem in NP. • NP중에서도 어려운 문제들이란 용어를 의미하며, 하나의 NP-complete 문제가 풀리면 (P가 되면), 관련된 수많은 모든 NP-complete 문제가 동시에 풀리게 된다. • 많은 학자들은 어려운 많은 문제들에 대해서 NP-complete임을 증명(특정 문제가 다른 NP-complete 문제로 해석(변경)될 수 있음을 보임)하였다. Page 64 Discrete Mathematics by Yang-Sae Moon

P versus NP (3/3) - skip Algorithm Complexity We know P NP, but the most famous unproven conjecture in computer science is that this inclusion is proper (i. e. , that P NP rather than P=NP). Whoever first proves it will be famous! Page 65 Discrete Mathematics by Yang-Sae Moon

Computer Time Examples #ops(n) log 2 n n n log 2 n n 2 2 n n=10 3. 3 ns 10 ns 33 ns 100 ns 1. 024 s n=106 19. 9 ns 1 ms 19. 9 ms 16 m 40 s 10301, 004. 5 Gyr n! 3. 63 ms Ouch! Algorithm Complexity Assume time = 1 ns (10 9 second) per operation You should carefully design algorithms and write programs! Page 66 Discrete Mathematics by Yang-Sae Moon

강의 내용 Algorithms and Complexity 알고리즘(Algorithms) 함수의 증가(Growth of Functions) 알고리즘 복잡도(Algorithm Complexity) Page 67 Discrete Mathematics by Yang-Sae Moon

Homework #3 Algorithms and Complexity Homework #3 & Programming Assignment #1 Page 68 Discrete Mathematics by Yang-Sae Moon