ALGORITHMIC SZ TRANSFORMATIONS FOR CONTINUOUSTIME TO DISCRETETIME FILTER

ALGORITHMIC S-Z TRANSFORMATIONS FOR CONTINUOUS-TIME TO DISCRETETIME FILTER CONVERSION D. Biolek, V. Biolkova Brno University of Technology Czech Republic http: //www. vabo. cz/stranky/biolek

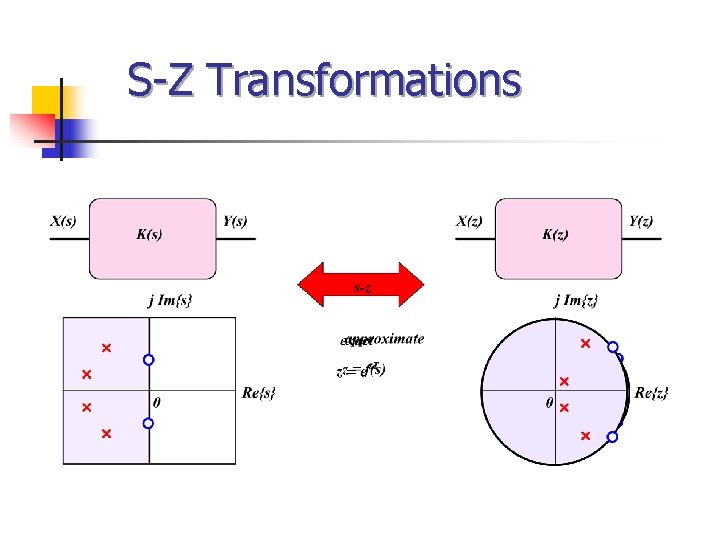
Introduction Generalized Pascal matrix: Using this matrix, the coefficients of transfer functions of the continuous -time and discrete-time linear circuits can be converted on the assumption that both circuits are related by a general first-order s-z transformation. Effective numerical procedure of computing all matrix elements for arbitrary first-order s-z transformation.

S-Z Transformations

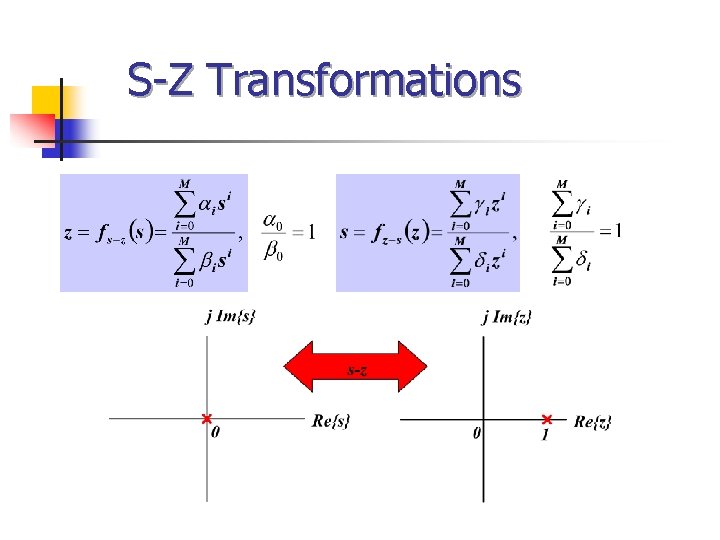
S-Z Transformations

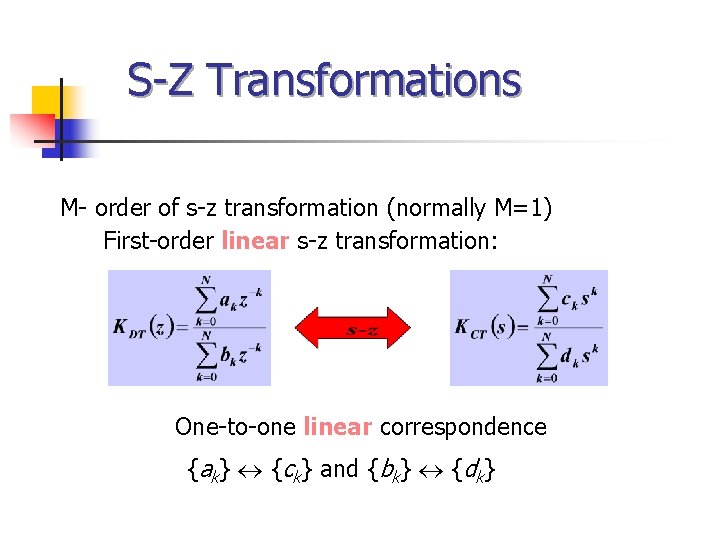
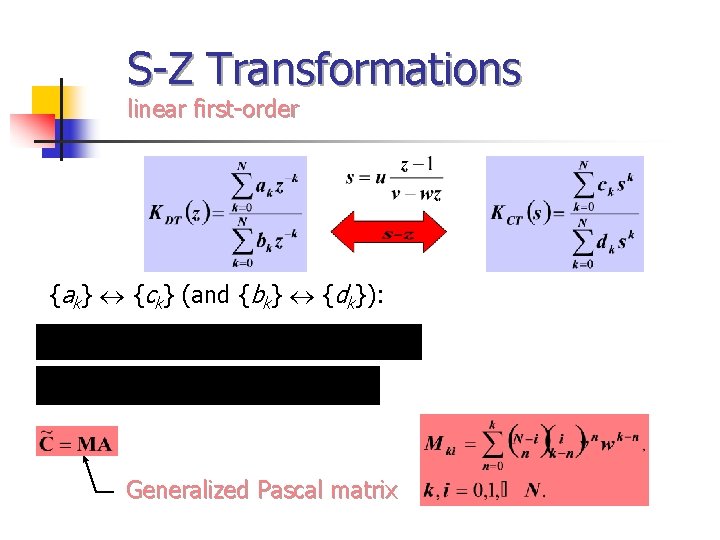
S-Z Transformations M- order of s-z transformation (normally M=1) First-order linear s-z transformation: One-to-one linear correspondence {ak} {ck} and {bk} {dk}

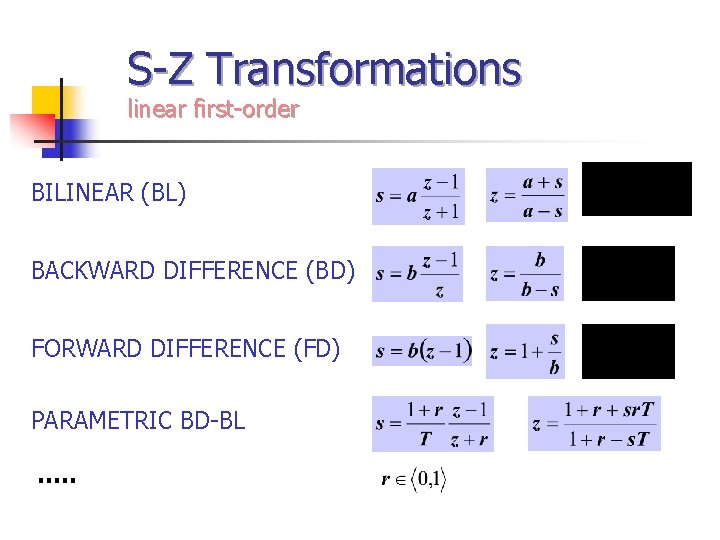
S-Z Transformations linear first-order BILINEAR (BL) BACKWARD DIFFERENCE (BD) FORWARD DIFFERENCE (FD) PARAMETRIC BD-BL …. .

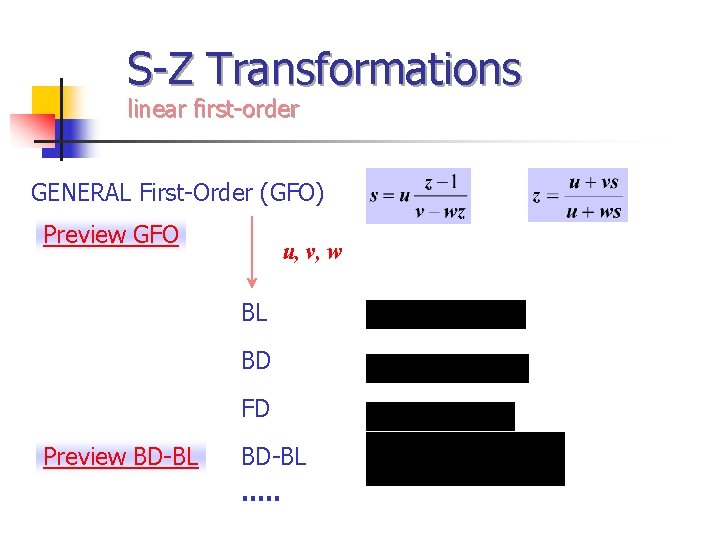
S-Z Transformations linear first-order GENERAL First-Order (GFO) Preview GFO u, v, w BL BD FD Preview BD-BL …. .

S-Z Transformations linear first-order {ak} {ck} (and {bk} {dk}): Generalized Pascal matrix

S-Z Transformations Generalized Pascal matrix (GPM)

S-Z Transformations Generalized Pascal matrix (GPM) Example: N=5 BL

S-Z Transformations Generalized Pascal matrix (GPM) Example: N=5 BD

S-Z Transformations Generalized Pascal matrix (GPM) Example: N=5 FD

S-Z Transformations Generalized Pascal matrix (GPM) Example: N=5 BD-BL

S-Z Transformations Algorithmic compilation of GPM … vector of DFT coefficients of i-th column of the GPM.

S-Z Transformations Algorithmic compilation of GPM 1. i = 0. 2. Compiling vectors ai and bi of a size 1 x (N+1) according to the rule 3. Completing both vectors by as much zeros as needed to reach their length to integer power of two. New vectors are obtained.

S-Z Transformations Algorithmic compilation of GPM 4. Performing FFT of vectors 5. Multiplying vectors above element per element and performing inverse FFT: 6. First N+1 elements give the i-th column of the GPM. 7. i = i+1; if i<=N then go to the step 2 else end.

S-Z Transformations Algorithmic compilation of GPM - example Example: Parametric BD-BL, r=0. 5, N=5. Calculation of GPM in MATLAB: 1. i = 0; 2. ai = [1 2. 5 1. 25 0. 3125 0. 03125]; bi = [1 0 0 0]; 3. = [1 2. 5 1. 25 0. 3125 0. 03125 0 0]; = [1 0 0 0 0];

S-Z Transformations Algorithmic compilation of GPM - example 4. 7. 59375 1. 54929 -5. 12955 i -1. 1875 -1. 28125 i -0. 17429 -0. 12955 i 0. 03125 0. 17429+0. 12955 i -1. 1875+1. 28125 i 1. 54929+5. 12955 i 1 1 1 1 5 -6. % i =0 1 2. 5 1. 25 0. 3125 0. 03125 0 0

Conclusions • The proposed algorithm generates all elements of GPM of arbitrary first-order s-z transformation. • The described approach is based on the FFT algorithm, which ensures the computation efficiency. • The structure of this procedure is not dependent on the type of s-z transformation.