Algorithmic Robotics and Molecular Modeling Dan Halperin School

Algorithmic Robotics and Molecular Modeling Dan Halperin School of Computer Science Tel Aviv University June 2007

Robotics RAS field of interest (ICRA, Rome, April 2007) : Robotics focuses on sensor and actuator systems that operate autonomously or semi-autonomously (in cooperation with humans) in unpredictable environments. Robot systems emphasize intelligence and adaptability, may be networked, and are being developed for many applications such as service and personal assistants; surgery and rehabilitation; haptics; space, underwater, and remote exploration and teleoperation; education, entertainment; search and rescue; defense; agriculture; and intelligent vehicles.

Algorithmic Robotics and Motion Planning [Latombe et al]

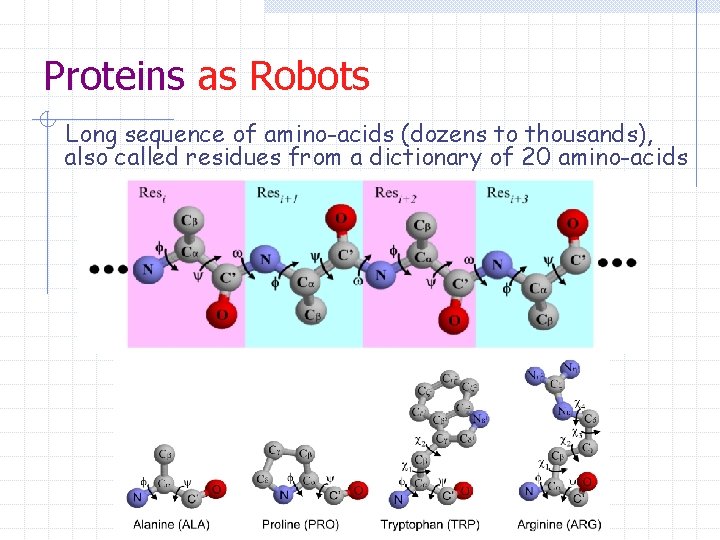
Proteins as Robots Long sequence of amino-acids (dozens to thousands), also called residues from a dictionary of 20 amino-acids

Robots with Many Dofs http: //www. youtube. com/watch? v=k-Vg. I 4 w. Ny. To

Simulation and Predicition of Molecular Motion [Enosh, Fleishman, Ben-Tal, H 2007] [Enosh-Raveh 2007]

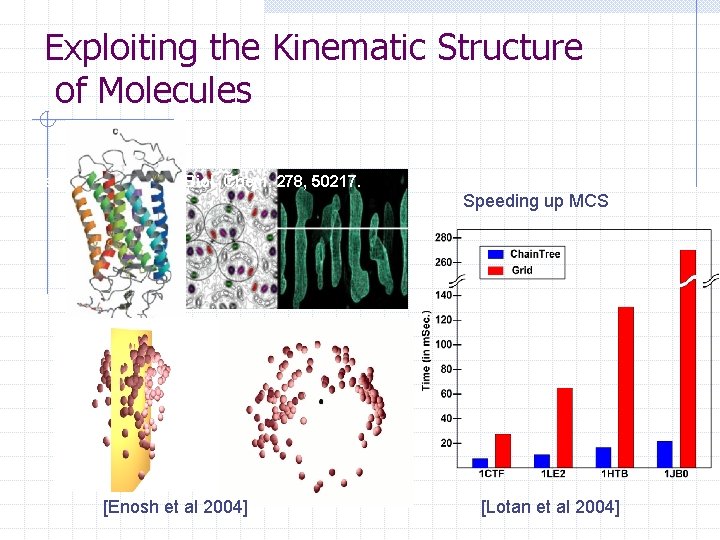
Exploiting the Kinematic Structure of Molecules Krebs et al. (2003) J. Biol. Chem. 278, 50217. Speeding up MCS [Enosh et al 2004] [Lotan et al 2004]

The Chain. Tree [Lotan, Schwarzer, H, Latombe 2004] TAI BAH TAE BAD TAC BAB TAB BA A TEI BEH TCE BCD TBC BB B TCD BC C TEG BEF TDE BD D TEF BE E TGI BGH TFG BF F TGH BG G THI BH H I

Molecular Simulations Monte Carlo Simulation (MCS) Popular method for sampling the conformation space of proteins: § Estimate thermodynamic quantities § Search for low-energy conformations and the folded structure

MCS: How it works 1. Propose random change in conformation 2. Compute energy E of new conformation 3. Accept with probability: Requires >>106 steps to sample adequately

Energy function § Bonded terms: § § § Bond lengths: Bond angles: Dihedral angles: § Non-bonded terms: § § § Van der Waals: Electrostatic: Heuristic

Pair-wise interactions § Cutoff distance (6 - 12Å) § Linear number of interactions contribute to energy (H-Overmars ’ 98) Challenge: Find all interacting pairs without enumerating all pairs

Related work § Computer Science § Biology § Bounding volume hierarchies § Neighbor lists for collision detection § § § Gotschalk et al. ’ 96 Larsen et al. ’ 00 Guibas et al. ’ 02 § Space partition methods for collision detection § § Faverjon ’ 84 Halperin & Overmars ’ 98 § Collisions detection for chains § § Halperin et al. ’ 97 Guibas et al. ’ 02 § § Verlet ’ 67 Brooks et al. ’ 83 § Grid § § § Quentrec & Brot ’ 73 Hockney et al. ’ 74 Van Gunsteren et al. ’ 84 § Neighbor lists + grid § § Yip & Elber ’ 89 Petrella ’ 02

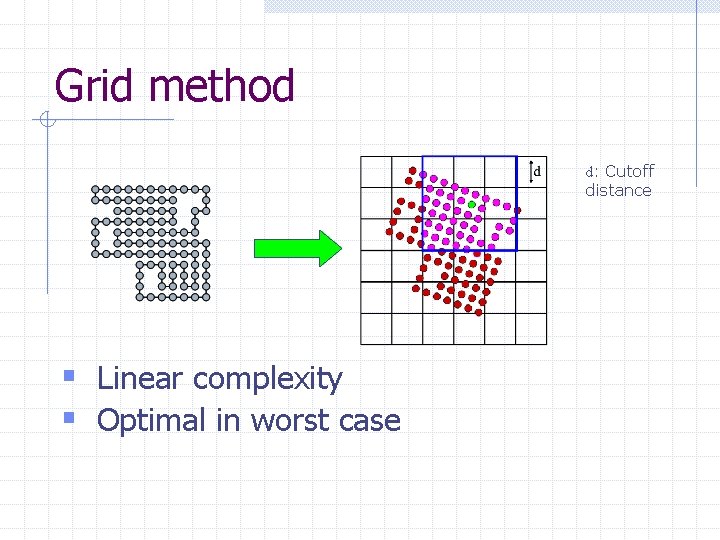
Grid method d: Cutoff distance § Linear complexity § Optimal in worst case

Contributions § Efficient maintenance and self-collision detection for kinematic chains § Efficient computation of pair-wise interactions in MCS of proteins § Scheme for caching and reusing partial energy sums during MCS § MCS software* Much faster than existing algorithm (grid method) *Download at: http: //robotics. stanford. edu/~itayl/mcs

Properties of kinematic chains § Small changes large effects

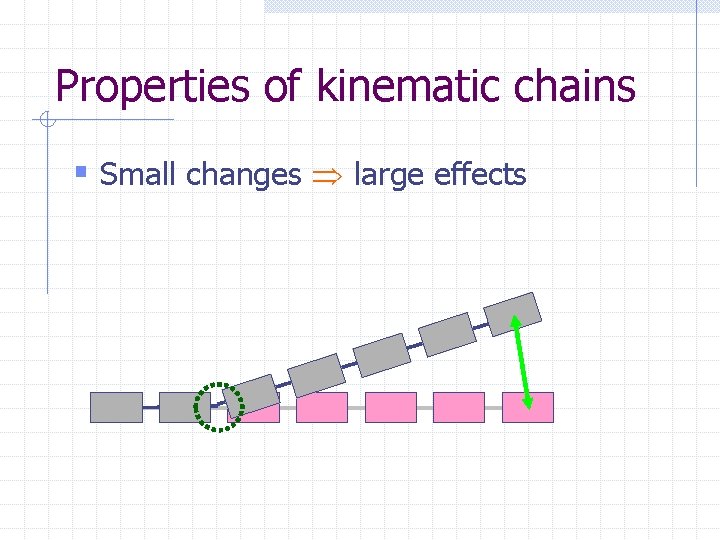
Properties of kinematic chains § Small changes large effects § Local changes global effects

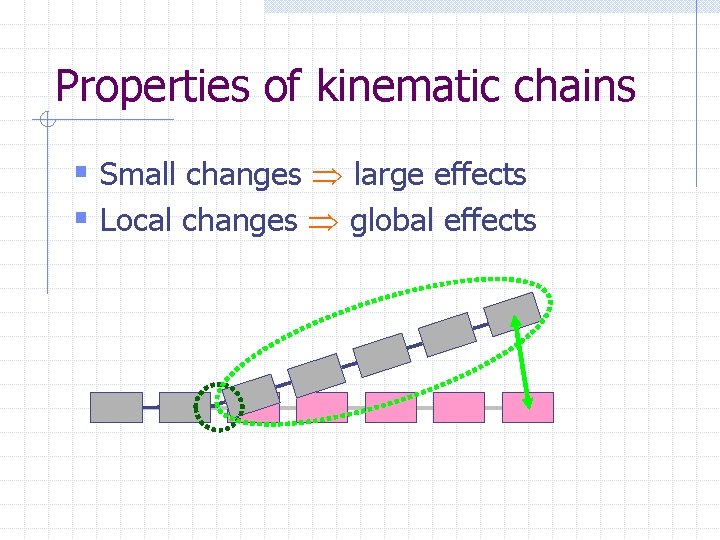
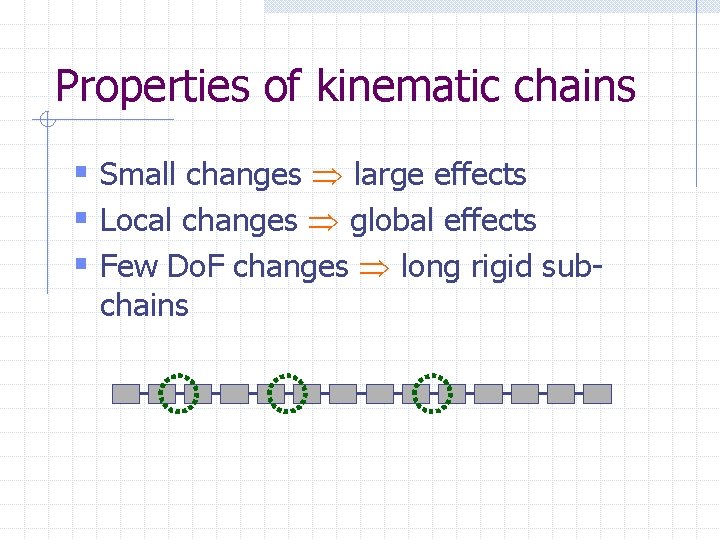
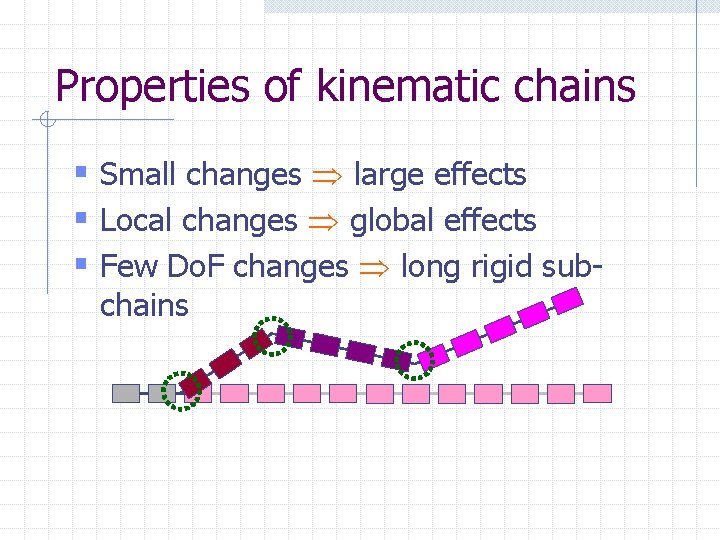
Properties of kinematic chains § Small changes large effects § Local changes global effects § Few Do. F changes long rigid subchains

Chain. Tree: A tale of two hierarchies § Transform hierarchy: approximates kinematics of protein backbone at successive resolutions § Bounding volume hierarchy: approximates geometry of protein at successive resolutions

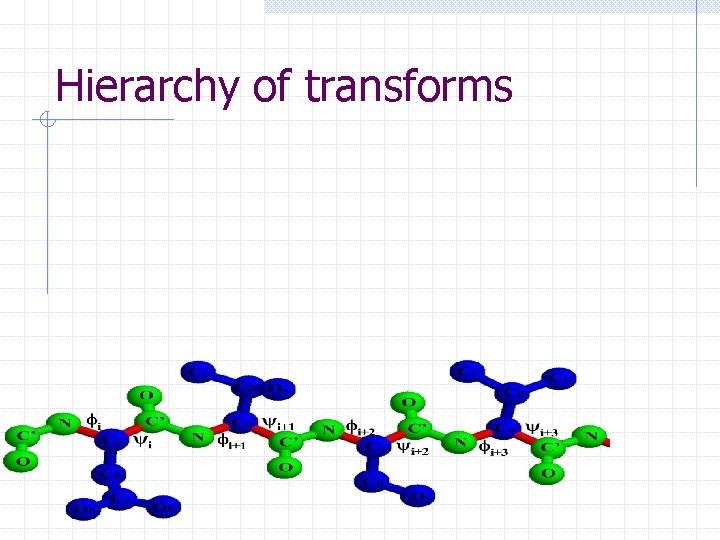
Hierarchy of transforms

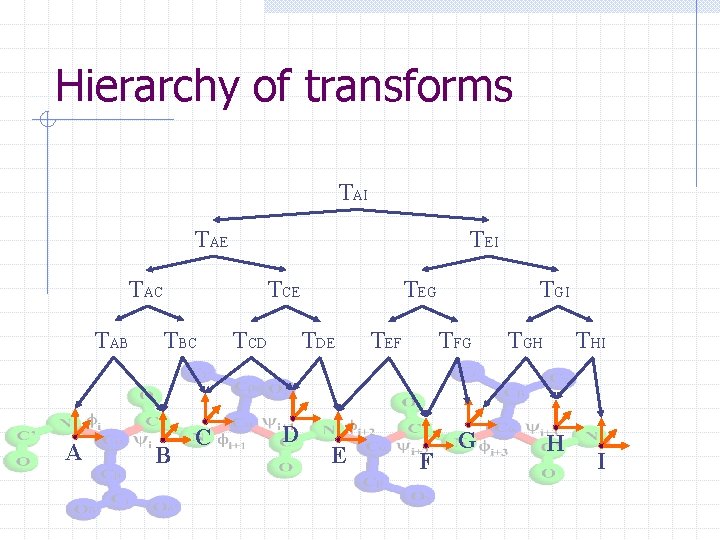
Hierarchy of transforms TAI TAE TEI TAC TAB A TCE TBC B C TCD TEG TDE D E TEF TGI TFG F G TGH THI H I

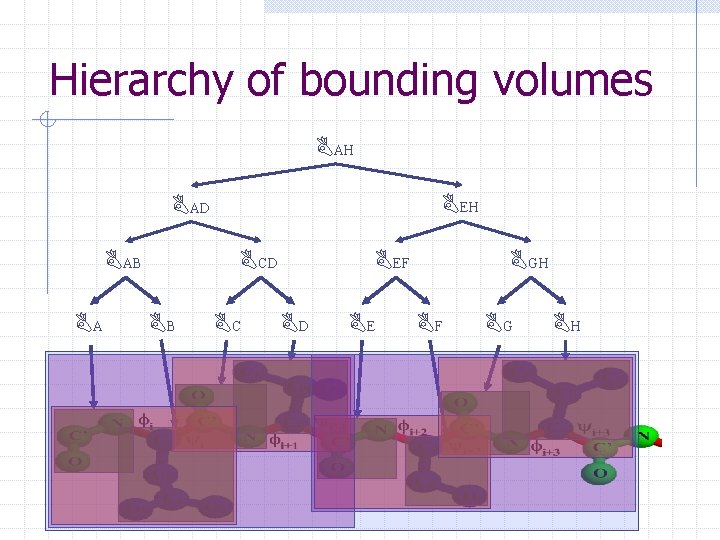
Hierarchy of bounding volumes BAH BEH BAD BCD BAB BA BB BC BEF BD BE BGH BF BG BH

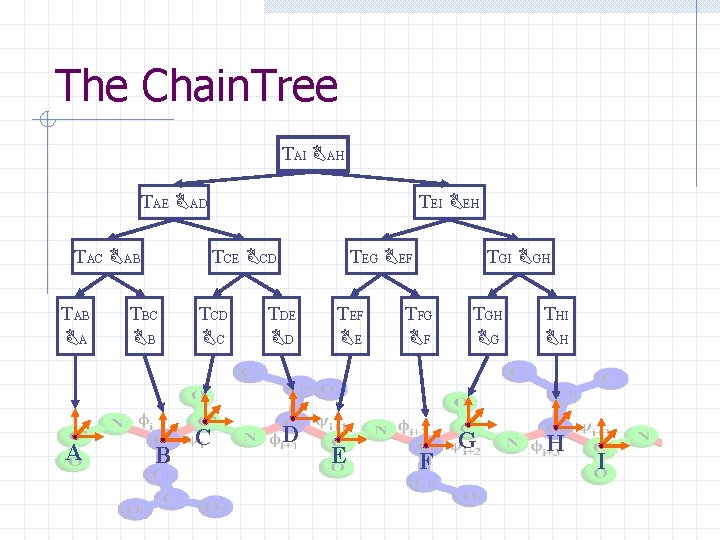
The Chain. Tree TAI BAH TAE BAD TAC BAB TAB BA A TEI BEH TCE BCD TBC BB B TCD BC C TEG BEF TDE BD D TEF BE E TGI BGH TFG BF F TGH BG G THI BH H I

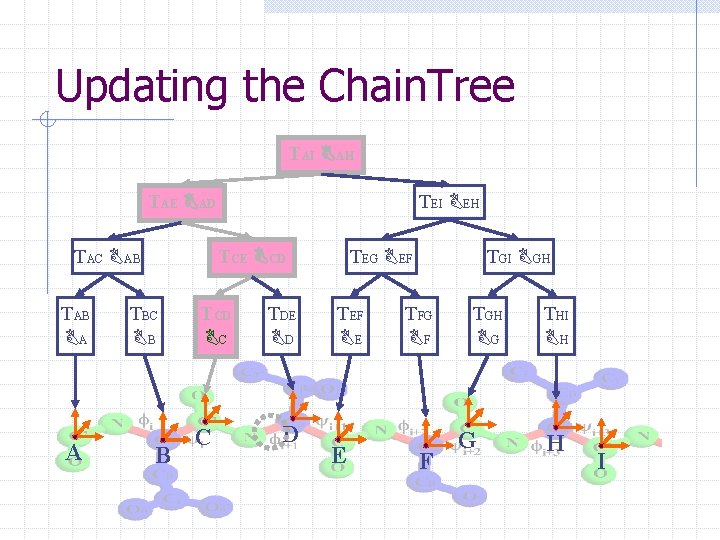
Updating the Chain. Tree TAI BAH TAE BAD TAC BAB TAB BA A TEI BEH TCE BCD TBC BB B TCD BC C TDE BD D TEG BEF TEF BE E TGI BGH TFG BF F TGH BG G THI BH H I

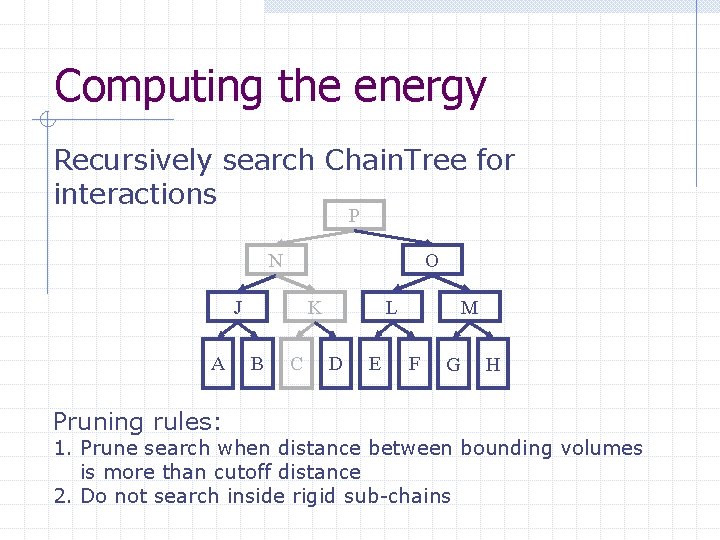
Computing the energy Recursively search Chain. Tree for interactions P N O J A Pruning rules: K B C L D E M F G H 1. Prune search when distance between bounding volumes is more than cutoff distance 2. Do not search inside rigid sub-chains

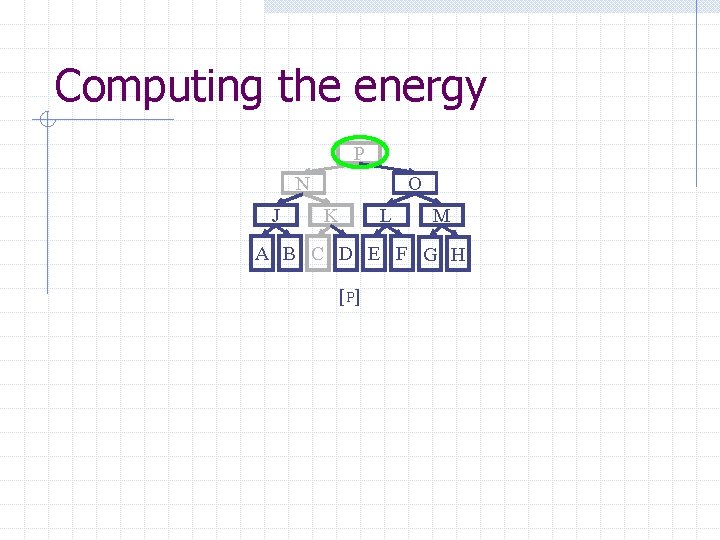
Computing the energy P N J O K L M A B C D E F G H [ P]

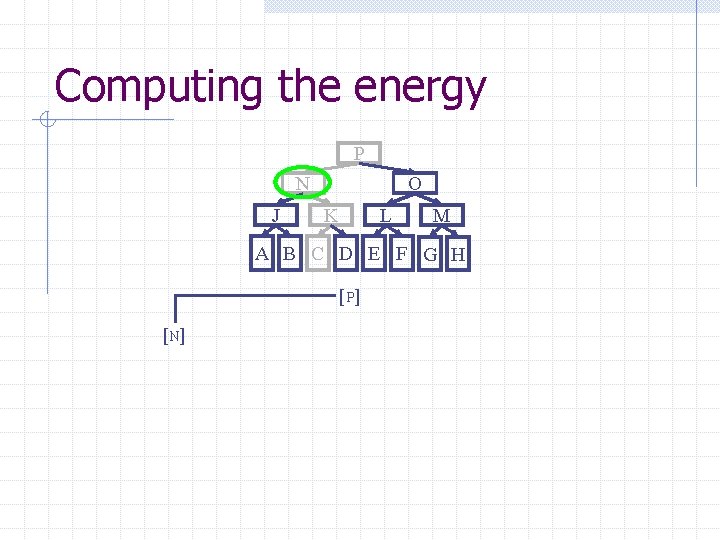
Computing the energy P N J O K L M A B C D E F G H [ P] [N]

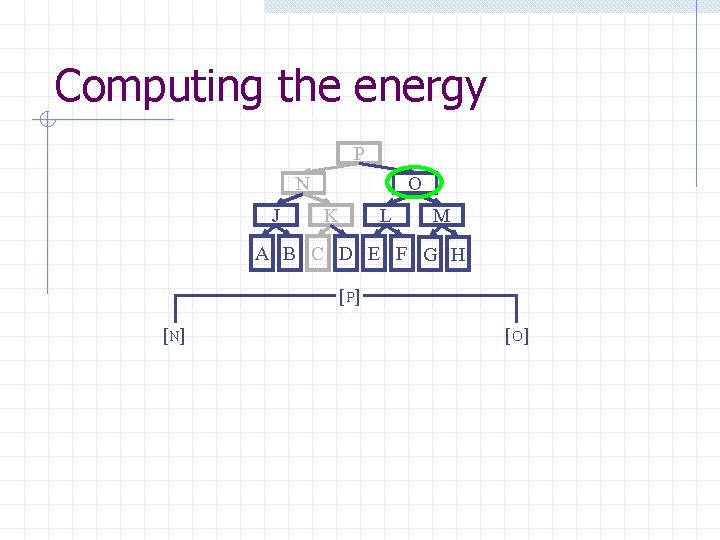
Computing the energy P N J O K L M A B C D E F G H [ P] [N] [O ]

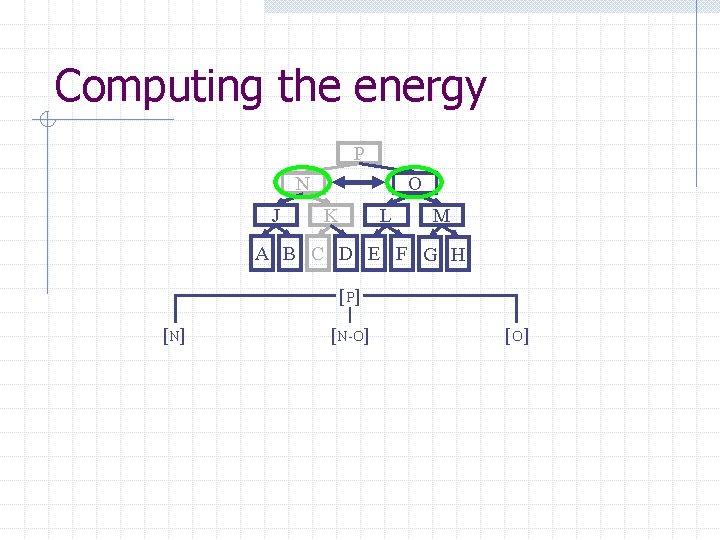
Computing the energy P N J O K L M A B C D E F G H [ P] [N-O] [O ]

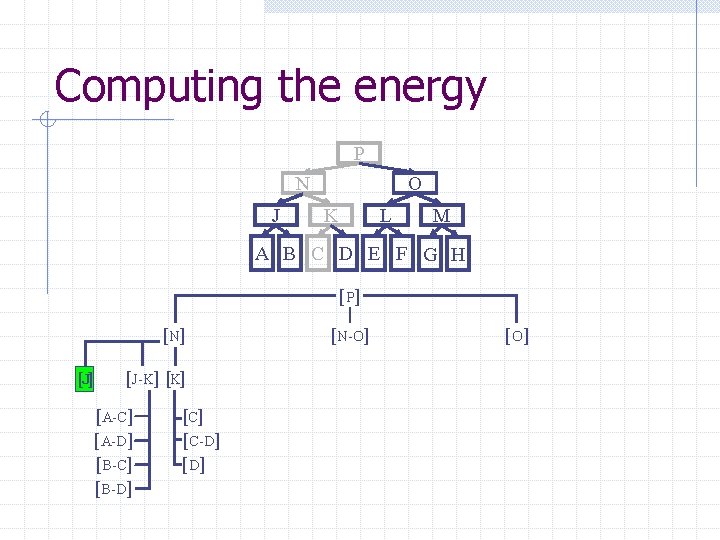
Computing the energy P N J O K L M A B C D E F G H [ P] [N] [J-K] [A-C] [A-D] [B-C] [B-D] [C-D] [N-O] [O ]

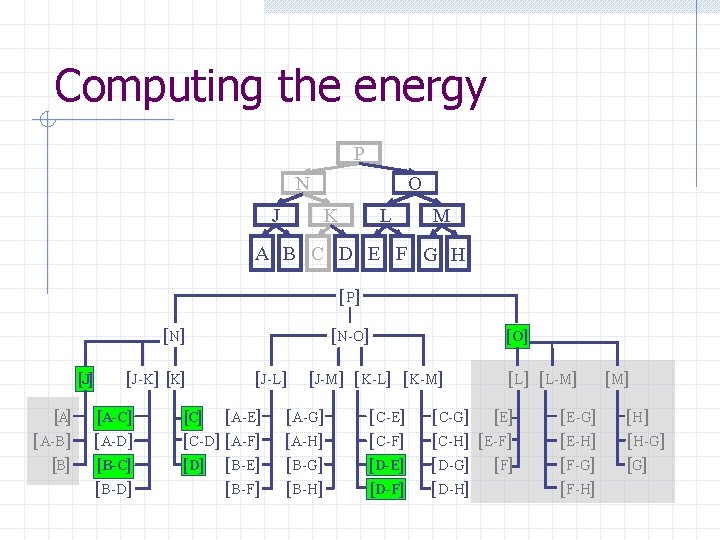
Computing the energy P N J O K L M A B C D E F G H [ P] [N] [J] [A-B] [J-K] [A-C] [A-D] [B-C] [B-D] [N-O] [J-L] [C] [A-E] [C-D] [A-F] [D] [B-E] [B-F] [O] [J-M] [K-L] [K-M] [A-G] [A-H] [B-G] [B-H] [C-E] [C-F] [D-E] [D-F] [L-M] [C-G] [E] [C-H] [E-F] [D-G] [F] [D-H] [E-G] [E-H] [F-G] [F-H] [M] [H-G] [G]

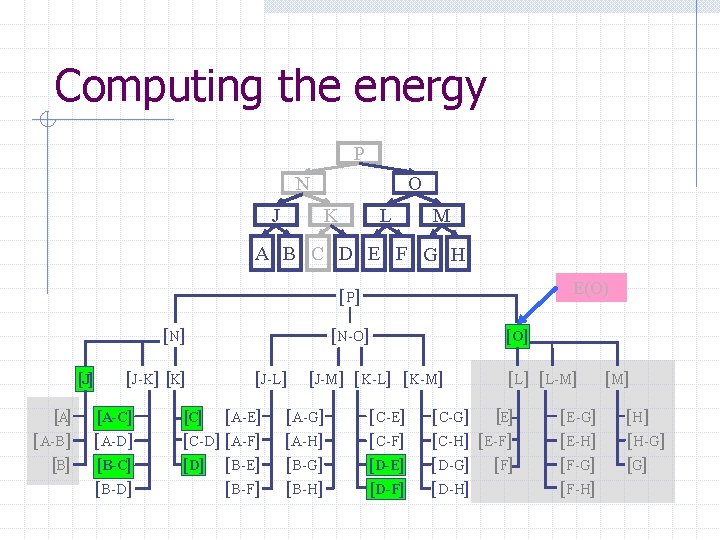
Computing the energy P N J O K L M A B C D E F G H E(O) [ P] [N] [J] [A-B] [J-K] [A-C] [A-D] [B-C] [B-D] [N-O] [J-L] [C] [A-E] [C-D] [A-F] [D] [B-E] [B-F] [O] [J-M] [K-L] [K-M] [A-G] [A-H] [B-G] [B-H] [C-E] [C-F] [D-E] [D-F] [L-M] [C-G] [E] [C-H] [E-F] [D-G] [F] [D-H] [E-G] [E-H] [F-G] [F-H] [M] [H-G] [G]

Computing the energy § Only changed interactions are found § Reuse unaffected partial sums § Better performance for § Longer proteins § Fewer simultaneous changes

Computational complexity § Updating: § Searching: worst case bound Much faster in practice

Test 1 -Do. F change [68 res. ] [144 res. ] [374 res. ] 5 -Do. F change [755 res. ] [68 res. ] [144 res. ] [374 res. ] [755 res. ]

Dynamic Maintenance of Molecular Surfaces [Eyal-H 2005]

Major Goals § Dynamic maintenance of molecular properties in MD-type simulations § Simulation and prediction of motion with more dofs § Fast and accurate IK (loop closure)

THE END