Algorithmen und Datenstrukturen Prof Dr Ralf Mller Universitt



![DFS-Nummerierung Variablen: • dfs. Num: Array [1. . n] of ℕ • finish. Time: DFS-Nummerierung Variablen: • dfs. Num: Array [1. . n] of ℕ • finish. Time:](https://slidetodoc.com/presentation_image/4c16c3f15c6a1724eb17812e83cf8562/image-6.jpg)
![DFS-Nummerierung Ordnung < auf den Knoten: u<v gdw. dfs. Num[u]<dfs. Num[v] Lemma 1: Die DFS-Nummerierung Ordnung < auf den Knoten: u<v gdw. dfs. Num[u]<dfs. Num[v] Lemma 1: Die](https://slidetodoc.com/presentation_image/4c16c3f15c6a1724eb17812e83cf8562/image-8.jpg)

![DFS-Nummerierung Beobachtung für Kante (v, w): Kantentyp dfs. Num[v]< dfs. Num[w] finish. Time[v]> finish. DFS-Nummerierung Beobachtung für Kante (v, w): Kantentyp dfs. Num[v]< dfs. Num[w] finish. Time[v]> finish.](https://slidetodoc.com/presentation_image/4c16c3f15c6a1724eb17812e83cf8562/image-11.jpg)






![Starke ZHKs init(): component: Array [1. . n] of Node. Id o. Reps = Starke ZHKs init(): component: Array [1. . n] of Node. Id o. Reps =](https://slidetodoc.com/presentation_image/4c16c3f15c6a1724eb17812e83cf8562/image-38.jpg)


- Slides: 41

Algorithmen und Datenstrukturen Prof. Dr. Ralf Möller Universität zu Lübeck Institut für Informationssysteme Felix Kuhr (Übungen) sowie viele Tutoren

Danksagung Die nachfolgenden Präsentationen wurden mit ausdrücklicher Erlaubnis des Autors übernommen aus: • „Effiziente Algorithmen und Datenstrukturen“ (Kapitel 7, 8, 9) gehalten von Christian Scheideler an der TUM http: //www 14. in. tum. de/lehre/2008 WS/ea/index. html. de Es wurden umfangreiche Veränderungen vorgenommen Fehler sind selbstverständlich uns zuzuschreiben 2

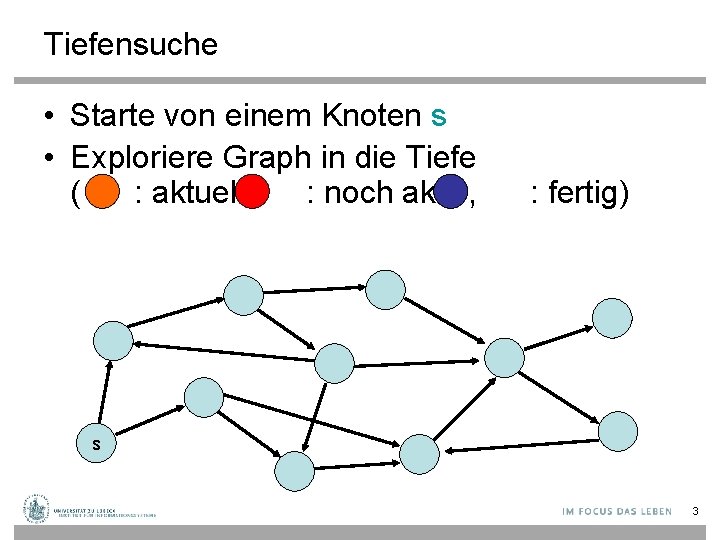
Tiefensuche • Starte von einem Knoten s • Exploriere Graph in die Tiefe ( : aktuell, : noch aktiv, : fertig) s 3

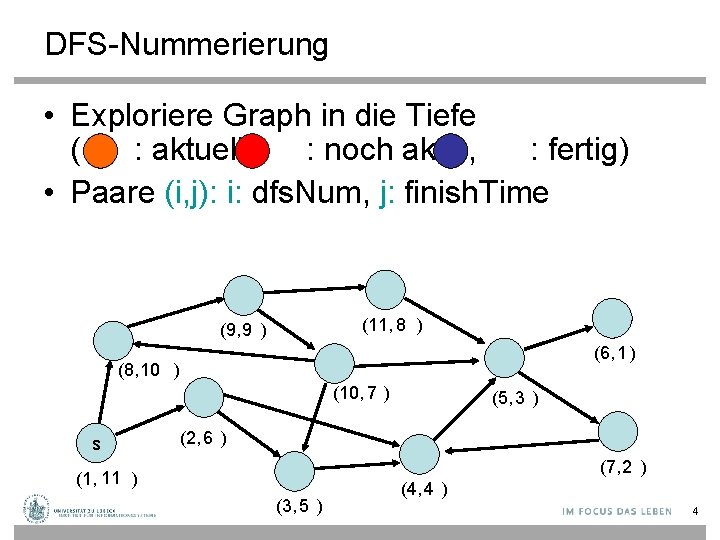
DFS-Nummerierung • Exploriere Graph in die Tiefe ( : aktuell, : noch aktiv, : fertig) • Paare (i, j): i: dfs. Num, j: finish. Time (11, 8 ) (9, 9 ) (6, 1 ) (8, 10 ) (10, 7 ) s (5, 3 ) (2, 6 ) (7, 2 ) (1, 11 ) (3, 5 ) (4, 4 ) 4

Tiefensuche – Design Pattern Übergeordnete Prozedur: unmark all nodes init() for s∈V do // stelle sicher, dass alle Knoten besucht werden if s is not marked then mark s root(s) DFS(s, s) // s: Startknoten Procedure DFS(u, v: Node) // u: Vater von v for (v, w)∈E do if w is marked then handle. Non. Tree. Edge(v, w) else traverse. Tree. Edge(v, w) mark w DFS(v, w) Könnte man das backtrack(u, v) auch iterativ lösen? Prozeduren in rot: noch zu spezifizieren 5
![DFSNummerierung Variablen dfs Num Array 1 n of ℕ finish Time DFS-Nummerierung Variablen: • dfs. Num: Array [1. . n] of ℕ • finish. Time:](https://slidetodoc.com/presentation_image/4c16c3f15c6a1724eb17812e83cf8562/image-6.jpg)
DFS-Nummerierung Variablen: • dfs. Num: Array [1. . n] of ℕ • finish. Time: Array [1. . n] of ℕ • dfs. Pos, finishing. Time: ℕ // Zeitpunkt wenn Knoten // Zähler � Code-Stücke: • init(): dfs. Pos: =1; finishing. Time: =1 • root(s): dfs. Num[s]: =dfs. Pos; dfs. Pos: =dfs. Pos+1 • traverse. Tree. Edge(v, w): dfs. Num[w]: =dfs. Pos; dfs. Pos: =dfs. Pos+1 • handle. Non. Tree. Edge(v, w): • backtrack(u, v): finish. Time[v]: =finishing. Time; finishing. Time : = finishing. Time+1 6

DFS-Nummerierung • Exploriere Graph in die Tiefe ( : aktuell, : noch aktiv, : fertig) • Paare (i, j): i: dfs. Num, j: finish. Time • DFS-Nummerierung in O(n+m) (11, 8 ) (9, 9 ) (6, 1 ) (8, 10 ) (10, 7 ) s (5, 3 ) (2, 6 ) (7, 2 ) (1, 11 ) (3, 5 ) (4, 4 ) 7
![DFSNummerierung Ordnung auf den Knoten uv gdw dfs Numudfs Numv Lemma 1 Die DFS-Nummerierung Ordnung < auf den Knoten: u<v gdw. dfs. Num[u]<dfs. Num[v] Lemma 1: Die](https://slidetodoc.com/presentation_image/4c16c3f15c6a1724eb17812e83cf8562/image-8.jpg)
DFS-Nummerierung Ordnung < auf den Knoten: u<v gdw. dfs. Num[u]<dfs. Num[v] Lemma 1: Die Knoten im DFS-Rekursionsstack (alle Knoten) sind sortiert bezüglich <. Beweis: dfs. Pos wird nach jeder Zuweisung von dfs. Num erhöht. Jeder neue aktive Knoten hat also immer die höchste dfs. Num. 8

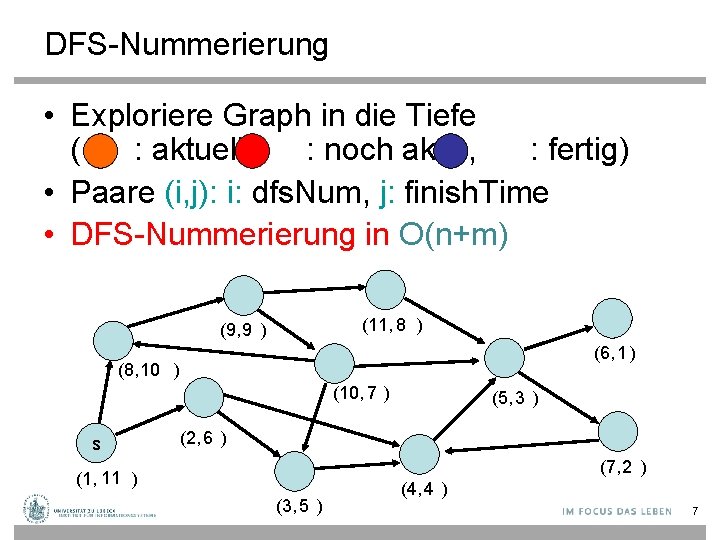
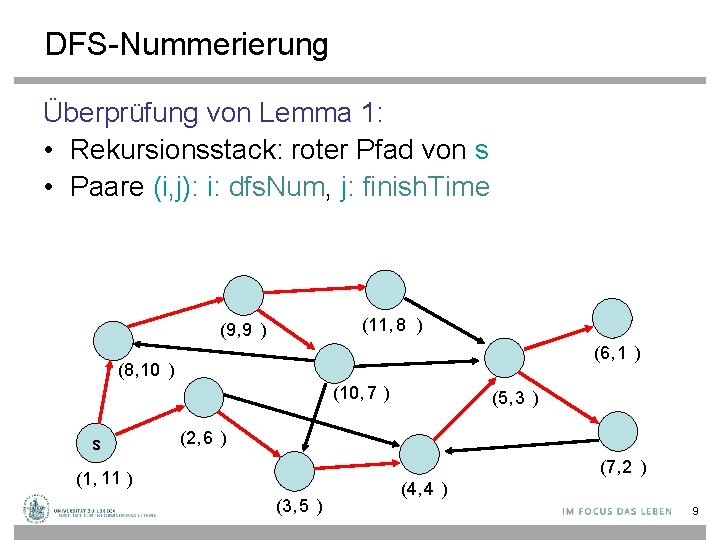
DFS-Nummerierung Überprüfung von Lemma 1: • Rekursionsstack: roter Pfad von s • Paare (i, j): i: dfs. Num, j: finish. Time (11, 8 ) (9, 9 ) (6, 1 ) (8, 10 ) (10, 7 ) s (5, 3 ) (2, 6 ) (7, 2 ) (1, 11 ) (3, 5 ) (4, 4 ) 9

DFS-Nummerierung • Baumkante: zum Kind • Vorwärtskante: zu einem Nachkommen • Rückwärtskante: zu einem Vorfahr (siehe handle. Non. Tree. Edge) • Kreuzkante: alle sonstige Kanten (siehe handle. Non. Tree. Edge) (11, 8 ) (9, 9 ) (6, 1 ) (8, 10 ) (10, 7 ) s (5, 3 ) (2, 6 ) (7, 2 ) (1, 11 ) (3, 5 ) (4, 4 ) 10
![DFSNummerierung Beobachtung für Kante v w Kantentyp dfs Numv dfs Numw finish Timev finish DFS-Nummerierung Beobachtung für Kante (v, w): Kantentyp dfs. Num[v]< dfs. Num[w] finish. Time[v]> finish.](https://slidetodoc.com/presentation_image/4c16c3f15c6a1724eb17812e83cf8562/image-11.jpg)
DFS-Nummerierung Beobachtung für Kante (v, w): Kantentyp dfs. Num[v]< dfs. Num[w] finish. Time[v]> finish. Time[w] Baum & Vorwärts Ja Ja Rückwärts Nein Kreuz Nein Ja (11, 8 ) (9, 9 ) (6, 1 ) (8, 10 ) (10, 7 ) s (5, 3 ) (2, 6 ) (7, 2 ) (1, 11 ) (3, 5 ) (4, 4 ) 11

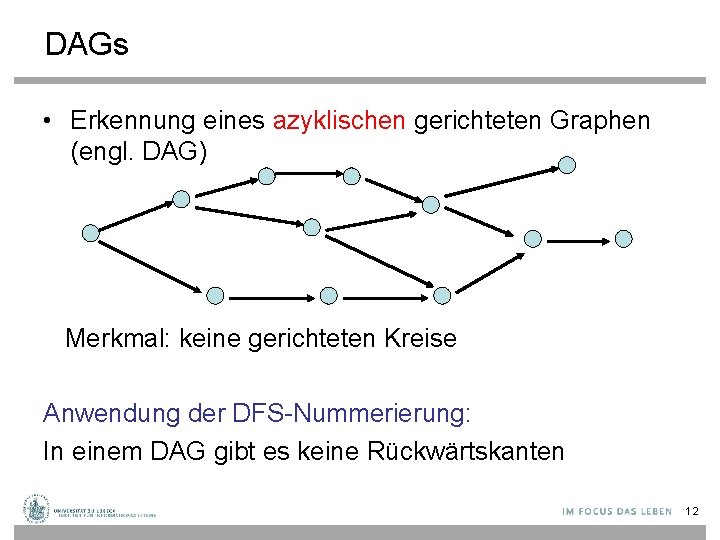
DAGs • Erkennung eines azyklischen gerichteten Graphen (engl. DAG) Merkmal: keine gerichteten Kreise Anwendung der DFS-Nummerierung: In einem DAG gibt es keine Rückwärtskanten 12

DFS-Nummerierung Behauptung: Folgende Aussagen sind äquivalent: 1. G ist ein DAG 2. DFS enthält keine Rückwärtskante 3. ∀(v, w)∈E : finish. Time[v]>finish. Time[w] Beweis ( 2. ⇔ 3. ): 2. ⇔ 3. : folgt aus Tabelle Kantentyp dfs. Num[v]< dfs. Num[w] finish. Time[v]> finish. Time[w] Baum & Vorwärts Ja Ja Rückwärts Nein Kreuz Nein Ja 13

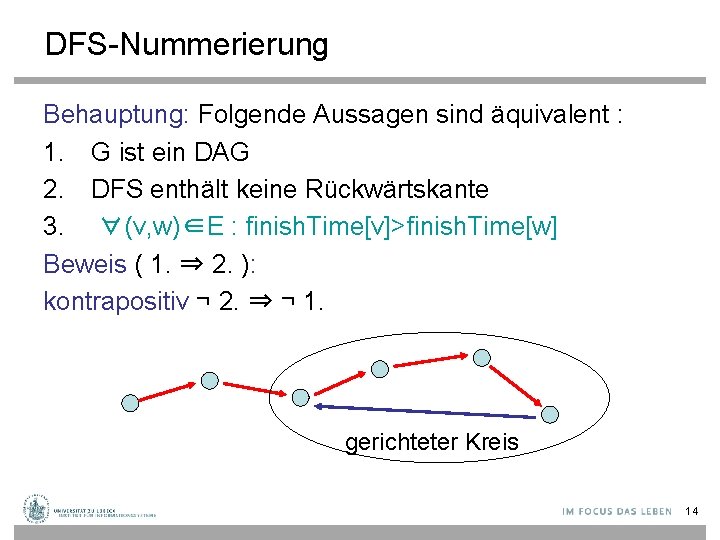
DFS-Nummerierung Behauptung: Folgende Aussagen sind äquivalent : 1. G ist ein DAG 2. DFS enthält keine Rückwärtskante 3. ∀(v, w)∈E : finish. Time[v]>finish. Time[w] Beweis ( 1. ⇒ 2. ): kontrapositiv ¬ 2. ⇒ ¬ 1. gerichteter Kreis 14

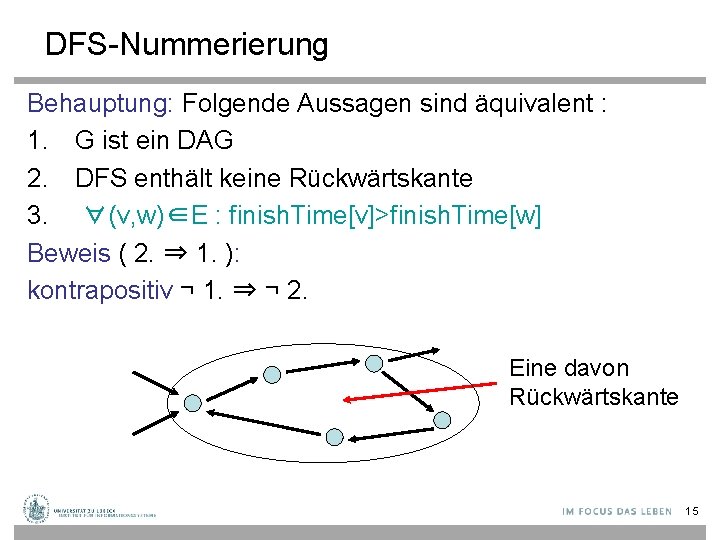
DFS-Nummerierung Behauptung: Folgende Aussagen sind äquivalent : 1. G ist ein DAG 2. DFS enthält keine Rückwärtskante 3. ∀(v, w)∈E : finish. Time[v]>finish. Time[w] Beweis ( 2. ⇒ 1. ): kontrapositiv ¬ 1. ⇒ ¬ 2. Eine davon Rückwärtskante 15

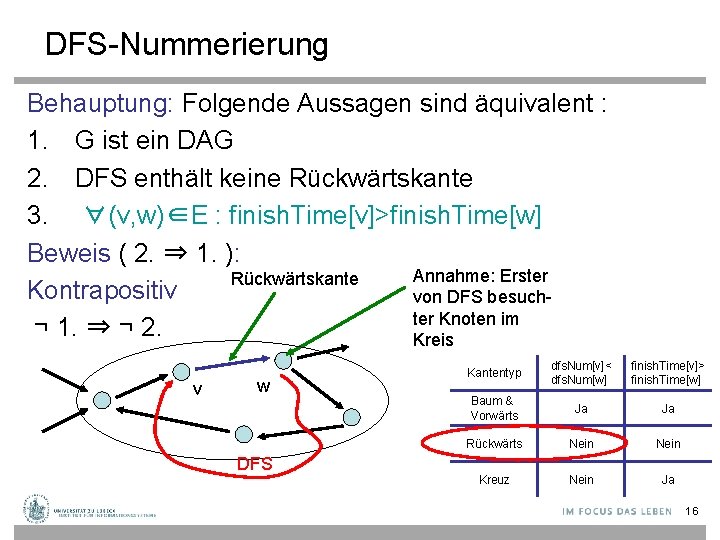
DFS-Nummerierung Behauptung: Folgende Aussagen sind äquivalent : 1. G ist ein DAG 2. DFS enthält keine Rückwärtskante 3. ∀(v, w)∈E : finish. Time[v]>finish. Time[w] Beweis ( 2. ⇒ 1. ): Annahme: Erster Rückwärtskante Kontrapositiv von DFS besuchter Knoten im ¬ 1. ⇒ ¬ 2. Kreis v w DFS Kantentyp dfs. Num[v]< dfs. Num[w] finish. Time[v]> finish. Time[w] Baum & Vorwärts Ja Ja Rückwärts Nein Kreuz Nein Ja 16

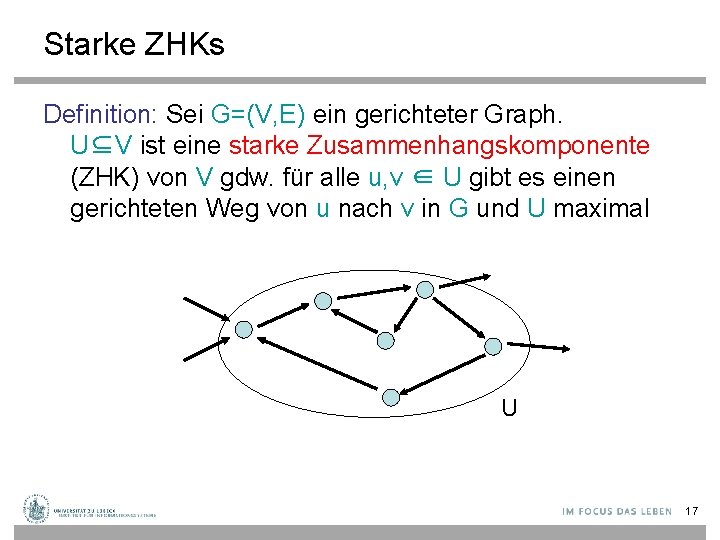
Starke ZHKs Definition: Sei G=(V, E) ein gerichteter Graph. U⊆V ist eine starke Zusammenhangskomponente (ZHK) von V gdw. für alle u, v ∈ U gibt es einen gerichteten Weg von u nach v in G und U maximal U 17

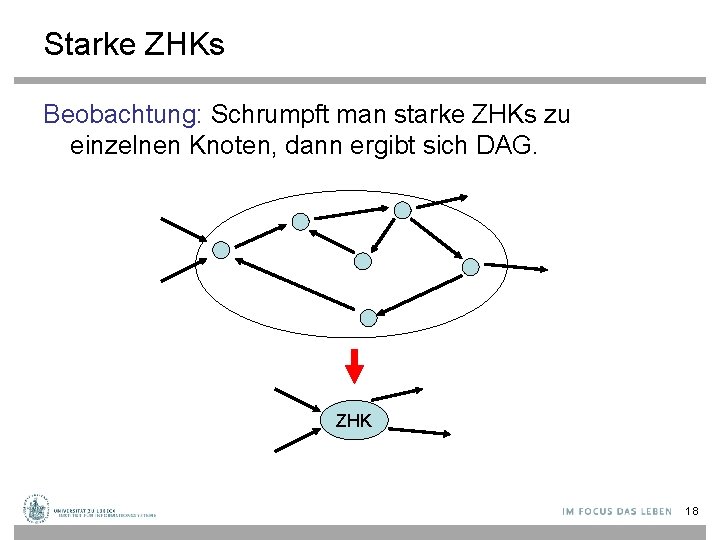
Starke ZHKs Beobachtung: Schrumpft man starke ZHKs zu einzelnen Knoten, dann ergibt sich DAG. ZHK 18

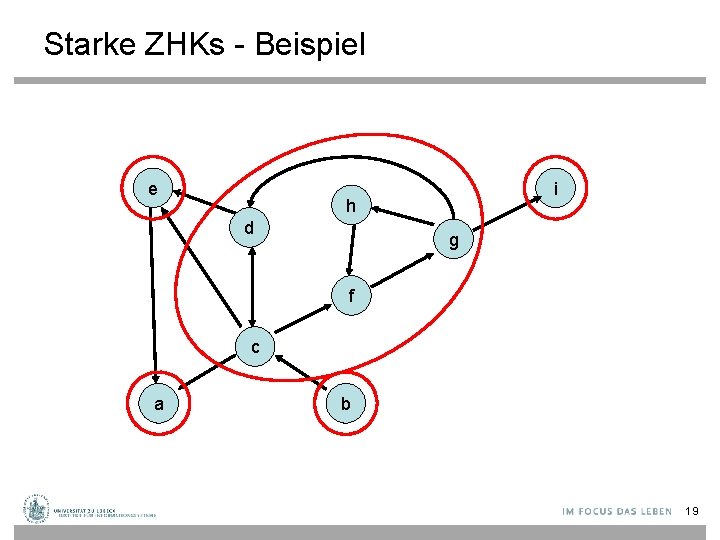
Starke ZHKs - Beispiel e i h d g f c a b 19

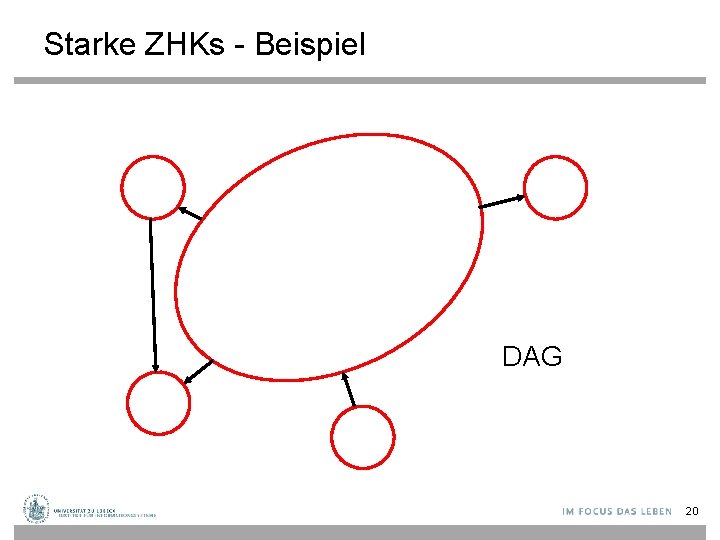
Starke ZHKs - Beispiel DAG 20

Starke ZHKs Ziel: Finde alle starken ZHKs im Graphen in O(n+m) Zeit (n: #Knoten, m: #Kanten) Strategie: Verwende DFS-Verfahren mit component: Array [1. . n] of 1. . n Am Ende: component[v]=component[w] ⇔ v und w sind in derselben starken ZHK Robert Tarjan: Depth-first search and linear graph algorithms. In: SIAM Journal on Computing. Bd. 1, Nr. 2, S. 146 -160, 1972 21

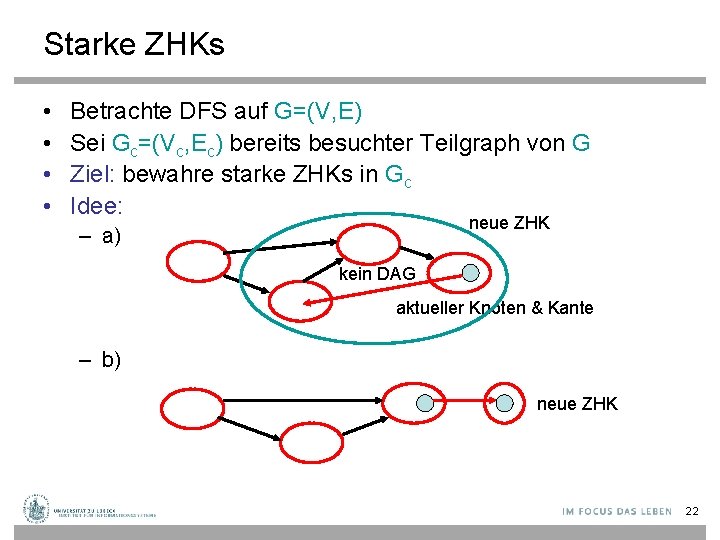
Starke ZHKs • • Betrachte DFS auf G=(V, E) Sei Gc=(Vc, Ec) bereits besuchter Teilgraph von G Ziel: bewahre starke ZHKs in Gc Idee: neue ZHK – a) kein DAG aktueller Knoten & Kante – b) neue ZHK 22

Starke ZHKs Warum ZHKs zu einer zusammenfassbar? neue ZHK kein DAG aktueller Knoten & Kante Grund: ZHK v ZHK für alle v, w: Weg von v nach w und umgekehrt ZHK w 23

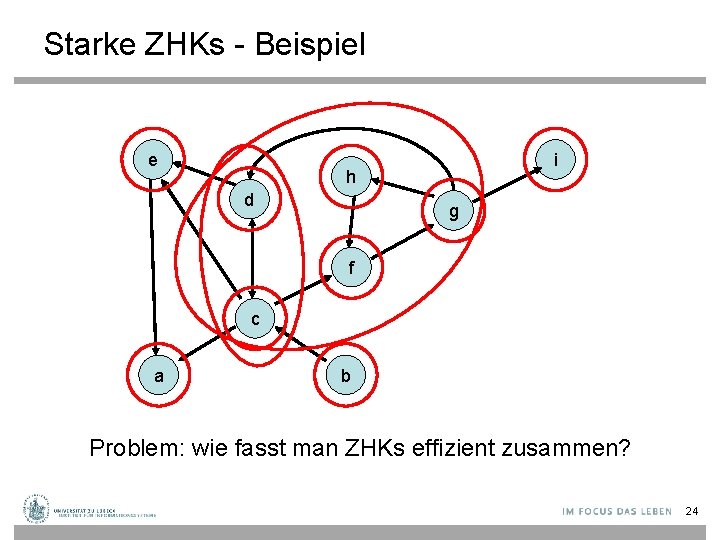
Starke ZHKs - Beispiel e i h d g f c a b Problem: wie fasst man ZHKs effizient zusammen? 24

Starke ZHKs Definition: • : unfertiger Knoten • : fertiger Knoten • Eine ZHK in G heißt offen, falls sie noch unfertige Knoten enthält. Sonst heißt sie (und ihre Knoten) geschlossen. • Repräsentant einer ZHK: Knoten mit kleinster dfs. Num. 25

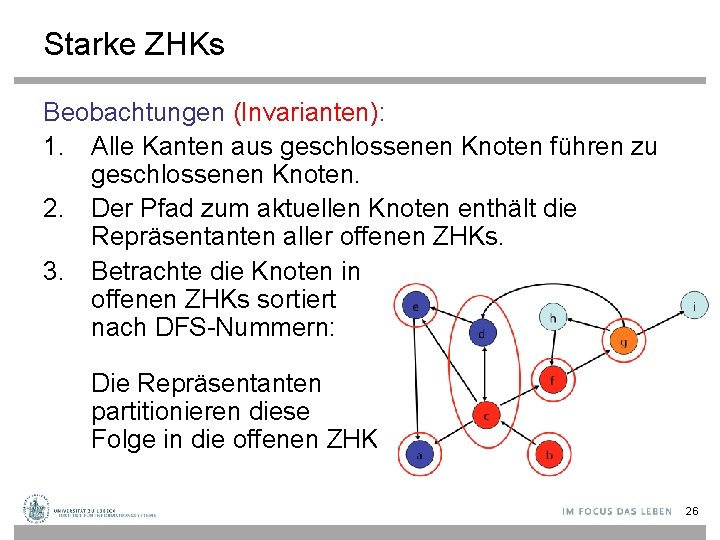
Starke ZHKs Beobachtungen (Invarianten): 1. Alle Kanten aus geschlossenen Knoten führen zu geschlossenen Knoten. 2. Der Pfad zum aktuellen Knoten enthält die Repräsentanten aller offenen ZHKs. 3. Betrachte die Knoten in offenen ZHKs sortiert nach DFS-Nummern: Die Repräsentanten partitionieren diese Folge in die offenen ZHKs. 26

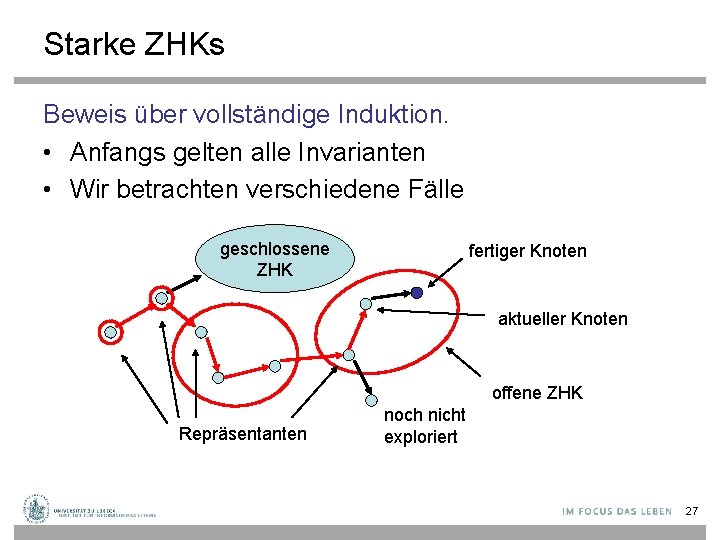
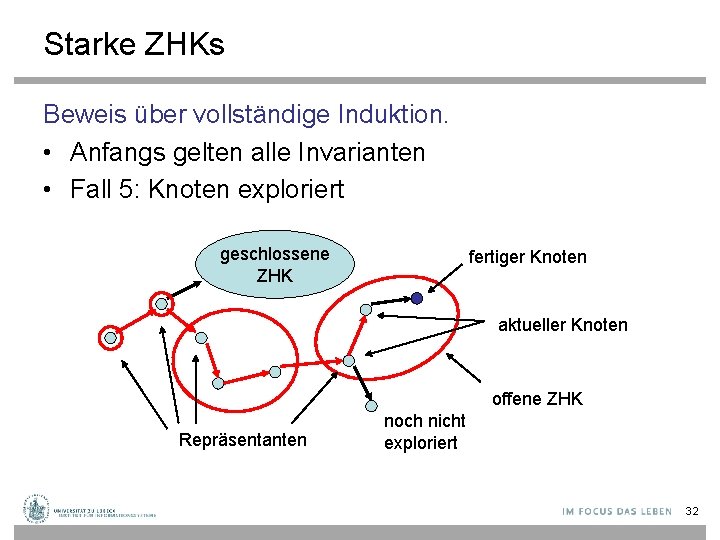
Starke ZHKs Beweis über vollständige Induktion. • Anfangs gelten alle Invarianten • Wir betrachten verschiedene Fälle geschlossene ZHK fertiger Knoten aktueller Knoten offene ZHK Repräsentanten noch nicht exploriert 27

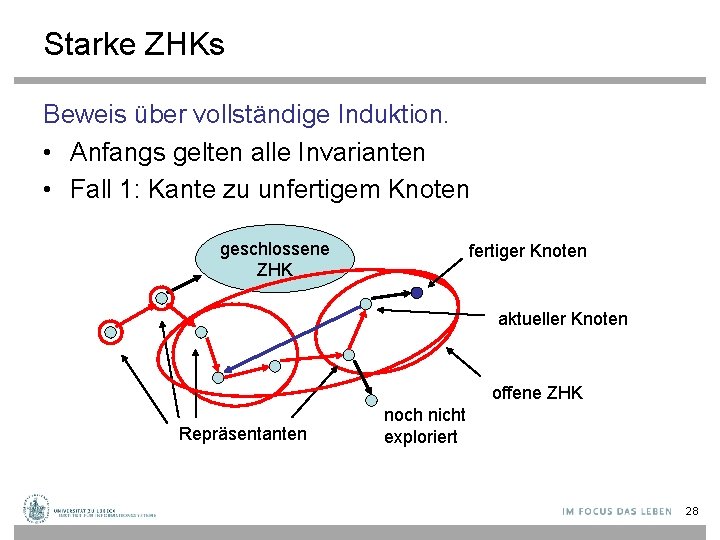
Starke ZHKs Beweis über vollständige Induktion. • Anfangs gelten alle Invarianten • Fall 1: Kante zu unfertigem Knoten geschlossene ZHK fertiger Knoten aktueller Knoten offene ZHK Repräsentanten noch nicht exploriert 28

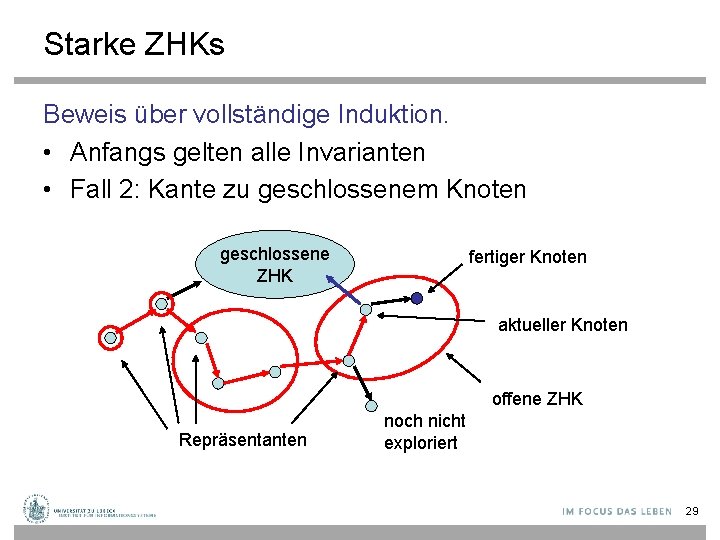
Starke ZHKs Beweis über vollständige Induktion. • Anfangs gelten alle Invarianten • Fall 2: Kante zu geschlossenem Knoten geschlossene ZHK fertiger Knoten aktueller Knoten offene ZHK Repräsentanten noch nicht exploriert 29

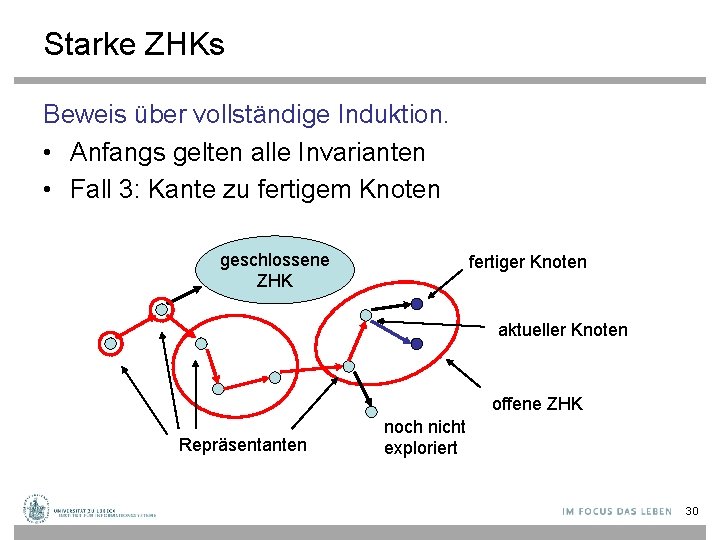
Starke ZHKs Beweis über vollständige Induktion. • Anfangs gelten alle Invarianten • Fall 3: Kante zu fertigem Knoten geschlossene ZHK fertiger Knoten aktueller Knoten offene ZHK Repräsentanten noch nicht exploriert 30

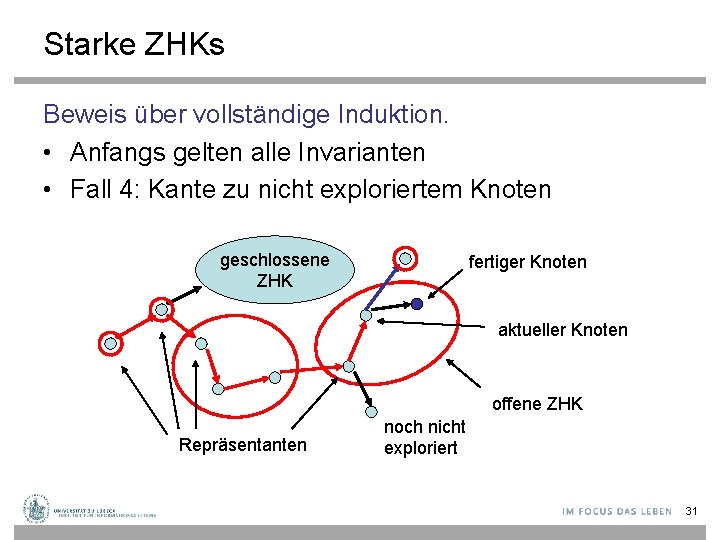
Starke ZHKs Beweis über vollständige Induktion. • Anfangs gelten alle Invarianten • Fall 4: Kante zu nicht exploriertem Knoten geschlossene ZHK fertiger Knoten aktueller Knoten offene ZHK Repräsentanten noch nicht exploriert 31

Starke ZHKs Beweis über vollständige Induktion. • Anfangs gelten alle Invarianten • Fall 5: Knoten exploriert geschlossene ZHK fertiger Knoten aktueller Knoten offene ZHK Repräsentanten noch nicht exploriert 32

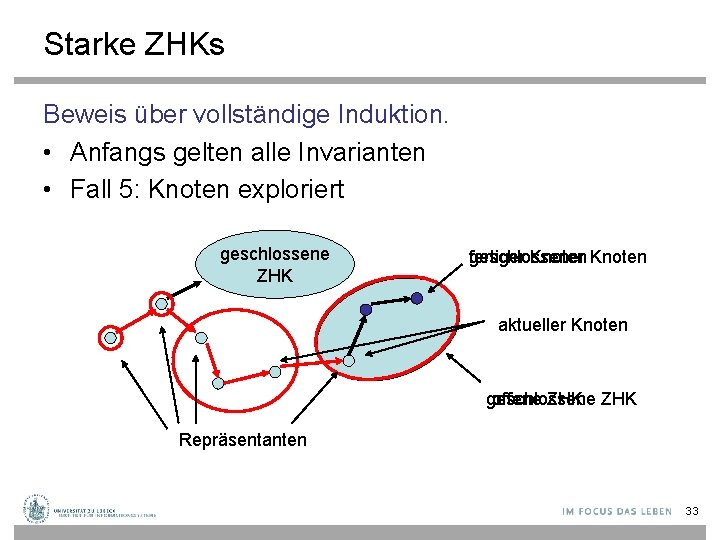
Starke ZHKs Beweis über vollständige Induktion. • Anfangs gelten alle Invarianten • Fall 5: Knoten exploriert geschlossene ZHK geschlossener fertiger Knoten aktueller Knoten geschlossene offene ZHK Repräsentanten 33

Starke ZHKs Behauptung: Eine geschlossene ZHK Gc im besuchten Teilgraphen C von G ist eine ZHK in G (die geschlossene ZHK Gc ist maximal) Überlegung: • v: geschlossener Knoten • S: ZHK in G, die v enthält • Sc: ZHK in Gc, die v enthält • Es gilt: Sc ⊆ S (v erreicht jeden Knoten in der ZHK) • Zu zeigen (Maximalität): S ⊆ Sc 34

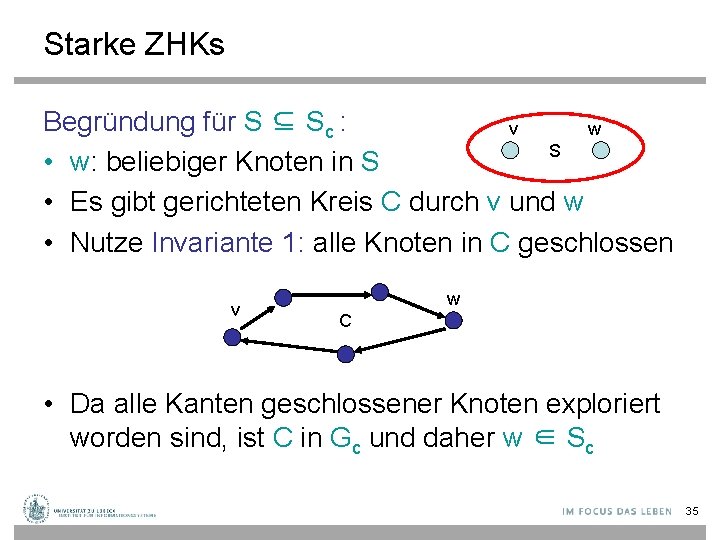
Starke ZHKs Begründung für S ⊆ Sc : v w S • w: beliebiger Knoten in S • Es gibt gerichteten Kreis C durch v und w • Nutze Invariante 1: alle Knoten in C geschlossen v w C • Da alle Kanten geschlossener Knoten exploriert worden sind, ist C in Gc und daher w ∈ Sc 35

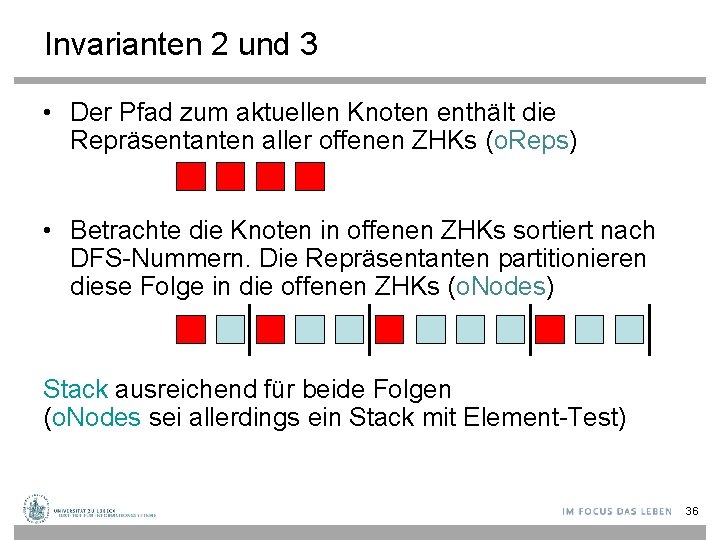
Invarianten 2 und 3 • Der Pfad zum aktuellen Knoten enthält die Repräsentanten aller offenen ZHKs (o. Reps) • Betrachte die Knoten in offenen ZHKs sortiert nach DFS-Nummern. Die Repräsentanten partitionieren diese Folge in die offenen ZHKs (o. Nodes) Stack ausreichend für beide Folgen (o. Nodes sei allerdings ein Stack mit Element-Test) 36

Wiederholung: Tiefensuche-Schema Übergeordnete Prozedur = Bestimme ZHKs unmark all nodes init() for s∈V do // stelle sicher, dass alle Knoten besucht werden if s is not marked then mark s root(s) DFS(s, s) // s: Startknoten Procedure DFS(u, v: Node) // u: Vater von v for (v, w)∈E do if w is marked then handle. Non. Tree. Edge(v, w) else traverse. Tree. Edge(v, w) mark w DFS(v, w) backtrack(u, v) Prozeduren in rot: noch zu spezifizieren 37
![Starke ZHKs init component Array 1 n of Node Id o Reps Starke ZHKs init(): component: Array [1. . n] of Node. Id o. Reps =](https://slidetodoc.com/presentation_image/4c16c3f15c6a1724eb17812e83cf8562/image-38.jpg)
Starke ZHKs init(): component: Array [1. . n] of Node. Id o. Reps = <>: Stack of Node. Id o. Nodes = <>: Stack of Node. Id dfs. Pos: =1 root(w) oder traverse. Tree. Edge(v, w): push(w, o. Reps) // neue ZHK push(w, o. Nodes) // neuer offener Knoten dfs. Num[w]: =dfs. Pos; dfs. Pos: =dfs. Pos+1 38

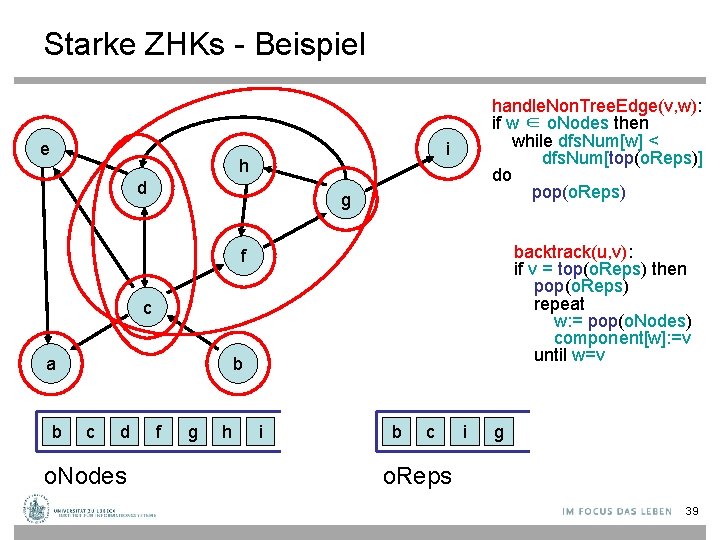
Starke ZHKs - Beispiel e handle. Non. Tree. Edge(v, w): if w ∈ o. Nodes then while dfs. Num[w] < dfs. Num[top(o. Reps)] do pop(o. Reps) i h d g backtrack(u, v): if v = top(o. Reps) then pop(o. Reps) repeat w: = pop(o. Nodes) component[w]: =v until w=v f c a b b c d a o. Nodes ef g h i b c a efi d h g o. Reps 39

Starke ZHKs Behauptung: Der DFS-basierte Algorithmus für starke ZHKs benötigt O(n+m) Zeit. Beweis: • init, root, traverse. Tree. Edge: Zeit O(1) • backtrack, handle. Non. Tree. Edge: da jeder Knoten nur höchstens einmal in o. Reps und o. Nodes landet, insgesamt Zeit O(n) Wie realisieren wir • DFS-Gerüst: Zeit O(n+m) einen Stack mit Element-Test, der in O(1) läuft? 40

Zusammenfassung • Traversierung: Tiefensuche Design Pattern • Gerichtete azyklische Graphen (DAGs) • Starke Zusammenhangskomponenten (ZHKs) • Im nächsten Teil: – Kürzeste Wege: Single-Source Shortest Paths 41