Algorithm Qualifying Examination Orals Achieving 100 Throughput in

Outline v v Introduction Part-I: Properties of Maximum Size Matching (MSM) in an IQ

Simple Model of a Switch R R Port 1, input Port 1, output Port

Input Queued Switch Model VOQs R Port 1, input Crossbar 1 1 Port N,

Relation to a Graph Matching VOQs 1 1 1 42 1 0 2 0

Classes of Scheduling Algorithms v Maximum Weight Matching (MWM) Ø Ø v Choose a

MSM is Unstable 1 1 Switch schedule based on MSM T=1 N N 1

Questions v Are all MSMs unstable? Ø Ø v Is there a subclass of

Non Pre-emptive Scheduling Batch-(k+1) R Batch-(k) Crossbar 1 Port 1, input 1 Port 1,

Degree of a Batch Degree (dv, k): Ø The number of cells departing from

Critical Maximum Size Matching Batch Request Graph 0 1 1 1 0 0 degree

The Arrival Process Algorithm Orals 2002 15

Stability of CMSM v Theorem 1: Ø v CMSM is stable under batch scheduling,

Formal Arguments … 1 v v We shall use the Chernoff bound to get

Formal Arguments … 2 v We can choose (1 + ) < 1 -

Formal Arguments … 3 v v Hence, there is a constant Tc which depends

Stability of CMSM v Theorem 2: CMSM is stable under batch scheduling, if the

Example of a Uniform Graph Batch Request Graph 1 1 1 degree =3 2

Properties of Uniform Graphs v Lemma-1: Ø v If the request graph is uniform

Property of any Graph v Theorem: Ø v Any request graph with maximum degree

Stability of MSM. . 1 v Theorem 3: MSM is stable under batch scheduling,

Maximal Matching Algorithms v Maximal Matching (MXM) Ø Ø Ø Choose a matching such

A Model for a CIOQ switch R R R Port 1 2 R 2

Leaky Bucket Traffic v v Let Aj(t 1, t 2) denote the number of

Stability of MXM v Theorem 4: A CIOQ switch with an MXM algorithm gives

Constraint Set ‘Maximal’ Algorithm v v v The algorithm is greedy i. e. when

Allocations as seen by the Output c k … DT + k DT v

Allocations as seen by the Input c B+k k … DT + k DT

Sufficiency Conditions on Speedup v We are guaranteed a timeslot if v The above

Stability of MXM v Theorem 5: A CIOQ switch with an MXM algorithm gives

Summary v In an IQ switch with batch scheduling Ø Ø v A subclass

Future Questions v We have seen that MSM is stable under the auspices of

Stability of MSM … 2 v Informal Arguments: Ø Similar to the CMSM proof,

Slides: 39

Download presentation

Algorithm Qualifying Examination Orals Achieving 100% Throughput in IQ/CIOQ Switches using Maximum Size and Maximal Matching Algorithms Sundar Iyer Stanford University sundaes@cs. stanford. edu www. stanford. edu/~sundaes August 21 st, 2001 1

Outline v v Introduction Part-I: Properties of Maximum Size Matching (MSM) in an IQ switch Ø Ø v Stability of critical MSM for any Bernoulli i. i. d. traffic Stability of MSM for Bernoulli i. i. d. uniform traffic Part-II: Properties of Maximal Matching (MXM) in a CIOQ switch Ø A simple proof for stability Algorithm Orals 2002 2

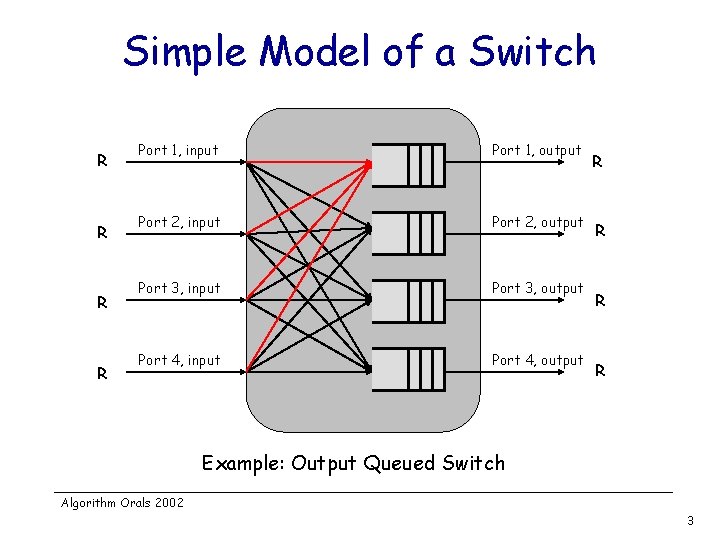
Simple Model of a Switch R R Port 1, input Port 1, output Port 2, input Port 2, output Port 3, input Port 3, output Port 4, input Port 4, output R R Example: Output Queued Switch Algorithm Orals 2002 3

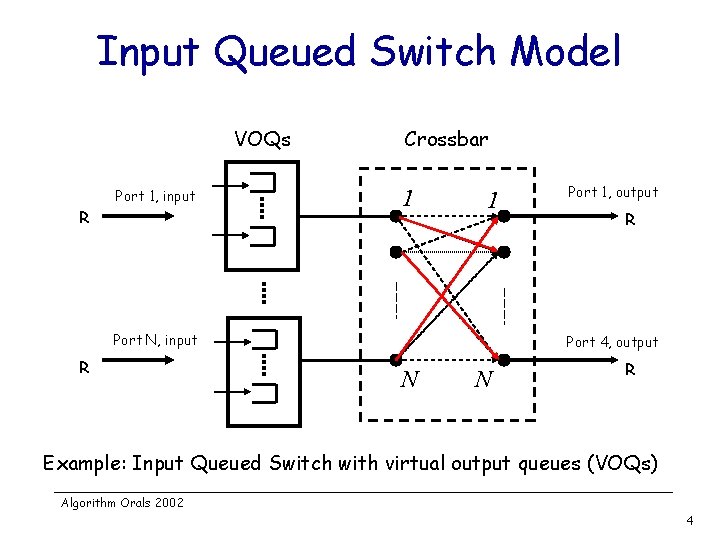
Input Queued Switch Model VOQs R Port 1, input Crossbar 1 1 Port N, input R Port 1, output R Port 4, output N N R Example: Input Queued Switch with virtual output queues (VOQs) Algorithm Orals 2002 4

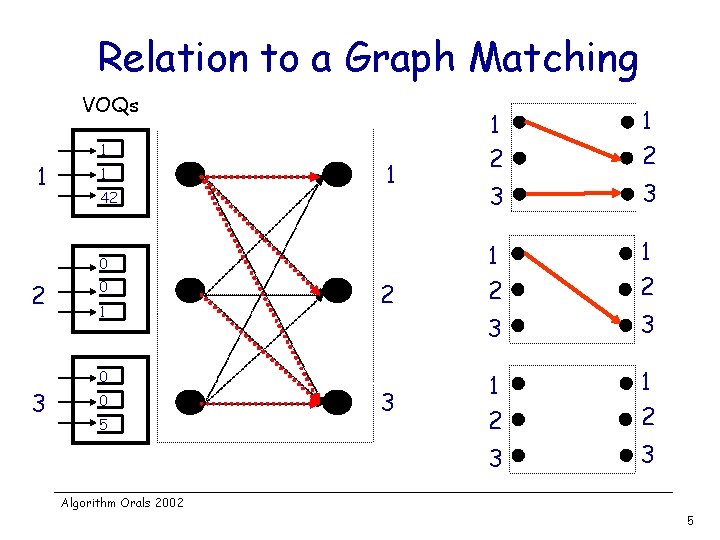
Relation to a Graph Matching VOQs 1 1 1 42 1 0 2 0 1 0 3 0 5 2 3 1 2 1 2 3 3 Algorithm Orals 2002 5

Classes of Scheduling Algorithms v Maximum Weight Matching (MWM) Ø Ø v Choose a matching which maximizes the weight of the matching MWM gives 100% throughput Maximum Size Matching (MSM) Ø Choose a matching which maximizes the size of the matching Algorithm Orals 2002 6

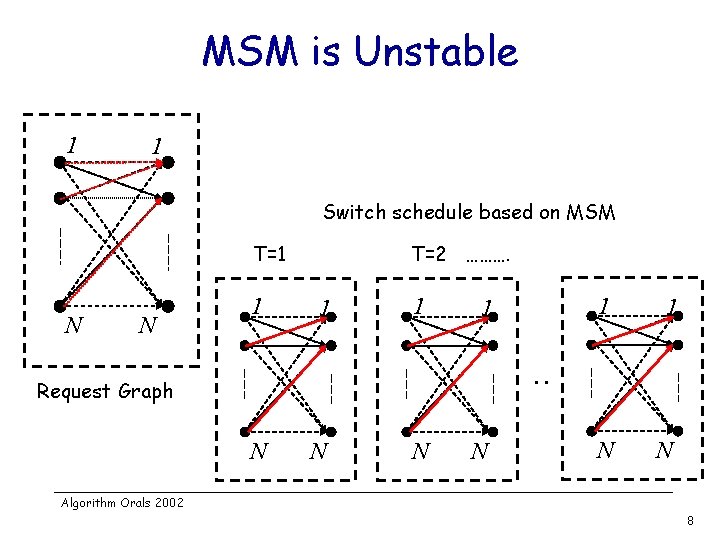
MSM is Unstable 1 1 Switch schedule based on MSM T=1 N N 1 T=2 ………. 1 1 1 N N . . Request Graph N N Algorithm Orals 2002 8

Questions v Are all MSMs unstable? Ø Ø v Is there a subclass of MSMs which are stable? There is at least one MSM which is stable. Are MSMs stable under uniform load? Ø Ø Simulation seems to suggest this. Can we prove this? Algorithm Orals 2002 9

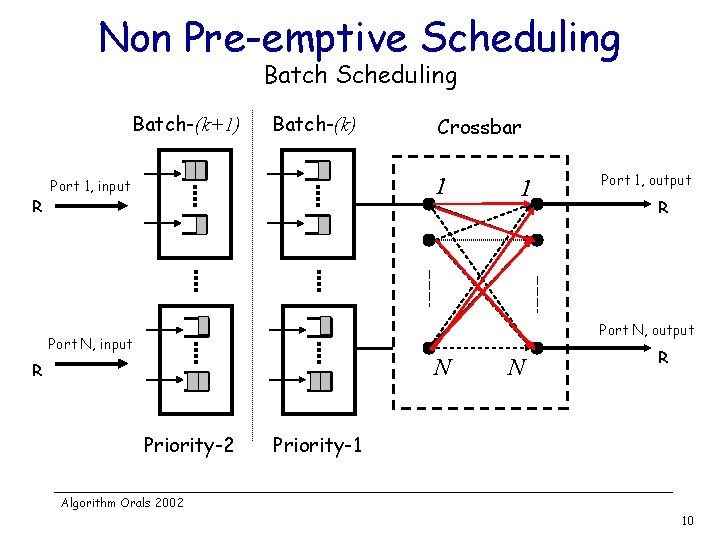
Non Pre-emptive Scheduling Batch-(k+1) R Batch-(k) Crossbar 1 Port 1, input 1 Port 1, output R Port N, output Port N, input N R Priority-2 N R Priority-1 Algorithm Orals 2002 10

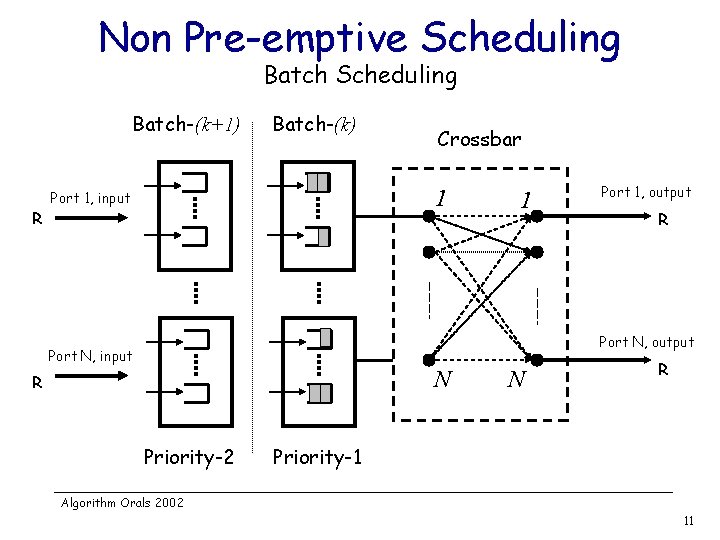
Non Pre-emptive Scheduling Batch-(k+1) R Batch-(k) Crossbar 1 Port 1, input 1 Port 1, output R Port N, output Port N, input N R Priority-2 N R Priority-1 Algorithm Orals 2002 11

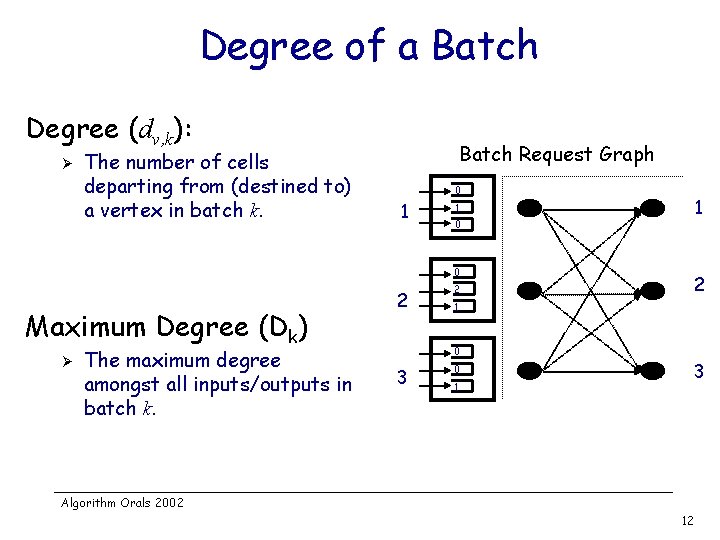
Degree of a Batch Degree (dv, k): Ø The number of cells departing from (destined to) a vertex in batch k. Batch Request Graph 0 1 0 0 Maximum Degree (Dk) Ø The maximum degree amongst all inputs/outputs in batch k. 2 2 2 1 0 3 1 1 0 1 3 Algorithm Orals 2002 12

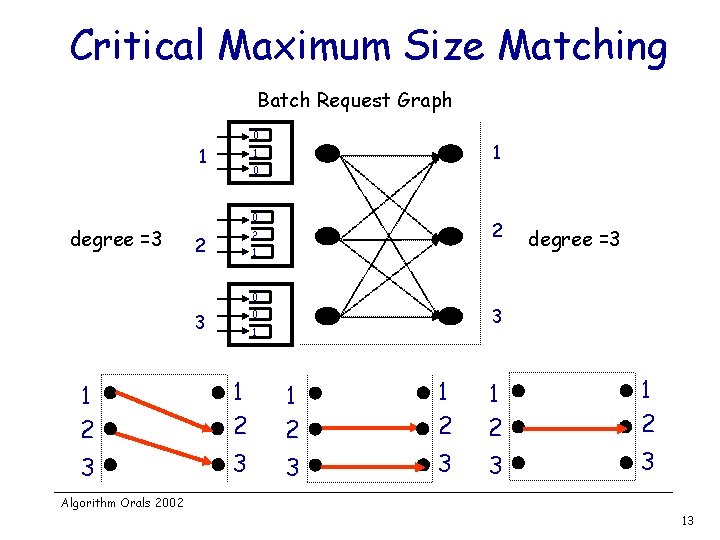
Critical Maximum Size Matching Batch Request Graph 0 1 1 1 0 0 degree =3 2 2 2 1 0 3 degree =3 1 1 2 1 2 1 2 3 3 3 Algorithm Orals 2002 13

Outline v v Introduction Part-I: Properties of Maximum Size Matching (MSM) in an IQ switch Ø Ø v Stability of Critical MSM for any Bernoulli i. i. d. traffic Stability of MSM for Bernoulli i. i. d. uniform traffic Part-II: Properties of Maximal Matching (MXM) in a CIOQ switch Ø A Simple proof for stability Algorithm Orals 2002 14

The Arrival Process Algorithm Orals 2002 15

Stability of CMSM v Theorem 1: Ø v CMSM is stable under batch scheduling, if the input traffic is admissible and Bernoulli i. i. d. uniform Informal Arguments: Ø Ø Ø Let Tk be the time to schedule batch k Then for batch k+1 we buffer packets for time Tk We expect about Tk packets at every input/output Hence, the maximum degree of batch k +1, i. e. Dk+1 Tk Hence for a CMSM Tk+1 = Dk+1 = Tk < Tk Hence Tk converges to a finite number Algorithm Orals 2002 16

Formal Arguments … 1 v v We shall use the Chernoff bound to get If we want to bound Dk, we require that all the 2 N vertices are bounded Algorithm Orals 2002 17

Formal Arguments … 2 v We can choose (1 + ) < 1 - to get v Observe that Ø Ø Ø v Q is now a function of Tk only. We can make Q as close to 1, by choosing a large Tk Also, Tk+1 NTk This gives Algorithm Orals 2002 18

Formal Arguments … 3 v v Hence, there is a constant Tc which depends only on (and hence only on ), such that Formally, using a linear Lyapunov function V(Tk) = Tk, we can say that E(Tk) is bounded. Algorithm Orals 2002 19

Stability of CMSM v Theorem 2: CMSM is stable under batch scheduling, if the input traffic is admissible and Bernoulli i. i. d. Algorithm Orals 2002 20

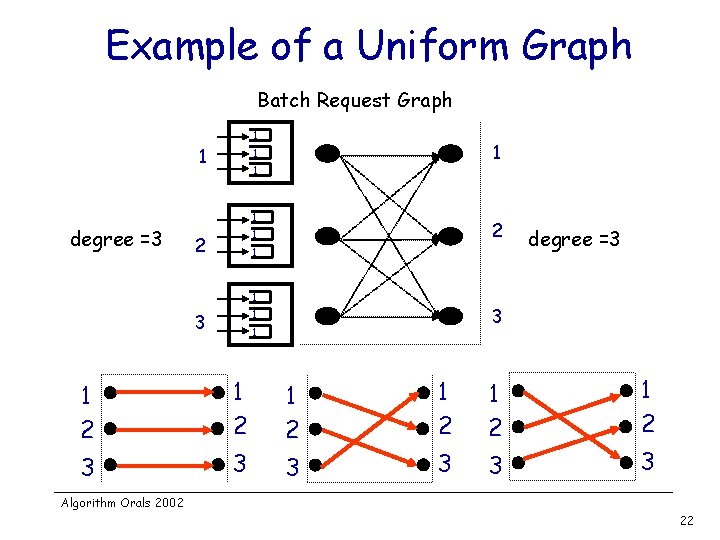
Example of a Uniform Graph Batch Request Graph 1 1 1 degree =3 2 1 1 3 degree =3 1 1 2 1 2 1 2 3 3 3 Algorithm Orals 2002 22

Properties of Uniform Graphs v Lemma-1: Ø v If the request graph is uniform and the maximum degree is D, then any MSM can schedule the requests in exactly D time slots Lemma-2: Ø Any request graph with maximum degree D, can be scheduled by any MSM within 2 D time slots Algorithm Orals 2002 23

Property of any Graph v Theorem: Ø v Any request graph with maximum degree is D, and minimum VOQ length m, can be scheduled in less than 2 D –Nm time slots Proof: Ø Ø Ø Consider a request graph with minimum VOQ length m The minimum degree of the graph is m. N Hence the original graph can be considered to be in two parts • A uniform graph of degree m. N • Another graph of maximum degree D – m. N Ø Hence the request graph can be scheduled in at most m. N + 2(D-m. N) = 2 D - Nm Algorithm Orals 2002 24

Stability of MSM. . 1 v Theorem 3: MSM is stable under batch scheduling, if the input traffic is admissible and Bernoulli i. i. d. uniform v Informal Arguments Ø Ø We can bound both the maximum degree D and the minimum VOQ length m The rest of the proof is similar to the CMSM proof Algorithm Orals 2002 25

Maximal Matching Algorithms v Maximal Matching (MXM) Ø Ø Ø Choose a matching such that no unmatched input or output has a packet meant for each other They are easier to implement and have low complexity They are known to be unstable and give low throughput for input queued switches Algorithm Orals 2002 27

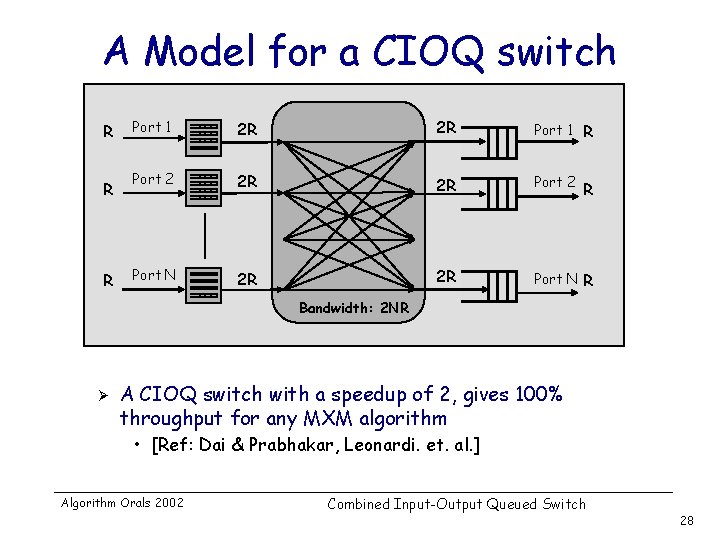
A Model for a CIOQ switch R R R Port 1 2 R 2 R Port 1 R Port 2 2 R 2 R Port 2 Port N 2 R 2 R Port N R R Bandwidth: 2 NR Ø A CIOQ switch with a speedup of 2, gives 100% throughput for any MXM algorithm • [Ref: Dai & Prabhakar, Leonardi. et. al. ] Algorithm Orals 2002 Combined Input-Output Queued Switch 28

Leaky Bucket Traffic v v Let Aj(t 1, t 2) denote the number of arrivals to output j in the interval between (t 1, t 2) A leaky bucket constrained traffic satisfies, the property that for each output j Note that this means that for an ideal output queued switch no output has more than B packets in the switch Let DT denote the departure time of a packet from this ‘ideal’ output queued switch Algorithm Orals 2002 29

Stability of MXM v Theorem 4: A CIOQ switch with an MXM algorithm gives bounded delay and hence 100% throughput with a speedup greater than 2, under arrivals which satisfy the leaky bucket constraint Algorithm Orals 2002 30

Constraint Set ‘Maximal’ Algorithm v v v The algorithm is greedy i. e. when a cell arrives, it immediately attempts to allot a time (in the future) when it should be transferred Each input and output maintains a constraint set of the future times during which it is free to send/receive a packet The algorithm attempts to bound the time of departure of a packet to within k time slots of its departure time DT, i. e each packet is transferred in the time (DT, DT+k) Algorithm Orals 2002 31

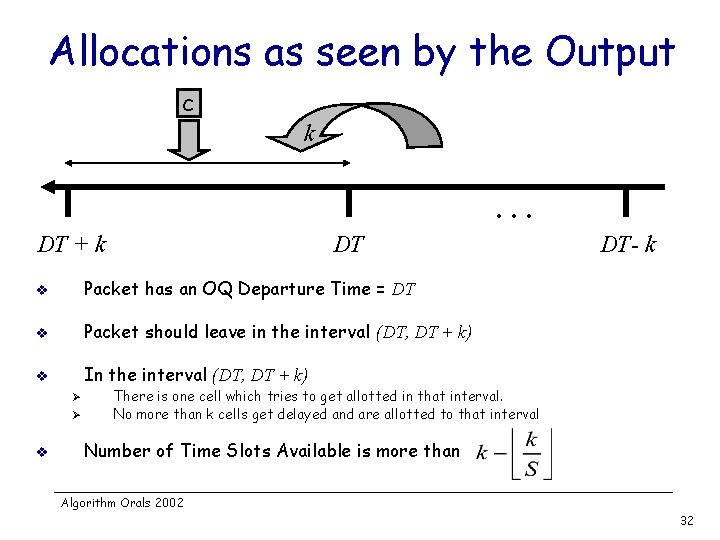
Allocations as seen by the Output c k … DT + k DT v Packet has an OQ Departure Time = DT v Packet should leave in the interval (DT, DT + k) v In the interval (DT, DT + k) Ø Ø v DT- k There is one cell which tries to get allotted in that interval. No more than k cells get delayed and are allotted to that interval Number of Time Slots Available is more than Algorithm Orals 2002 32

Allocations as seen by the Input c B+k k … DT + k DT v Packet has an OQ Departure Time = DT v Packet should leave during interval (DT, DT + k) v In the interval (DT, DT + k) Ø Ø v DT-B-k There is one cell which tries to get allotted in that interval No cell which arrived before DT–B-k will be allotted to this interval Number of Time Slots Available is more than Algorithm Orals 2002 33

Sufficiency Conditions on Speedup v We are guaranteed a timeslot if v The above equation can be satisfied if v v This means S > 2 is sufficient to guarantee that the delay is bounded This implies 100% throughput Algorithm Orals 2002 34

Stability of MXM v Theorem 5: A CIOQ switch with an MXM algorithm gives 100% throughput with a speedup greater than 2, under admissible arrivals which satisfy the strong law of large numbers Algorithm Orals 2002 35

Summary v In an IQ switch with batch scheduling Ø Ø v A subclass of MSM called CMSM is stable, if the input traffic is admissible and Bernoulli i. i. d. uniform In a CIOQ switch with S>2, Ø MXM is stable under any traffic which satisfies the strong law of large numbers Algorithm Orals 2002 36

Future Questions v We have seen that MSM is stable under the auspices of batch scheduling Ø v v Perhaps we could incorporate this (well known) idea into a number of other algorithms to prove stability? It would be nice to nail down the stability of MSM with uniform load in the absence of batch scheduling Other open questions remain Algorithm Orals 2002 37

Backup Algorithm Orals 2002 38

Stability of MSM … 2 v Informal Arguments: Ø Similar to the CMSM proof, derive P{D < (1 + 1) Tk } Ø Use Chernoff bound, to derive P{m. N > (1 - 2) Tk} Ø We can now write the probability of using less than 2[(1 + 1) Tk] – (1 - 2) Tk = (1 + 2) Tk time slots Ø Then rest of the proof is similar to CMSM Algorithm Orals 2002 39