Algorithm for Fast MC Simulation of Proteins Itay

Algorithm for Fast MC Simulation of Proteins Itay Lotan Fabian Schwarzer Dan Halperin Jean-Claude Latombe

MC Simulation • Classic technique for studying thermodynamic properties of proteins • Random walk through conformation space: – Propose random change in conformation – Accept new conformation with probability that depends on difference in energy (Metropolis criterion):

Our Contribution A generic algorithm for MCS which has: – Efficient incremental update of conformation given m simultaneous changes – Efficient computation of energy terms – Reuse of unchanged energy terms The algorithm supports most molecule representations, energy functions and simulation methodologies

Requirements 1. Small number of DOF changes per step 2. Energy function with: A. Bonded terms (bond length, bond angle, etc. ) B. Pairwise non-bonded terms (vd. W, elctrostatic, etc. ) with cutoff distances

Useful Properties of MCS • A protein is a long kinematic chain • Small number of changes large rigid sub-chains • Cutoff distance small subset of all pairs is needed • Many energy terms can be reused

Challenges • How to update the conformation without re-computing the position of all atoms? • How to efficiently find all pairs of atoms whose distance is below the cutoff (interacting pairs)? • How to efficiently discover which energy terms have changed and which can be reused?

Related Work The algorithm is based on a self-collision detection method for kinematic chains we presented at So. CG 02 Biologists have used many tricks and heuristics to speed up their simulations. There is no general method exploiting common properties of all MCS exists

Molecule Representation Twofold hierarchical structure: • Transformations hierarchy to approximate the kinematics of the protein at different resolutions • Bounding Volume hierarchy to approximate the geometry of the protein at different resolutions

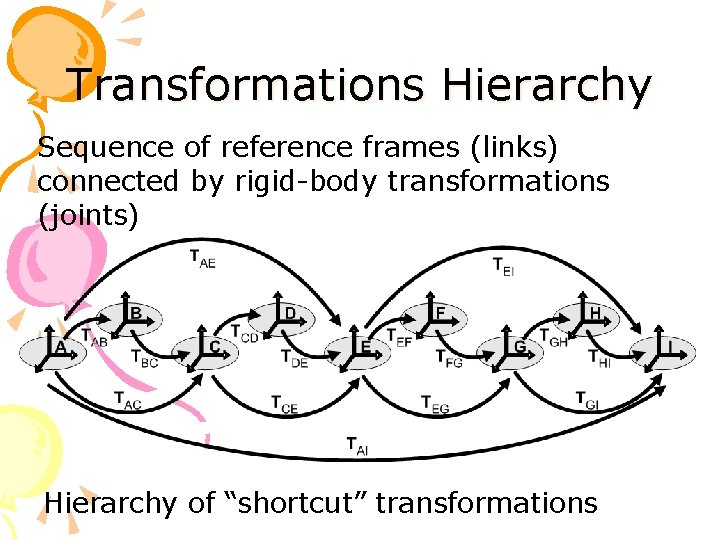
Transformations Hierarchy Sequence of reference frames (links) connected by rigid-body transformations (joints) Hierarchy of “shortcut” transformations

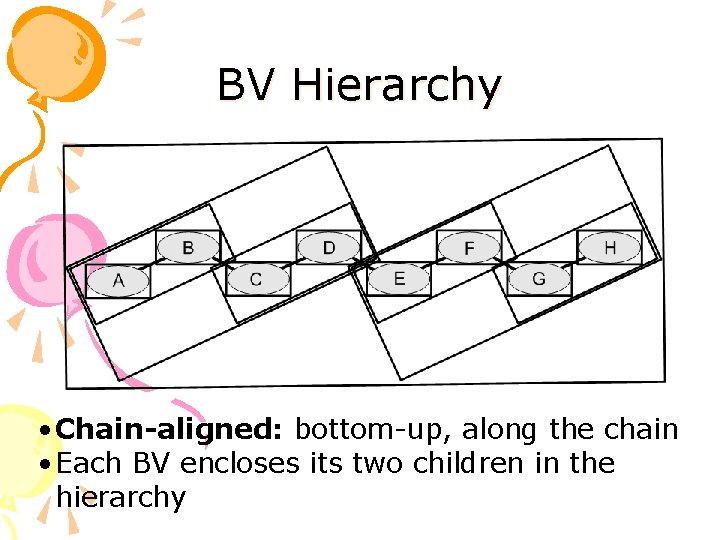
BV Hierarchy • Chain-aligned: bottom-up, along the chain • Each BV encloses its two children in the hierarchy

Computing distances - RSS • RSS (rectangle swept sphere) - The Minkowski sum of a rectangle and a sphere (Larsen et al. , ICRA 2000)

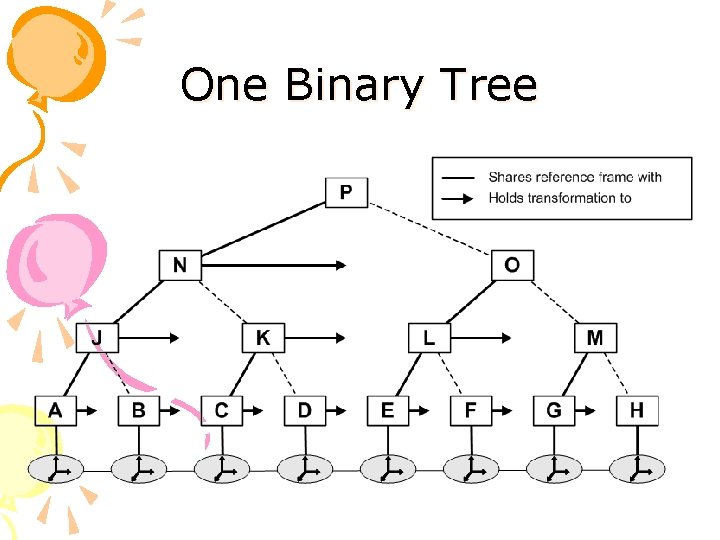
One Binary Tree

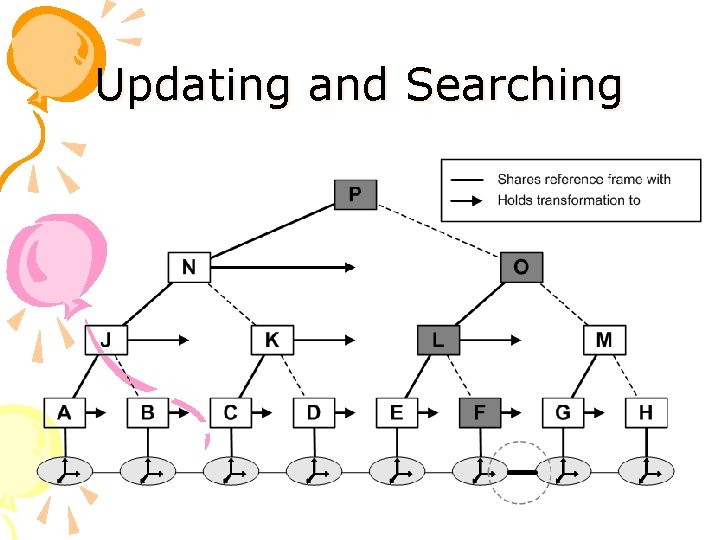
Updating and Searching

Complexity • Updating: • Finding all interacting pairs: Worst-case Performs much better in practice!!!

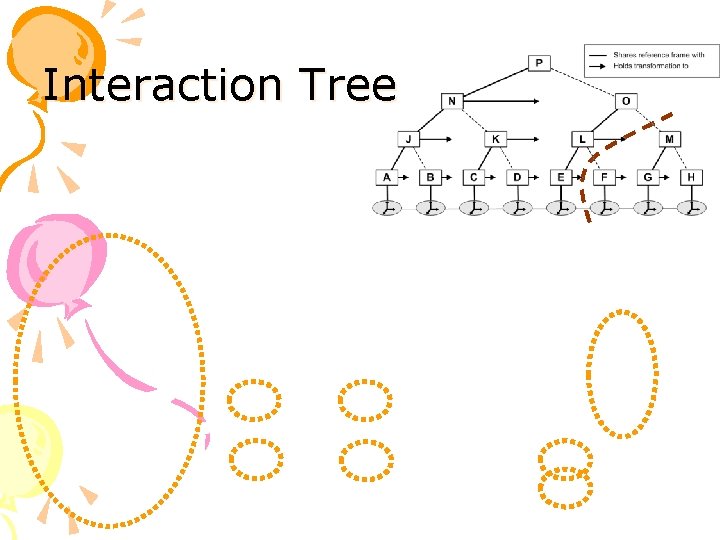
Interaction Tree • Hierarchy of possible interactions between sub-chains of the protein • Based on our hierarchical representation of the protein • Stores partial sums of non-bonded pairwise energy terms • Allows efficient reuse of unchanged terms

Interaction Tree

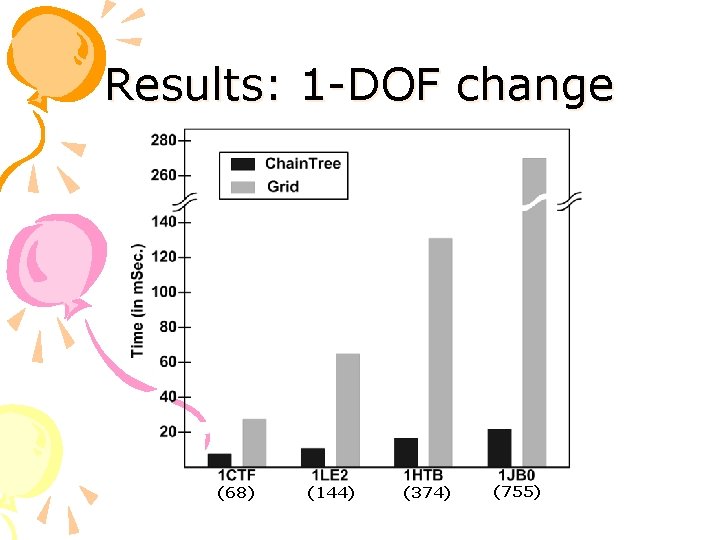
Results: 1 -DOF change (68) (144) (374) (755)

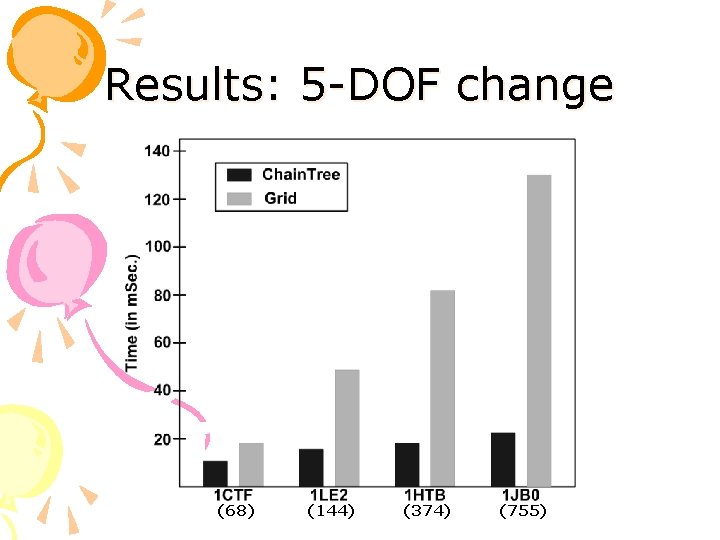
Results: 5 -DOF change (68) (144) (374) (755)

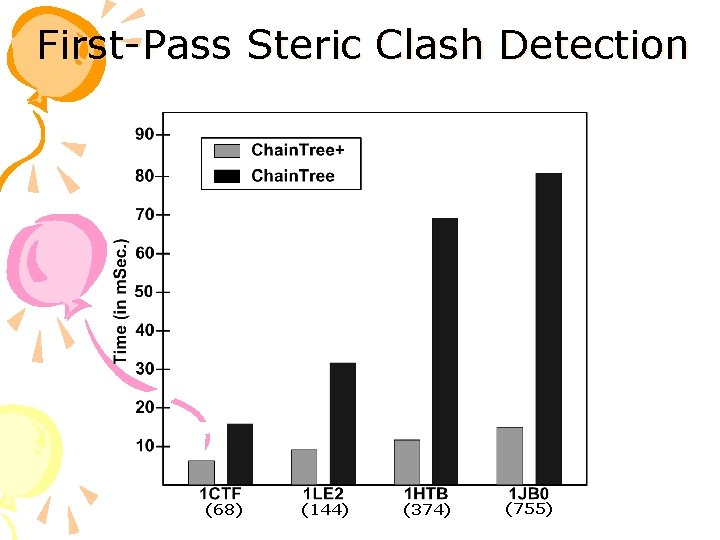
First-Pass Steric Clash Detection (68) (144) (374) (755)

What next? • Implement a real force field: EEF 1 (Lazaridis & Karplus) • Based on CHARMM 19 • 9Å cutoff distance • Implicit solvent as sum of pairwise terms • Run MCS of proteins with 60 – 80 residues. • Run simulation of a set of small proteins – misfolding.

Open Problem • How to find good moves to make when the conformation becomes compact and random moves are rejected with high probability?