Algorithm Efficiency There are often many approaches algorithms

Algorithm Efficiency There are often many approaches (algorithms) to solve a problem. How do we choose between them? At the heart of computer program design are two (sometimes conflicting) goals. 1. To design an algorithm that is easy to understand, code, debug. 2. To design an algorithm that makes efficient use of the computer’s resources. 7

Algorithm Efficiency (cont) Goal (1) is the concern of Software Engineering. Goal (2) is the concern of data structures and algorithm analysis. When goal (2) is important, how do we measure an algorithm’s cost? 8

How to Measure Efficiency? 1. Empirical comparison (run programs) 2. Asymptotic Algorithm Analysis Critical resources: Factors affecting running time: For most algorithms, running time depends on “size” of the input. Running time is expressed as T(n) for some function T on input size n. 9

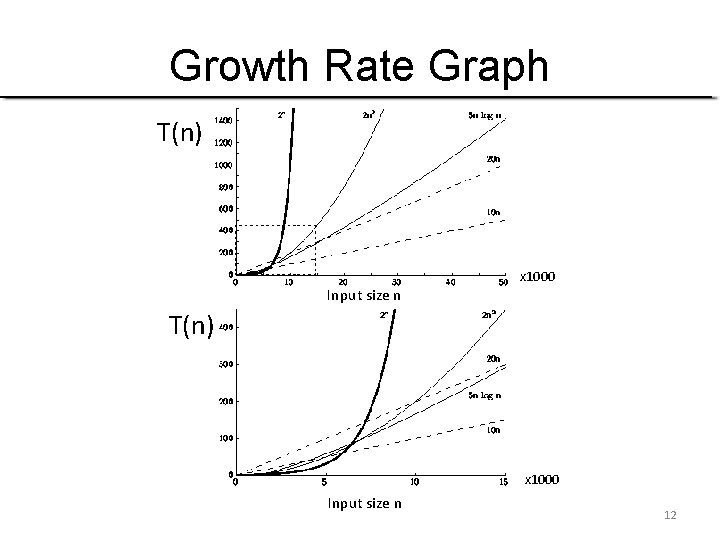
Growth Rate The growth rate for an algorithm is the rate at which the cost (running time) of the algorithm grows as the size of its input grows. 11

Growth Rate Graph T(n) Input size n x 1000 T(n) x 1000 Input size n 12

Examples of Growth Rate (1) for (i=1; i<=1000; i=i+1) <<application code>>; 1000 times for (i=1; i<=1000; i=i+2) 500 times <<application code>>; for (i=1; i<1000; i=i*2) <<application code>>; 10 times for (i=1000; i>=1; i=i/2) 10 times <<application code>>; 15

Examples (2) for (j=1; j<=10; j=j+1) 10 times for (i=1; i<=10; i=i+1) 10 iterations <<application code>>; 100 iterations for (j=1; j<=10; j=j+1) 10 iterations for (i=1; i<=10; i=i*2) log 210 iterations <<application code>>; 10*log 210 iterations for (j=1; j<=10; j=j+1) 10 times for (i=1; i<=j; i=i+1) (10+1)/2 times <<application code>>; 55 iterations 16

Example: Input Size = n for (i=1; i<=n; i=i+1) <<application code>>; T(n) = n for (i=1; i<=n; i=i+2) <<application code>>; T(n) = n/2 for (i=1; i<n; i=i*2) <<application code>>; T(n) for (i=n; i>=1; i=i/2) <<application code>>; 17

Examples (2) for (j=1; j<=n; j=j+1) for (i=1; i<=n; i=i+1) <<application code>>; for (j=1; j<=n; j=j+1) for (i=1; i<=n; i=i*2) <<application code>>; for (j=1; j<=n; j=j+1) for (i=1; i<=j; i=i+1) <<application code>>; 18

Examples (3) // Find largest value int largest(int array[], int n) { int currlarge = 0; // Largest value seen for (int i=1; i<n; i++) // For each val if (array[currlarge] < array[i]) currlarge = i; // Remember pos return currlarge; // Return largest } 19

Time Complexity • Best Case Time Complexity – เวลาทดสด (minimum time) ��� algorithm ������������� n • Worst Case Time Complexity – เวลาทมากสด (maximum time) ��� algorithm ������������� n – ���������� algorithm ������������� – ����� time-critical software application • Average Case Time Complexity – เวลาทเฉลย (average time) ��� algorithm ������������� n – Need assumption about inputs’ distribution

Best, Worst, Average Cases Sequential search for K in an array of n integers: • Begin at first element in array and look at each element in turn until K is found Best case: Worst case: Average case: 21

Which Analysis to Use? While average time appears to be the fairest measure, it may be difficult to determine. When is the worst case time important? 22

Big-O Notation Big-oh notation represents the growth rate. It's useful to be able to estimate the cpu or memory resources an algorithm requires. Example: If T(n) = 3 n 2 then T(n) is in O(n 2). Wish tightest upper bound: While T(n) = 3 n 2 is in O(n 3), we prefer O(n 2). 23

Big-Oh Examples Example 1: Finding value X in an array T(n) is in O(n). Example 2: T(n) = c 1 n 2 + c 2 n T(n) is in O(n 2). Example 3: T(n) = c. We say this is in O(1). 24

Running Time Examples (1) Example 1: O(1) a = b; This assignment takes constant time, so it is O(1). Example 2: O(n) sum = 0; for (i=1; i<=n; i++) sum += n; O(n) 25

Running Time Examples (2) Example 3: O(n 2) sum = 0; O(1) for (j=1; j<=n; j++) for (i=1; i<=j; i++) sum++; O(n 2) for (k=0; k<n; k++) A[k] = k; O(n) 26

Running Time Examples (3) Example 4: O(n 2) sum 1 = 0; O(1) for (i=1; i<=n; i++) for (j=1; j<=n; j++) sum 1++; O(n 2) sum 2 = 0; O(1) for (i=1; i<=n; i++) for (j=1; j<=i; j++) sum 2++; O(n 2) sum is n 2. sum is (n+1)(n)/2. 27

Running Time Examples (4) Example 5: O(nlogn) sum 1 = 0; for (k=1; k<=n; k*=2) for (j=1; j<=n; j++) sum 1++; O(logn) O(n) sum 2 = 0; for (k=1; k<=n; k*=2) for (j=1; j<=k; j++) sum 2++; O(n) First loop is n for k = 1 to log n. Second loop is 2 k for k = 0 to log n.

Algorithm Efficiency Constant iในแถวลำดบ O(1) การขาถงสมาชกตวท Logarithmic O(logn) การคนหาแบบ Binary Search Linear O(n) การคนหาแบบ Sequential Search Linear logarithmic O(n(logn)) การจดเรยงแบบ Quadratic การจดเรยงแบบธรรมดา O(n 2) Merge Sort 29

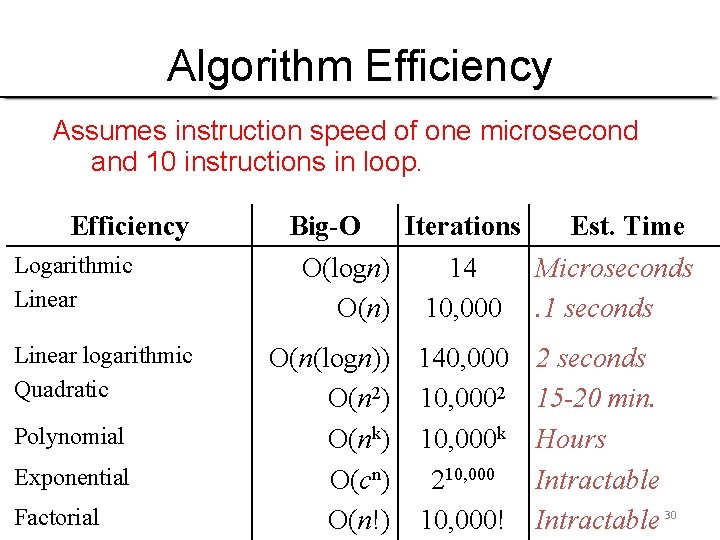
Algorithm Efficiency Assumes instruction speed of one microsecond and 10 instructions in loop. Efficiency Logarithmic Linear logarithmic Quadratic Polynomial Exponential Factorial Big-O Iterations Est. Time O(logn) 14 Microseconds O(n) 10, 000. 1 seconds O(n(logn)) 140, 000 2 seconds O(n 2) 10, 0002 15 -20 min. O(nk) 10, 000 k Hours O(cn) 210, 000 Intractable O(n!) 10, 000! Intractable 30

Faster Computer or Algorithm? Old machine can run 10, 000 basic operations/hour. What happens when we buy a computer 10 New machine can run 100, 000 basic operations/hour. times faster? T(n) n n’ Change n’/n Algorithm����� growth rate 10 n 1, 000 10, 000 n’ = 10 n 10 ������������������������� 20 n 500 5, 000 n’ = 10 n 10 ������������� 5 n log n 250 1, 842 10 n < n’ < 10 n 7. 37 � 2 n 2 70 223 n’ = 10 n 3. 16 2 n 13 16 n’ = n + 3 ----31