Algorithm Efficiency How do we measure efficiency Space

Algorithm Efficiency • How do we measure efficiency – Space utilization – amount of memory required – Time required to accomplish the task • Time efficiency depends on : – size of input – speed of machine – quality of source code – quality of compiler These vary from one platform to another Nyhoff, ADTs, Data Structures and Problem Solving with C++, Second Edition, © 2005 Pearson Education, Inc. All rights reserved. 0 -13 -140909 -3 1

Algorithm Efficiency • We can count the number of times instructions are executed – This gives us a measure of efficiency of an algorithm • So we measure computing time as: T(n)= computing time of an algorithm for input of size n = number of times the instructions are executed Nyhoff, ADTs, Data Structures and Problem Solving with C++, Second Edition, © 2005 Pearson Education, Inc. All rights reserved. 0 -13 -140909 -3 2

Example: Calculating the Mean Task 1. 2. 3. 4. 5. 6. # times executed Initialize the sum to 0 Initialize index i to 0 While i < n do following a) Add x[i] to sum b) Increment i by 1 Return mean = sum/n Total 1 1 n+1 n n 1 3 n + 4 Nyhoff, ADTs, Data Structures and Problem Solving with C++, Second Edition, © 2005 Pearson Education, Inc. All rights reserved. 0 -13 -140909 -3 3

Computing Time Order of Magnitude • As number of inputs increases § T(n) = 3 n + 4 grows at a rate proportional to n • Thus T(n) has the "order of magnitude" n • The computing time of an algorithm on input of size n, § T(n) said to have order of magnitude f(n), § written T(n) is O(f(n)) iff … there is some constant C such that § T(n) < C f(n) for all sufficiently large values of n Nyhoff, ADTs, Data Structures and Problem Solving with C++, Second Edition, © 2005 Pearson Education, Inc. All rights reserved. 0 -13 -140909 -3 4

Big Oh Notation Another way of saying this: • The complexity of the algorithm is O(f(n)). • Example: For the Mean-Calculation Algorithm: T(n) is O(n) • Note that constants and multiplicative factors are ignored. Nyhoff, ADTs, Data Structures and Problem Solving with C++, Second Edition, © 2005 Pearson Education, Inc. All rights reserved. 0 -13 -140909 -3 5

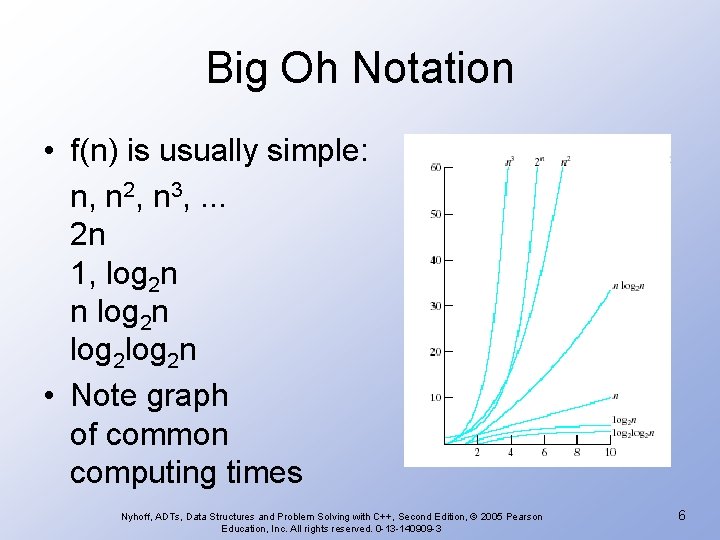
Big Oh Notation • f(n) is usually simple: n, n 2, n 3, . . . 2 n 1, log 2 n n log 2 log 2 n • Note graph of common computing times Nyhoff, ADTs, Data Structures and Problem Solving with C++, Second Edition, © 2005 Pearson Education, Inc. All rights reserved. 0 -13 -140909 -3 6

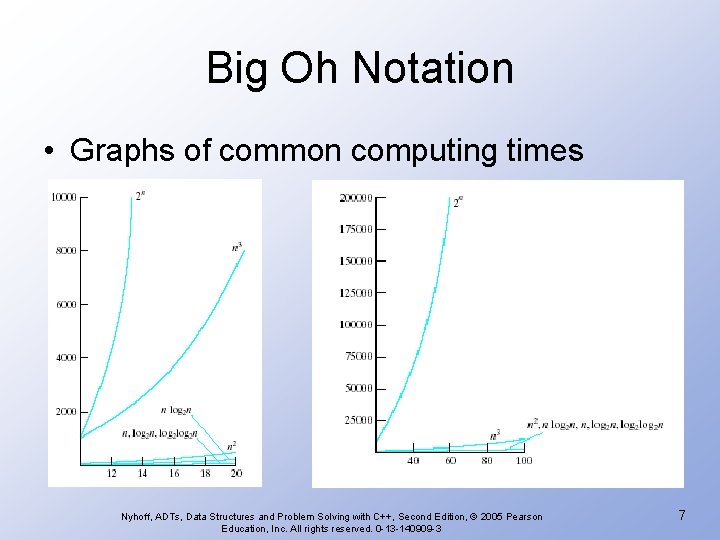
Big Oh Notation • Graphs of common computing times Nyhoff, ADTs, Data Structures and Problem Solving with C++, Second Edition, © 2005 Pearson Education, Inc. All rights reserved. 0 -13 -140909 -3 7

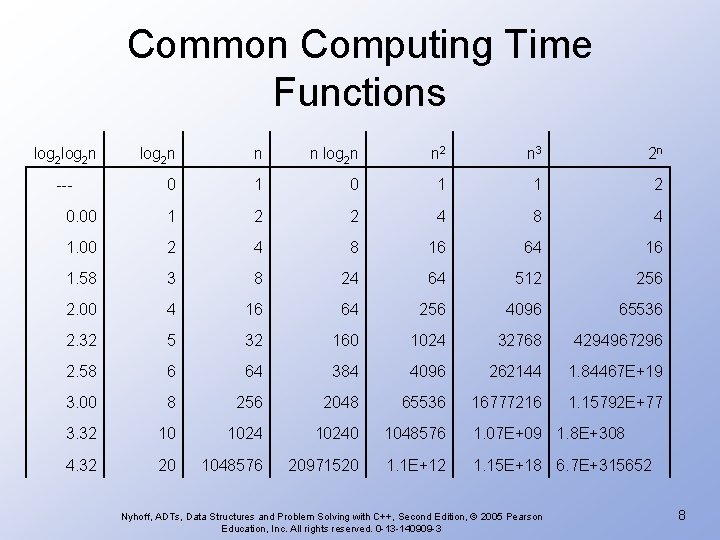
Common Computing Time Functions log 2 n n 2 n 3 2 n 0 1 1 2 0. 00 1 2 2 4 8 4 1. 00 2 4 8 16 64 16 1. 58 3 8 24 64 512 256 2. 00 4 16 64 256 4096 65536 2. 32 5 32 160 1024 32768 4294967296 2. 58 6 64 384 4096 262144 1. 84467 E+19 3. 00 8 256 2048 65536 16777216 1. 15792 E+77 3. 32 10 10240 1048576 1. 07 E+09 1. 8 E+308 4. 32 20 1048576 20971520 1. 1 E+12 1. 15 E+18 6. 7 E+315652 --- Nyhoff, ADTs, Data Structures and Problem Solving with C++, Second Edition, © 2005 Pearson Education, Inc. All rights reserved. 0 -13 -140909 -3 8

Computing in Real Time • Suppose each instruction can be done in 1 microsecond • For n = 256 inputs how long for various f(n) Function Time log 2 n 3 microseconds Log 2 n 8 microseconds n . 25 milliseconds n log 2 n 2 milliseconds n 2 65 milliseconds n 3 17 seconds 2 n 3. 7+E 64 centuries!! Nyhoff, ADTs, Data Structures and Problem Solving with C++, Second Edition, © 2005 Pearson Education, Inc. All rights reserved. 0 -13 -140909 -3 9