Algorithm Design Analysis Chapter 4 Mergesort Quicksort Counting

Algorithm Design & Analysis Chapter 4 : Mergesort Quicksort Counting sort 1

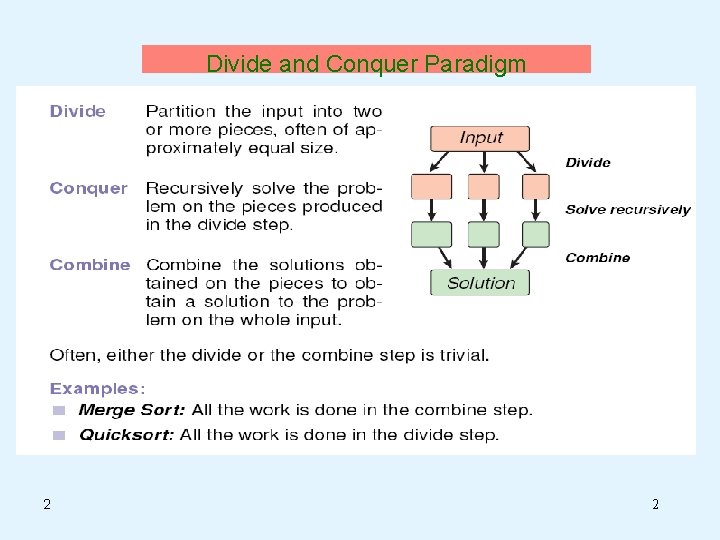
Divide and Conquer Paradigm 2 2

Algorithm Merge() Ø The procedure assumes that the subarrays A[p. . q] and A[q+1. . r] are in sorted order. Ø It merges them to form a single sorted subarray that replaces the current subarray A[p. . r]. Algorithm Merge(A, p, q, r) { n 1 : = q – p + 1; n 2 : = r – q; for i : = 1 to n 1 do L[i] : = A[p+i-1]; for j : = 1 to n 2 do R[j] : = A[q+j]; L[n 1+1] : = ∞; R[n 2+1] : = ∞; i : = 1; j : = 1; for k : = p to r do if (L[i] ≤ R[j]) then { A[k] : = L[i]; i : = i + 1; } else { A[k] : = R[j]; j : = j + 1; } } 3

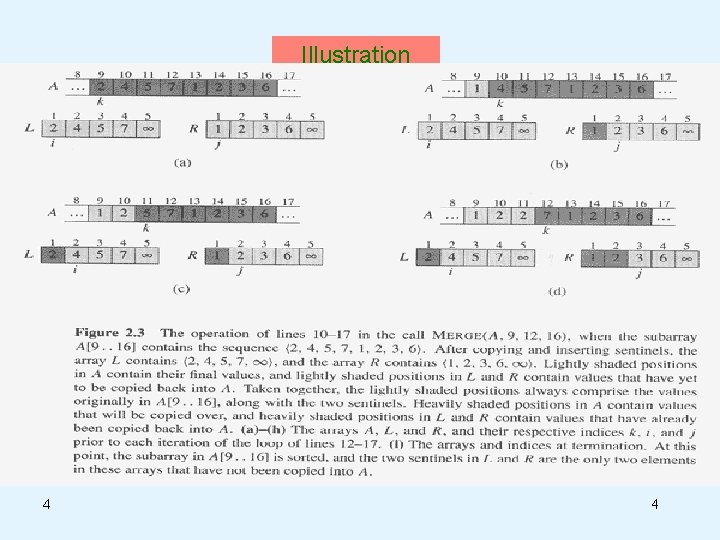
Illustration 4 4

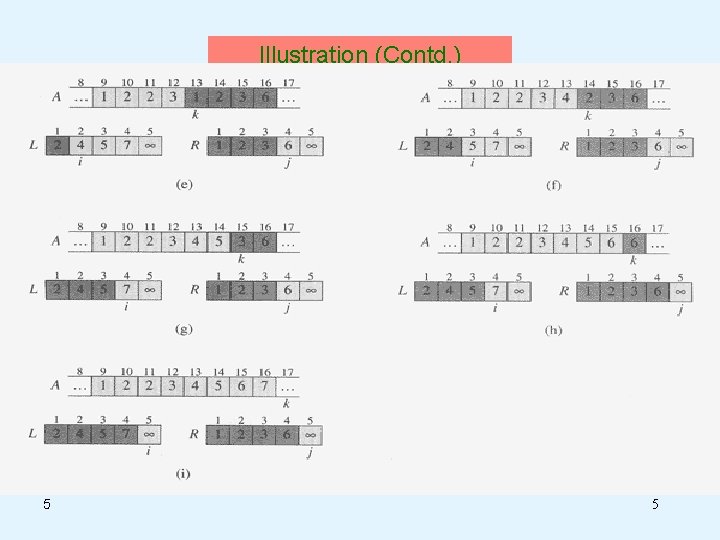
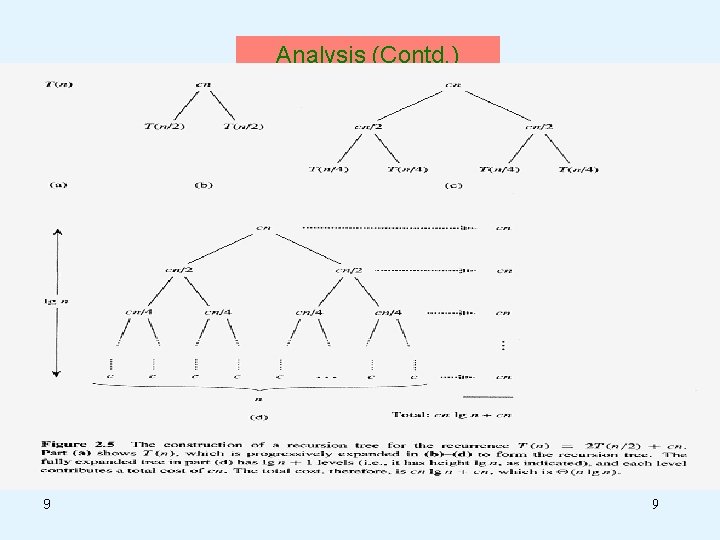
Illustration (Contd. ) 5 5

Merge Sort Ø The running time of Merge() is is Θ(n), where n = r – p + 1. Ø We can now use the Merge procedure as a subroutine in the merge sort algorithm. Ø The procedure Merge. Sort(A, p, r) sorts the elements in the subarray A[p. . q]. Ø If p ≥ r, the subarray has at most one element and is therefore already sorted. Ø Otherwise, the divide step simply computes an index q that partitions A[p. . r] into two subarrays: A[p. . q], containing elements, and A[q+1. . r], containing elements. 6 Algorithm Merge. Sort(A, p, r) { if (p < r) then { q : = (p+r)/2; Merge. Sort(A, p, q); Merge. Sort(A, q+1, r); Merge(A, p, q, r); } //floor of (p+r)/2 6

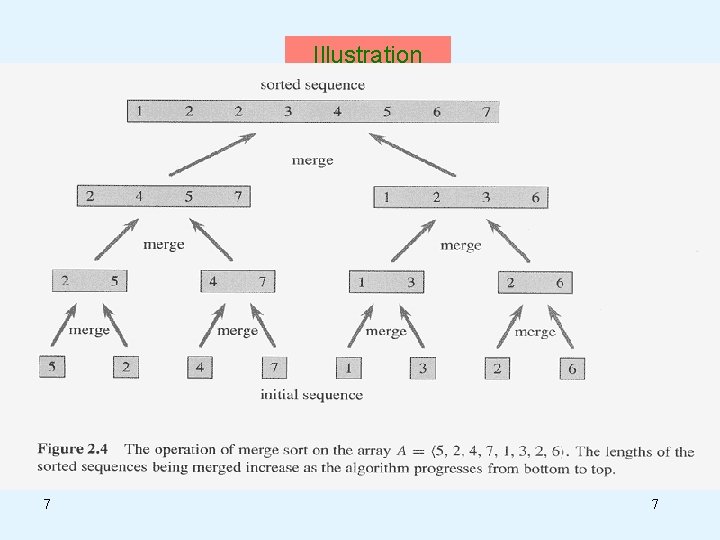
Illustration 7 7

Analysis of Merge Sort Ø Merge sort on just one element takes constant time. When we have n > 1 elements, we break down the running time as follows: Ø Divide: The divide step just compute the middle of the subarray, which takes constant time. Thus D(n)= Θ (1). Ø Conquer: We recursively solve two sub-problems, each of size n/2, which contributes 2 T(n/2) to the running time. Ø Combine: We have already noted that Merge procedure on an nelement sub-array takes time Θ(n), so C(n)= Θ(n). Ø Hence Ø By using Master Theorem, we get T(n)=Θ(n lg n). Ø We can prove by recursion-tree method also. Ø For that let us rewrite the recurrence as follows: 8 8

Analysis (Contd. ) 9 9

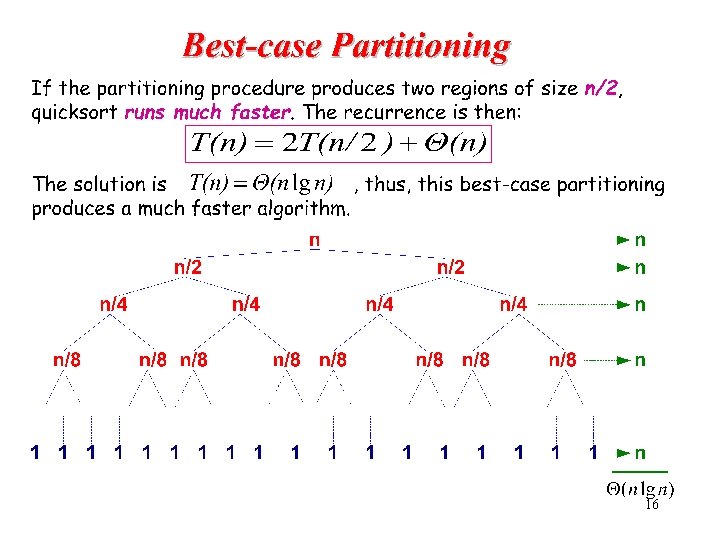
10

11

12

13

14

15

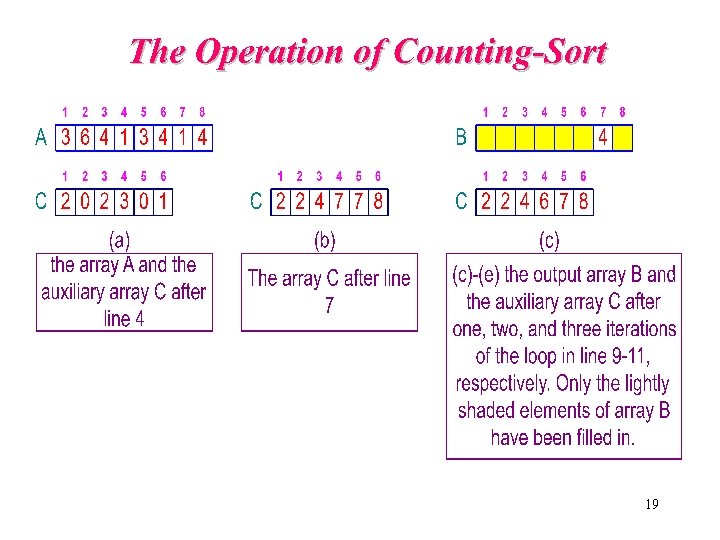
16

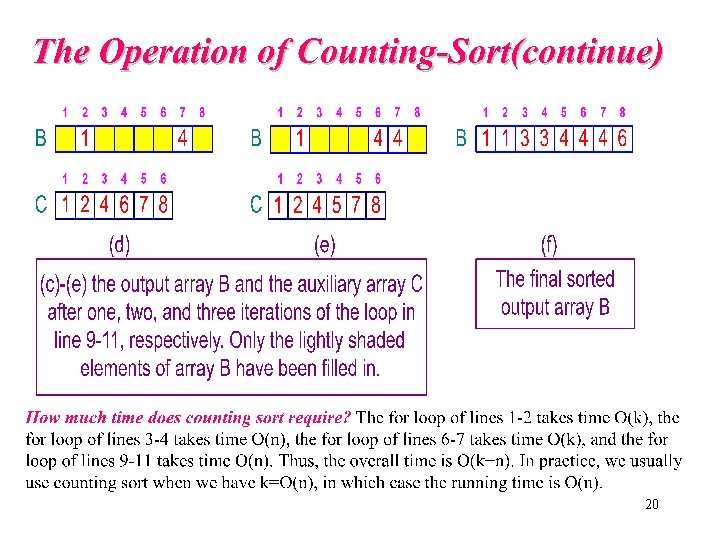
17

18

19

20