Algorithm analysis Input cases Analysing loops September 10

Algorithm analysis Input cases Analysing loops September 10, 2018 Cinda Heeren / Geoffrey Tien 1

Let's race! • September 10, 2018 Cinda Heeren / Geoffrey Tien 2

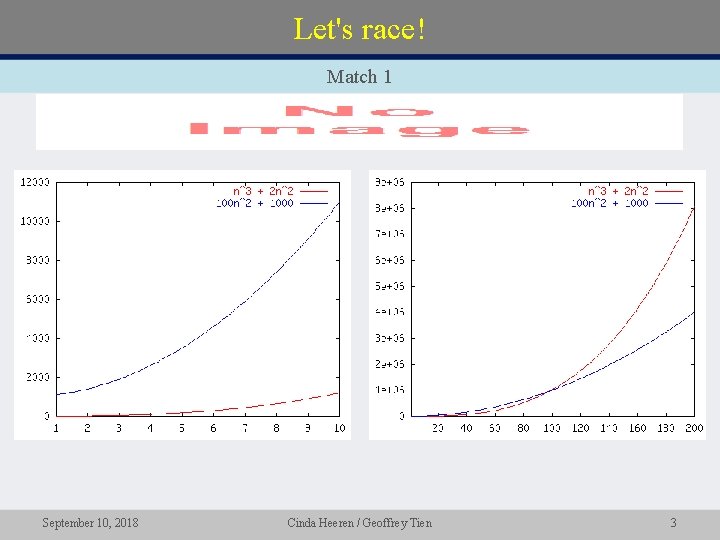
Let's race! Match 1 • September 10, 2018 Cinda Heeren / Geoffrey Tien 3

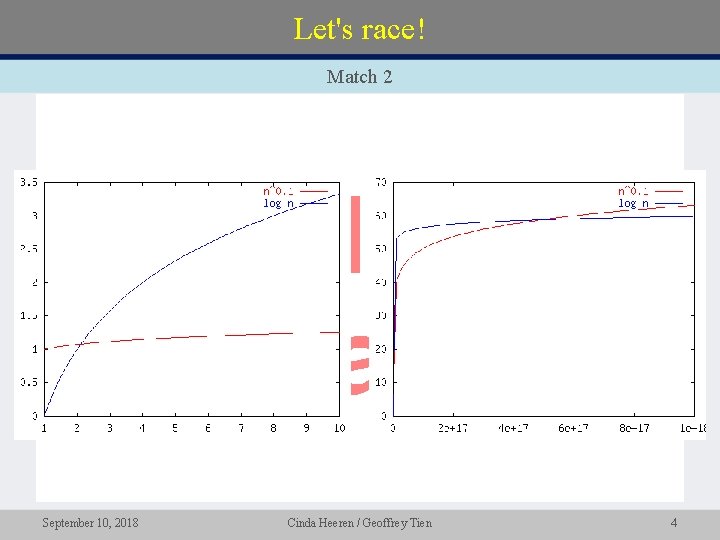
Let's race! Match 2 • September 10, 2018 Cinda Heeren / Geoffrey Tien 4

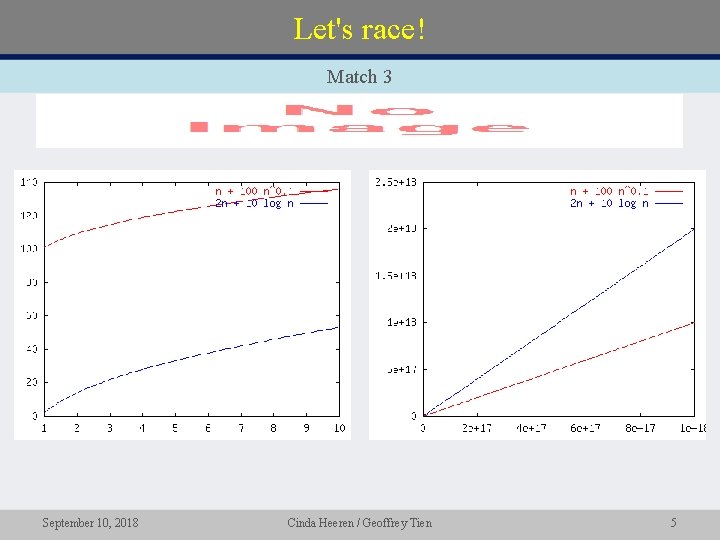
Let's race! Match 3 • September 10, 2018 Cinda Heeren / Geoffrey Tien 5

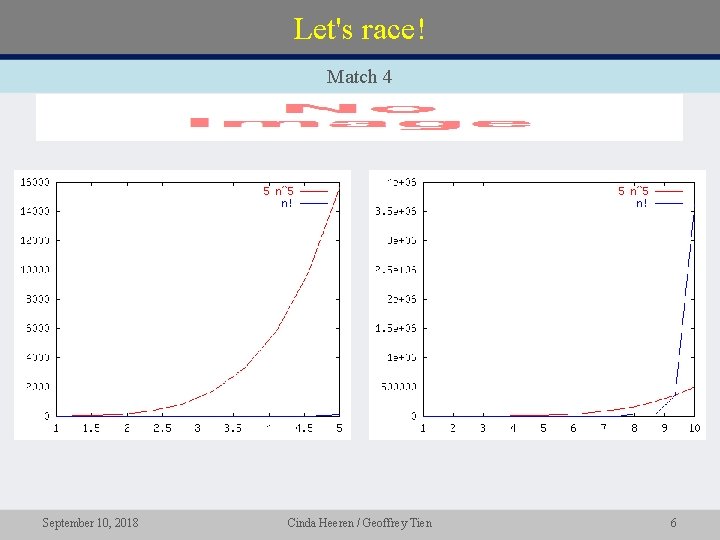
Let's race! Match 4 • September 10, 2018 Cinda Heeren / Geoffrey Tien 6

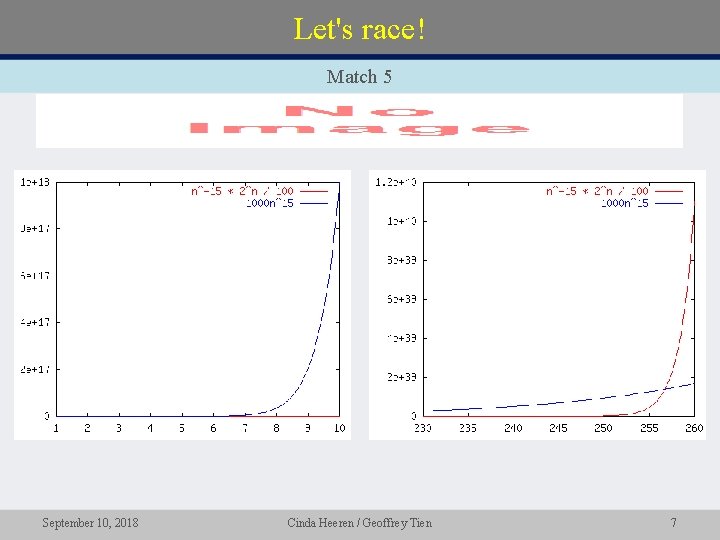
Let's race! Match 5 • September 10, 2018 Cinda Heeren / Geoffrey Tien 7

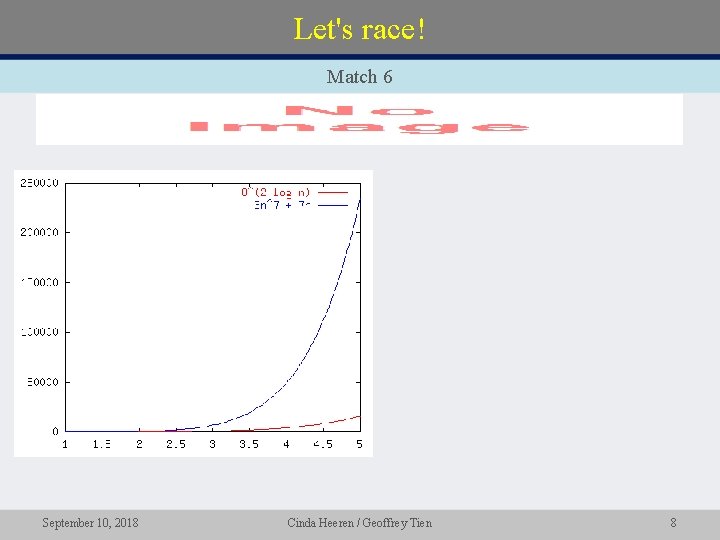
Let's race! Match 6 • September 10, 2018 Cinda Heeren / Geoffrey Tien 8

Let's race! Match 7 • September 10, 2018 Cinda Heeren / Geoffrey Tien 9

Let's race! Race results • September 10, 2018 Cinda Heeren / Geoffrey Tien 10

The match results were fixed! • September 10, 2018 Cinda Heeren / Geoffrey Tien 11

Dominance • September 10, 2018 Cinda Heeren / Geoffrey Tien 12

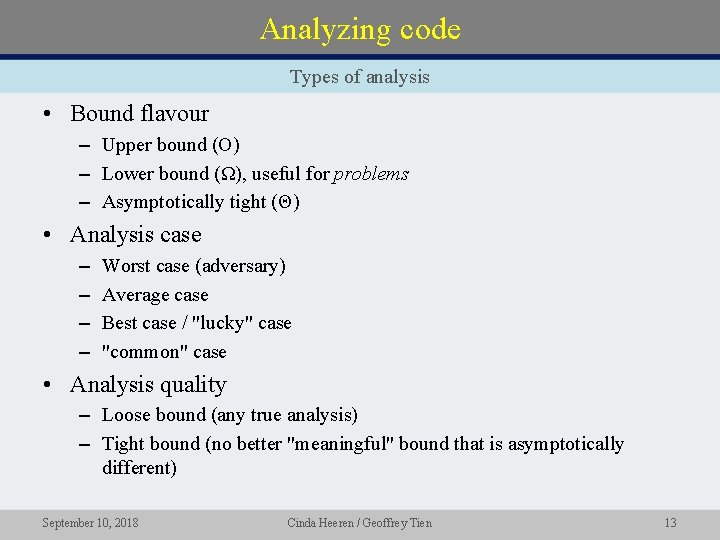
Analyzing code Types of analysis • Bound flavour – Upper bound (O) – Lower bound (Ω), useful for problems – Asymptotically tight (Θ) • Analysis case – – Worst case (adversary) Average case Best case / "lucky" case "common" case • Analysis quality – Loose bound (any true analysis) – Tight bound (no better "meaningful" bound that is asymptotically different) September 10, 2018 Cinda Heeren / Geoffrey Tien 13

Input varies • The number of operations usually varies based on the size of the input – Though not always – consider array lookup • In addition algorithm performance may vary based on the organization of the input – For example consider searching a large array – If the target is the first item in the array the search will be very fast September 10, 2018 Cinda Heeren / Geoffrey Tien 14

Linear Search // Iterative linear search int lin. Search(int arr[], int size, int x) { for (int i = 0; i < size; i++) { if (x == arr[i]) The function returns as { soon as a match is found return i; } } return -1; //target not found } -1 is returned if the target item is not found by the time the array end is reached September 10, 2018 Cinda Heeren / Geoffrey Tien 15

Linear search comparisons For different input organization • Worst case – The target is not in the array or – The target is at the last position in the array – Make n comparisons in either case • Best/lucky case (this rarely occurs) – The target is the first element of the array – Make 1 comparison • Average case – Is it (best case + worst case) / 2, i. e. (n + 1) / 2? – Average/usual case analysis is tricky and requires several assumptions that may not hold in all situations September 10, 2018 Cinda Heeren / Geoffrey Tien 16

Searching sorted arrays • September 10, 2018 Cinda Heeren / Geoffrey Tien 17

Binary search algorithm int bin. Search(int arr[], int size, int target) { int low = 0; int high = size - 1; int mid = 0; While subarray has at least 1 element while (low <= high) { mid = (low + high) / 2; if (target == arr[mid]) return mid; else if (target > arr[mid]) low = mid + 1; else //target < arr[mid] high = mid - 1; } return -1; //target not found } September 10, 2018 Cinda Heeren / Geoffrey Tien 18

Worst case Binary search • What is the worst case for binary search? – Either the target is not in the array, or – It is found when the search space consists of one element • How many times does the while loop iterate in the worst case? bin. Search(arr, n, 64); mid = (0+15) / 2 = 7 mid = (8+15) / 2 = 11 mid = (8+10) / 2 = 9 mid = (10+10) / 2 = 10 Done 7 11 15 21 29 32 44 45 57 61 64 73 79 81 86 92 0 1 2 3 4 5 6 8 10 11 12 13 15 September 10, 2018 7 9 Cinda Heeren / Geoffrey Tien 14 19

Worst case analysis Binary search • September 10, 2018 Cinda Heeren / Geoffrey Tien 20

Average case Binary search • Is the average case more like the best case or the worst case? – What is the chance that an array element is the target • 1/n the first time through the loop • 1/(n/2) the second time through the loop • … and so on … • It is more likely that the target will be found as the search space becomes small – That is, when the while loop nears its final iteration – We can conclude that the average case is more like the worst case than the best case September 10, 2018 Cinda Heeren / Geoffrey Tien 21

Analysing nested loops • Generally, we count the number of times an inner loop is repeated, for each time an outer loop is executed – e. g. a function which scans an array looking for duplicates, worst case bool has. Duplicate(int arr[], int size) { for (int i = 0; i < size-1; i++) { for (int j = i+1; j < size; j++) { if (arr[i] == arr[j]) return true; } } return false; } September 10, 2018 Cinda Heeren / Geoffrey Tien 22

Analysing nested loops has. Duplicate, worst case bool has. Duplicate(int arr[], int size) { for (int i = 0; i < size-1; i++) { for (int j = i+1; j < size; j++) { if (arr[i] == arr[j]) return true; } } return false; } # of inner loop executions 0 1 2. . . 1 # of inner loop executions September 10, 2018 Cinda Heeren / Geoffrey Tien 23

How the loop variable changes • The loop variables here does not increment in the usual way – Then how many times is the loop body executed? void candyapple(int n) { for (int i = 1; i < n; i *= 3) cout << "iteration: " << i << endl; } void caramelcorn(int n) { for (int i = 0; i * i < 6 * n; i++) cout << "iteration: " << i << endl; } September 10, 2018 Cinda Heeren / Geoffrey Tien 24

Readings for this lesson • Carrano & Henry – Chapter 10 (Algorithm efficiency) • Next class: Proof by induction – Epp: Chapter 5. 2 – 5. 3 – Review: Epp Chapter 4, 5. 1 September 10, 2018 Cinda Heeren / Geoffrey Tien 25