Algorithm Analysis How Do We Determine the Complexity

Algorithm Analysis How Do We Determine the Complexity of Algorithms Rosen 3. 3 Creative Commons License – Curt Hill

Two Flavors of Complexity • Time and Space • Time complexity deals with how many instructions need to be executed based on the number of inputs • Space complexity deals with how much memory is required, also based on number of inputs – This is dependent on the data structures used – Book will not discuss this one Creative Commons License – Curt Hill

Time Complexity • We typically focus on one or several types of instructions • These may be any of the following types: – Comparisons – Assignment statements Creative Commons License – Curt Hill

Why These? • There is considerable difference in the speeds of these instructions over expenses of various computers • Moreover, there may be other support instructions that may be present or absent depending on the machine language used • Yet these factors generally get rolled into the constants in Big O and similar notations Creative Commons License – Curt Hill

Max of Sequence • procedure max(a 1, a 2, …an: integer) max : = a 1 {Assignment on name} for i=2 to n if max < ai then max : = ai return max {All done} • There is an obvious and a subtle comparison • Similarly there are obvious assignments and subtle Creative Commons License – Curt Hill

Analysis • For comparisons – N-1 comparisons in the if – The for uses N compares on whether i has reached its limit – Thus 2 N – 1 comparisons • Assignments is harder for it varies – Best case, first is max, just 1 – Worst case, list is in ascending order N – Average case, N/2 • We would call this O(N) Creative Commons License – Curt Hill

Bubble procedure bubble(a 1, a 2…an: integer) swapped: Boolean n: integer do swapped : = false for j : = 1 to n-1 if aj < aj+1 temp : = aj aj : = aj+1 : = temp swapped : = true n : = n – 1 until not swapped Creative Commons License – Curt Hill

Commentary • This bubble sort is slightly better than that given in Rosen • The largest element always sinks to the bottom, so why check it again? – This is the n: =n-1 • It also stops sorting when there are no interchanges • However, these do complicate the analysis Creative Commons License – Curt Hill

Inner loop contents • Inside the inner loop there will be two comparisons – One for loop, one for if • Zero or four assignments • 1 increment of control variable Creative Commons License – Curt Hill

How many loops? • Creative Commons License – Curt Hill

• Cases Creative Commons License – Curt Hill

Commentary • Typically sorts fall into three big O categories • O(n 2) – bad sorts – Bubble, selection, insertion and others • O(n log n) – good sorts – Quick, Heap, Merge • Weird cases – Shell O(n~1. 25) Creative Commons License – Curt Hill

Tractable and not • Algorithms with explosively growing Big Os are called intractable • Polynomial and slower growing are tractable – Algorithms with exponents larger than four are unusual • Exponential, factorial and faster growing algorithms are generally intractable Creative Commons License – Curt Hill

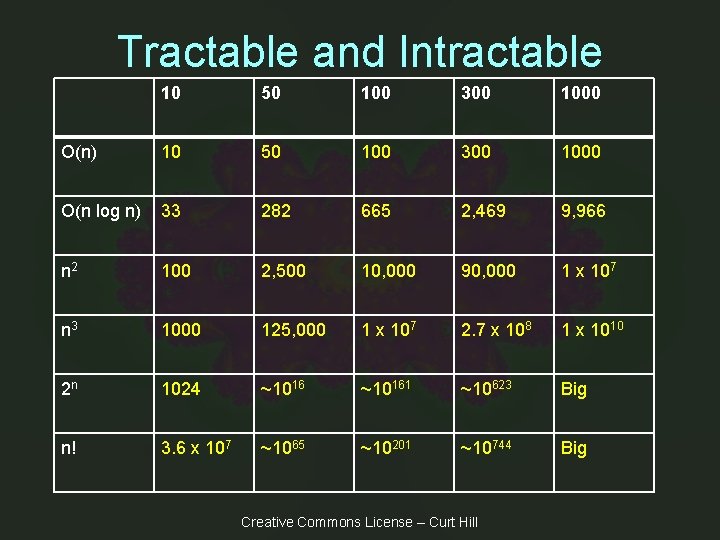
Tractable and Intractable 10 50 100 300 1000 O(n) 10 50 100 300 1000 O(n log n) 33 282 665 2, 469 9, 966 n 2 100 2, 500 10, 000 90, 000 1 x 107 n 3 1000 125, 000 1 x 107 2. 7 x 108 1 x 1010 2 n 1024 ~10161 ~10623 Big n! 3. 6 x 107 ~1065 ~10201 ~10744 Big Creative Commons License – Curt Hill

Worst and Average • There are instances of problems where worst case estimates are intractable, but average cases are not • We typically attempt to solve these, but if the program runs longer than desired we quit • In problems that we know are intractable we may have to settle for an approximate solution Creative Commons License – Curt Hill

P and NP • Those problems with known solutions belong to a class labeled P • There is also a class of problems labeled NP which are believed to have intractable solutions, but if a solution is known it can be checked in polynomial time • There is also the NP complete set of problems – If any of them can be solved in polynomial time then all of them can be solved in polynomial time Creative Commons License – Curt Hill

Traveling Salesman Problem • Given a set of cities with distances between them • Find the shortest route that visits each city exactly once and returns to the city of origin • Variations are NP-Complete with others being even worse NP-Hard Creative Commons License – Curt Hill

Knapsack Problem • Given various articles of different weights and volumes • Find the set which has a weight less than some maximum with the greatest volume Creative Commons License – Curt Hill

Bin Packing Problem • Given a set bins of a given volume • Pack a set of items which are of differing volumes into a minimum number of bins • If the number of bins is restricted to one this becomes the knapsack problem Creative Commons License – Curt Hill

Worse than intractable? • The halting problem show us that there also unsolvable problems • Clearly worse than intractable Creative Commons License – Curt Hill

Exercises • 3. 3 – 3, 7, 11, 17, 23 Creative Commons License – Curt Hill