Algebraically Finiding an Equation of a Line with

Algebraically Finiding an Equation of a Line with a Point and Slope

Algebraically Finding the y-intercept Colleen wants to know how much a chick weighs when it is hatched. Colleen tracked one of her chickens and found it grew steadily by about 5. 2 grams each day since it was born. Nine days after it hatched, the chick weighed 98. 4 grams. Algebraically determine how much the chick weighed the day it was hatched. When the chick was hatched, it was day 0. Thus, we need to find the y-intercept. Since the growth is constant, the situation in linear: The growth (slope) is 5. 2 grams per day The chick weighed 98. 4 grams (y) after 9 days (x) 51. 6 grams The equation now has one distinct variable. Solve it.

Algebraically Finding a x-Value Now Colleen wants to know when the chicken will weigh 140 grams. Algebraically find the answer. Use the slope and y-intercept to write an equation. Use the Slope. Intercept form: The 140 grams represents a y value. The equation now has one distinct variable. Solve it. Substitute 140 for y 17 Days

Example Algebraically find the equation for a line with a slope of -3, passing through the point (15, -50). Find the y-intercept. Use Slope-Intercept Form: The slope is -3 A point on the graph is x=15 and y=-50 The equation now has one distinct variable. Solve it. Substitute back into Slope. Intercept Form:

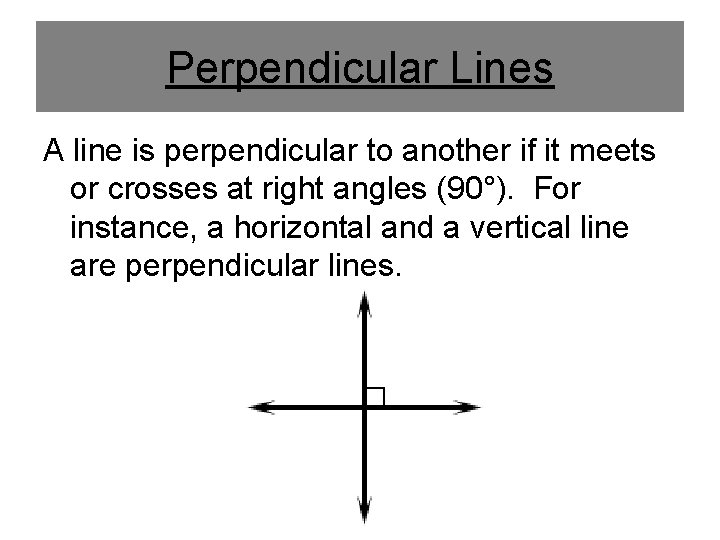
Perpendicular Lines A line is perpendicular to another if it meets or crosses at right angles (90°). For instance, a horizontal and a vertical line are perpendicular lines.

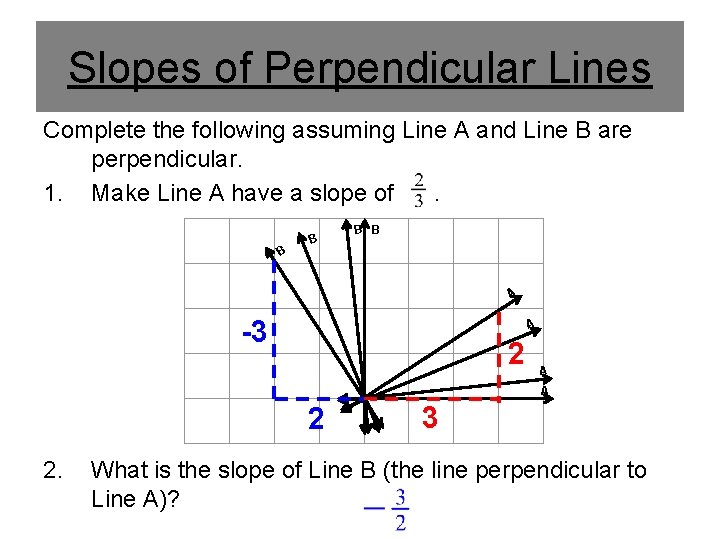
Slopes of Perpendicular Lines Complete the following assuming Line A and Line B are perpendicular. 1. Make Line A have a slope of. B B A -3 A 2 A A 2 2. 3 What is the slope of Line B (the line perpendicular to Line A)?

Slopes of Perpendicular Lines Two lines are perpendicular if their slopes are opposite reciprocals of each other. In other words, if the slope of a line is then the perpendicular line has a slope of. Example: What is the slope of a line perpendicular to each equation below.

Example Algebraically find the equation of the line that goes through the point (2, 3) and is perpendicular to y = -4 x – 2. This y-intercept does not matter. Find the y-intercept. Use Slope-Intercept Form: The slope is ¼ A point on the graph is x=2 and y=-3 The equation now has one distinct variable. Solve it. Substitute back into Slope. Intercept Form:

Example: Parallel Lines Algebraically find the equation of the line that goes through the point (16, 4) and is parallel to 3 x + 4 y = 8. Find the Slope Find the y-intercept. Use Slope. Intercept Form: A point on the graph is x=16 and y=4 Since Parallel Lines have the same slope, our new equation also has slope -3/4. (This yintercept does not matter) Substitute back into Slope-Intercept Form: The slope is -3/4 The equation now has one distinct variable. Solve it.