ALGEBRAIC STRUCTURE Coset Normal Subgroup Group Homomorphism Lecturer

ALGEBRAIC STRUCTURE: Coset, Normal Subgroup, Group Homomorphism Lecturer— 5 -6 ALGEBRAIC STRUCTURE Dr. Prasant Kumar Nayak

Coset

Coset What about H+3, H+4, H+5……. . Note: In abelian group each left coset equal to right coset.

Properties of cosets: (Home work) Proof the following

Lagrange's Theorem •

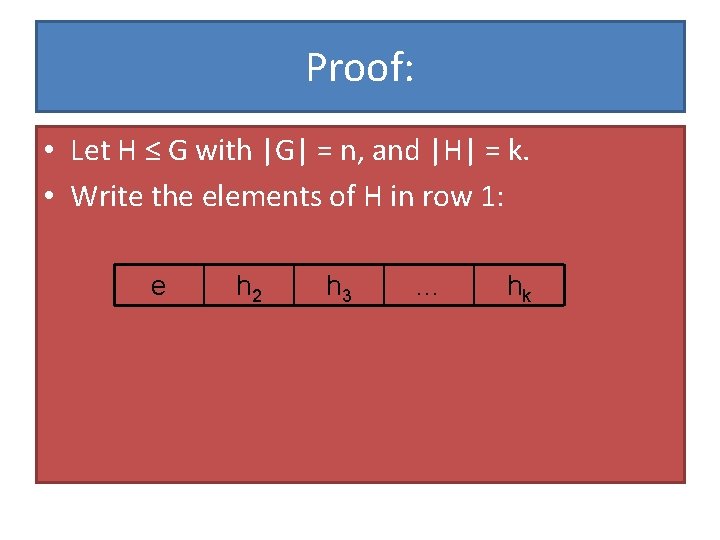
Proof: • Let H ≤ G with |G| = n, and |H| = k. • Write the elements of H in row 1: e h 2 h 3 … hk

Proof: • Choose any a 2 in G not in row 1. • Write a 2 H in the second row. e a 2 h 2 h 3 a 2 h 3 … … hk a 2 hk

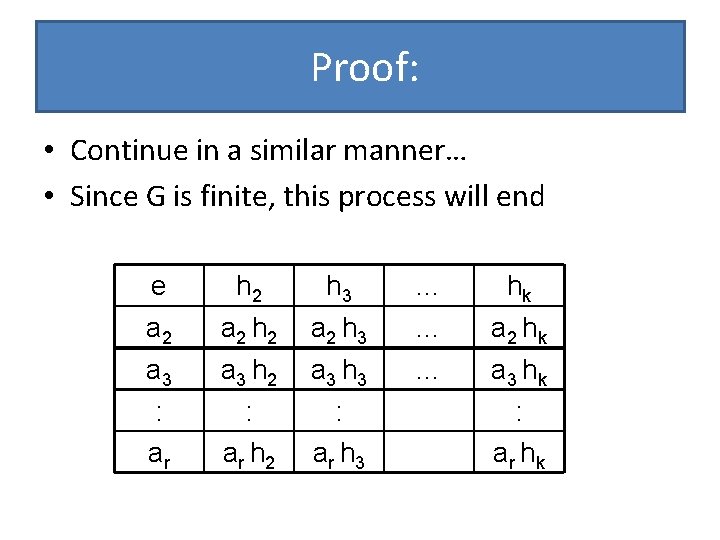
Proof: • Continue in a similar manner… • Since G is finite, this process will end e a 2 h 2 h 3 a 2 h 3 … … hk a 2 hk a 3 : ar a 3 h 2 : ar h 2 a 3 h 3 : ar h 3 … a 3 hk : ar hk

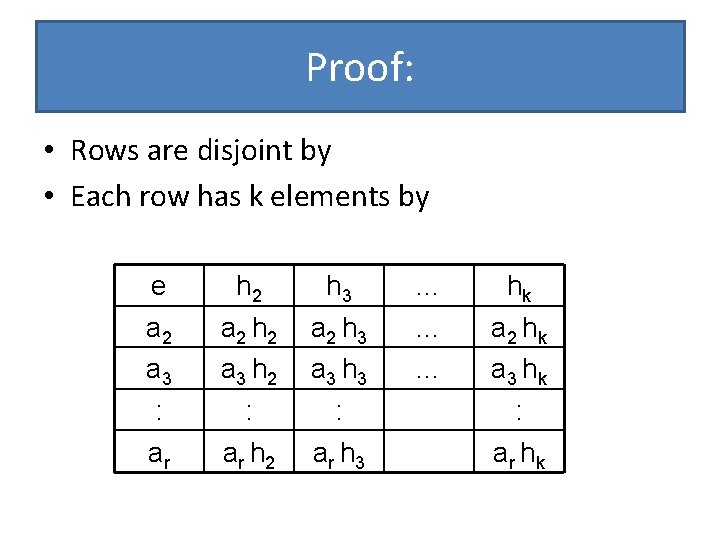
Proof: • Rows are disjoint by • Each row has k elements by e a 2 a 3 : ar h 2 a 2 h 2 a 3 h 2 : ar h 2 h 3 a 3 h 3 : ar h 3 … … … hk a 2 hk a 3 hk : ar hk

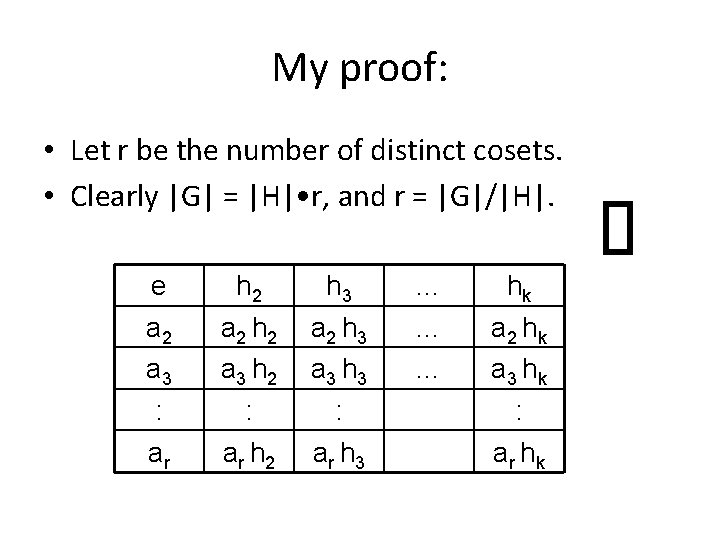
My proof: • Let r be the number of distinct cosets. • Clearly |G| = |H| • r, and r = |G|/|H|. e a 2 a 3 : ar h 2 a 2 h 2 a 3 h 2 : ar h 2 h 3 a 3 h 3 : ar h 3 … … … hk a 2 hk a 3 hk : ar hk

Normal subgroups • Definition 18：A subgroup H of a group is a normal subgroup if g. H=Hg for g G. • Example: Any subgroups of Abelian group are normal subgroups.

Normal subgroups •

Homomorphism of Group •