Algebraic Reflections of Topological Reality An informal introduction

Algebraic Reflections of Topological Reality An informal introduction to algebraic homotopy theory

Topology A topological space is a set X together with a collection T of subsets of X that are deemed to be open. The collection T must satisfy certain axioms. Example: X = R (the real line) T = { unions of open intervals }

Topology A couple of attractive topological spaces…

Topology A continuous map from (X, T ) to (Y, U ) is a function f: X Y such that the pre-image of any open set of Y is an open set of X. Example: f(x)= sin x-3 cos x is a continuous map from R to R.

Homotopy = continuous deformation Allowed: shrinking, stretching, bending Forbidden: cutting and pasting Angles and distances are NOT preserved!
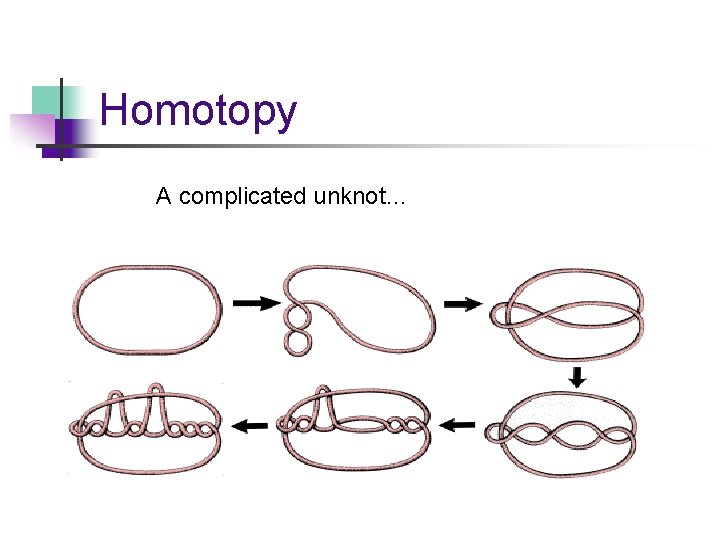
Homotopy A complicated unknot…
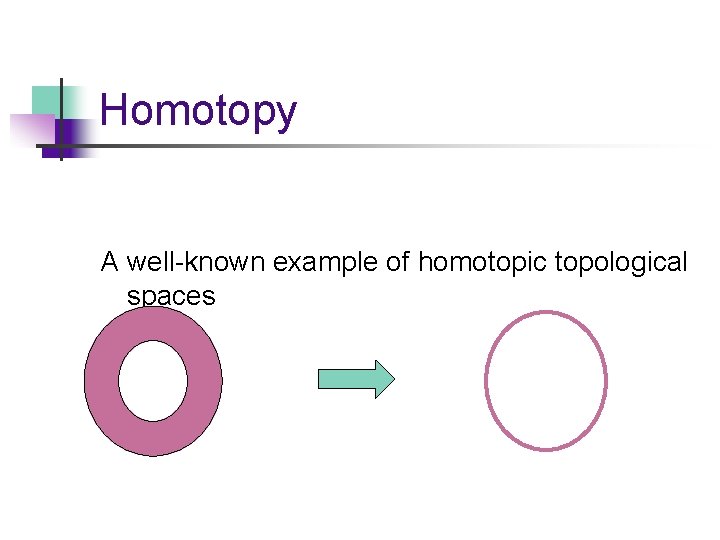
Homotopy A well-known example of homotopic topological spaces
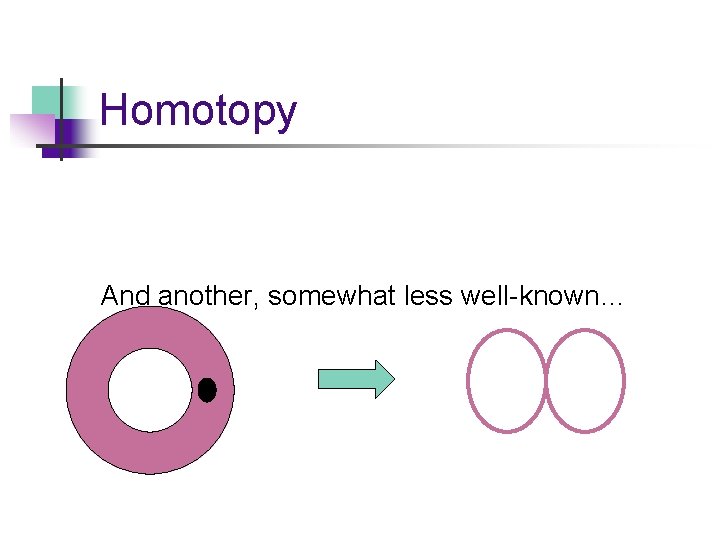
Homotopy And another, somewhat less well-known…

Homotopy invariants H : {topological spaces} {algebraic gadgets} such that if (X, T) homotopic to (Y, U), then H(X, T)=H(Y, U). Example: the number of holes in a surface is a homotopy invariant (coffee cups and donuts…)

Homotopy invariants Warning! In general, H(X, T)=H(Y, U) does NOT imply that (X, T) is homotopic to (Y, U). The better a homotopy invariant is at distinguishing between topological spaces that are not homotopic, the harder it is to calculate.

Algebraic models Topological spaces & Continuous maps F Algebraic gadgets & Their special maps The algebraic gadgets are “sets with extra structure” (e. g. , vector spaces) and their “special maps” are functions preserving this extra structure (e. g. , linear transformations).

Algebraic models Topological spaces & Continuous maps F Algebraic gadgets & Their special maps We work with algebraic gadgets for which there is a reasonable notion of “homotopy” of their special maps.
Algebraic models Topological spaces & Continuous maps F Algebraic gadgets & Their special maps F is an algebraic model of topological spaces if F(X, T) and F(Y, U) are homotopic whenever (X, T) and (Y, U) are homotopic.

My research Developing new, more precise algebraic models that capture as much homotopy information as possible, while remaining calculable.

My research Using new and known models to solve topological problems, similar to: (X, T) (Z, V) (Y, U) ?

My research Applying new and known algebraic models to solving problems in concurrency theory, e. g. , to the classification of transition systems and higher dimensional automata.
- Slides: 16