Algebraic Method of Solving the Linear Harmonic Oscillator

Algebraic Method of Solving the Linear Harmonic Oscillator Lecture by Gable Rhodes PHYS 773: Quantum Mechanics February 6 th, 2012

Simple Harmonic Oscillator • Many physical problems can be modeled as small oscillations around a stable equilibrium • Potential is described as parabolic around the minimum energy • The Hamiltonian is formulated in the usual way for canonical variables q and p. Gable Rhodes, February 6 th, 2012 2

Raising & Lowering Operators - Defined • After substituting in our potential, we can rearrange the constants slightly to give the Hamiltonian a more suggestive appearance • If we “factor” the operators, we get • Recognizing that the last term is the commutator of the canonical variables, we get Gable Rhodes, February 6 th, 2012 3

Raising & Lowering Operators - Defined • We can now define the operator a • Upon substitution • And Simplifying Gable Rhodes, February 6 th, 2012 4

Raising & Lowering Operators - Defined • If we reverse the order of the operators, a similar expression is obtained • Subtracting the two forms yields the commutator • Simplifying to Gable Rhodes, February 6 th, 2012 5

Raising & Lowering Operators - Defined • It is important to note that the a, a† operators are defined in such a way that as long as the state variables follow the canonical commutation relation, the a, a† commutator will be 1. • And the Hamiltonian can be written as a linear function of a, a† Gable Rhodes, February 6 th, 2012 6

Properties of a, a† • If a wave function has the property that it is an eigenfunction of the Hamiltonian • We can introduce the equivalent statement for the operator aa† with generic eigenvalue, λ • We then apply the a† operator to a†ψ and test if the result is the same eigenvector. Use commutator Gable Rhodes, February 6 th, 2012 7

Properties of a, a† • And the equivalent method for a • Using the relationship of Hamiltonian, we can then relate eigenvalues Gable Rhodes, February 6 th, 2012 8

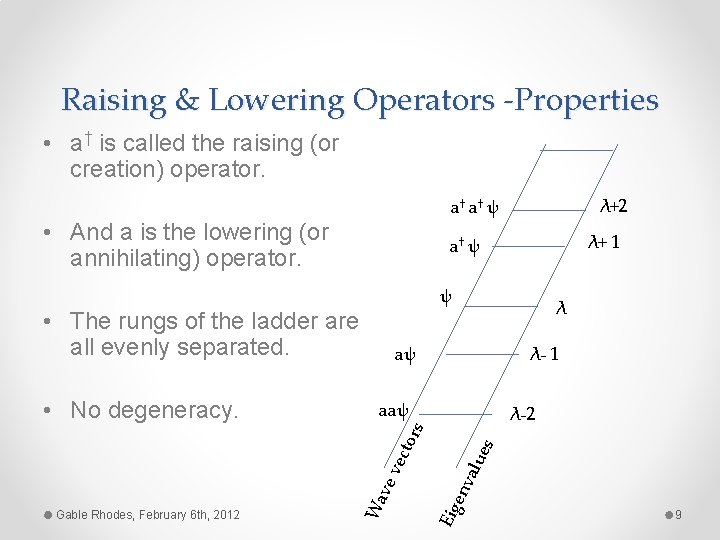
Raising & Lowering Operators -Properties • a† is called the raising (or creation) operator. • And a is the lowering (or annihilating) operator. ψ λ aψ λ- 1 aaψ λ-2 Eig env alu es tor s vec ve Wa Gable Rhodes, February 6 th, 2012 λ+ 1 a† ψ • The rungs of the ladder are all evenly separated. • No degeneracy. λ+2 a† a† ψ 9

What is the Significance? • If we have any solution, we can find infinitely more solutions by repeated application of the raising and lowering operators • But, importantly, although there are infinite solutions we know that the are no solutions with negative energy (both kinetic and potential components for the Hamiltonian are always positive) • Therefore, a ground state must exist. (this is also a property of Sturm-Liouville PDE) • Applying the lowering operator to the ground state will result in a null vector (trivial state). • Eq. 10 -77 Gable Rhodes, February 6 th, 2012 10

Raising & Lowering Operators -Eigenvectors • Once we have a ground state, repeated application of the raising operator will result in an infinite set of eigenvectors with distinct (non-degenerate) eigenvalues. • And introducing an arbitrary starting point λ 0. • But for the special case of the ground state • Must be zero on the right side (by our definition), so λ 0 is exactly 0. Gable Rhodes, February 6 th, 2012 11

Determine the Energy Levels • Using the previous equation relating the Hamiltonian and aa†, we can relate energy to λ (n). • And since we started at the ground state, we can relate the energy level to the eigenvectors • If we use a normalization constant • Where An can be found by direct integration at each step or by algebraic tricks (later) Gable Rhodes, February 6 th, 2012 12

What Are These Operators Good For Anyway? • We found Energy exactly and wavevectors in abstract form. • What else can we do with them? • What about expectation values? In chapter 5, problem 2, we were asked to find <V>. This required direct integration with the (explicitly known) wavefunction. • Can this be done without knowing the wavefunction? Gable Rhodes, February 6 th, 2012 13

Expectation value of Potential • If we use the definition of a†, a and rewrite q and p operators in terms of a and a† we get • Now these can be substituted into <V> Gable Rhodes, February 6 th, 2012 14

Expectation value of Potential • Of the four terms in the integral, we see that two of them vanish due to the orthogonality of the wavevectors. • And the other two are known to us from the previous work. Gable Rhodes, February 6 th, 2012 15

Expectation value of Potential • This makes the result pretty straightforward • And the this result agrees with problem 5. 2, and the virial theorem • But, we did not need to know the explicit form of the wavefunction. Gable Rhodes, February 6 th, 2012 16

<q>, <p>, <q 2>, <p 2> • Other key expectation values can be easily obtained. Gable Rhodes, February 6 th, 2012 17

Variance and Uncertainty? • The variance is therefore • And this agrees with the uncertainty principle Gable Rhodes, February 6 th, 2012 18

What is left then? • The Normalization constant, which can also be determined algebraically. • Square both sides and integrate • After integration by parts and throwing out the boundary terms. • So that gives us our wavefunction in terms of the ground state and raising operator Gable Rhodes, February 6 th, 2012 19

Normalization • Lets try ψ1. • Next try ψ2. • We can now write the general equation Gable Rhodes, February 6 th, 2012 20

And what is ψ0? • Starting with our condition for the ground state • And using the definition of the operator • We get a first order ODE Gable Rhodes, February 6 th, 2012 21

And what is ψ0? • The equation is separable and easily solved. • After normalization we get • Which is consistent with the solutions in chapter 5. Gable Rhodes, February 6 th, 2012 22

Finding ψ1. • Here we can use the raising operator to generate further solutions • Substitute in the operator • After rearranging, we get the desired result. Gable Rhodes, February 6 th, 2012 23

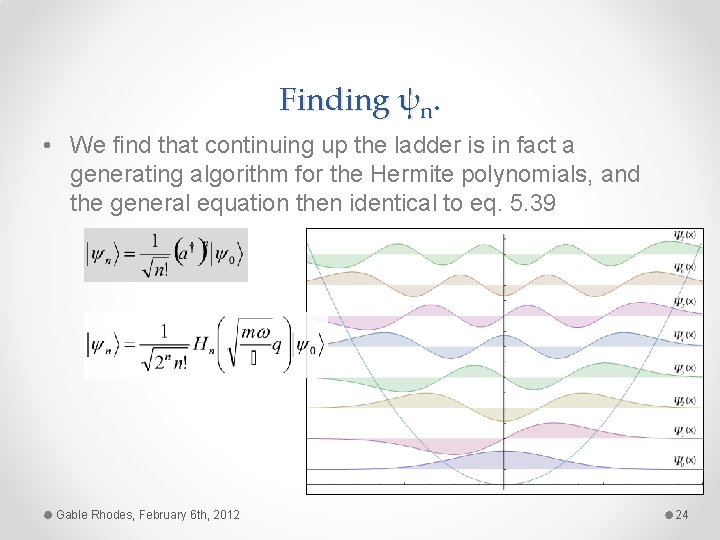
Finding ψn. • We find that continuing up the ladder is in fact a generating algorithm for the Hermite polynomials, and the general equation then identical to eq. 5. 39 Gable Rhodes, February 6 th, 2012 24

Matrix representation of a, a† • We can show that the lowering operator relates neighboring wave vectors with the normalization factor. • Adding the bra. • This gives the matrix elements of a as shown. Gable Rhodes, February 6 th, 2012 25

Matrix representation of a, a† • As an example, lowering n=2, Gable Rhodes, February 6 th, 2012 26

Matrix representation of a, a† • The equivalent representation of the raising operator is derived from the expression • Adding the bra. Gable Rhodes, February 6 th, 2012 27

Matrix representation of a, a† • With the lowering and raising operators in matrix form, we can then solve for the q and p operators in terms of a, a †. • For position we get, Gable Rhodes, February 6 th, 2012 28

Matrix representation of a, a† • And the equivalent expression for momentum is, • The complex constant insures that the anti-symmetric matrix is Hermitian. Gable Rhodes, February 6 th, 2012 29