Algebraic Graph Algorithms a little algebra goes a

Algebraic (Graph) Algorithms (a little algebra goes a long way) Jesper Nederlof NETWORKS training week ‘ 19 Asperen

(Preliminary) Outline • Addition and Multiplication • Linear Algebra • (Bipartite) Perfect Matchings • Short paths (`assignment problem’) • Cliques • Set Cover • Steiner Trees • Finding Long Paths • Finding (short) Hamiltonian cycles (`Traveling Salesman Problem’) • If time left: A simple Probabilistically Checkable Proof for NP

Algebraic Algorithms •

Arithmetic on primary school 0001100 23958233 5830 + -----23964063 23958233 5830 × -------0000 (=23, 958, 233× 0) 71874699 (=23, 958, 233× 30) 191665864 (=23, 958, 233× 800) 119791165 + (=23, 958, 233× 5, 000) ------139676498390 (=139, 676, 498, 390)

Arithmetic on primary school 0001100 23958233 5830 + -----23964063 23958233 5830 × -------0000 71874699 191665864 119791165 + -------139676498390

Arithmetic on primary school 0001100 23958233 5830 + -----23964063 23958233 5830 × -------0000 71874699 191665864 119791165 + -------139676498390

Arithmetic on primary school 0001100 23958233 5830 + -----23964063 23958233 5830 × -------0000 71874699 191665864 119791165 + -------139676498390

Arithmetic on primary school 0001100 23958233 5830 + -----23964063 23958233 5830 × -------0000 71874699 191665864 119791165 + -------139676498390

Arithmetic on primary school 0001100 23958233 5830 + -----23964063 23958233 5830 × -------0000 71874699 191665864 119791165 + -------139676498390

High school: complex numbers • (a+bi)*(c+di) = (ac-bd)+(ad+bc)i • Given a, b, c, d, compute (ac-bd) and (ad+bc). • How many multiplications are needed? • Only three! Try to find them if you want. . . – Use M 1 = ac, M 2=bd, M 3=…. . – Then (ac-bd) = M 1 -M 2 (ad+bc) = M 3 -ac-bd = M 3 -M 1 -M 2

High school: complex numbers • (a+bi)*(c+di) = (ac-bd)+(ad+bc)i • Given a, b, c, d, compute (ac-bd) and (ad+bc). • How many multiplications are needed? • Only three! Try to find them if you want. . . – Use M 1 = ac, M 2=bd, M 3=(a+b)(c+d). – Then (ac-bd) = M 1 -M 2 (ad+bc) = M 3 -ac-bd = M 3 -M 1 -M 2

How fast can we multiply integers, really? •

How fast can we multiply integers, really? •

Karatsuba There is a long history in complexity theory where guesses of the form “The obvious algorithm is optimal” have failed.

How fast can we multiply integers, really? •

polynomials How fast can we multiply integers, really? • - - -

How fast can we multiply integers, really? •
![Network Coding Conjecture [Li&Li’ 04]: The coding rate is never better than the multi-commodity Network Coding Conjecture [Li&Li’ 04]: The coding rate is never better than the multi-commodity](http://slidetodoc.com/presentation_image_h2/a4bddc93db11d81970c3b74f6ddc8ed1/image-18.jpg)
Network Coding Conjecture [Li&Li’ 04]: The coding rate is never better than the multi-commodity flow rate, in undirected graphs.
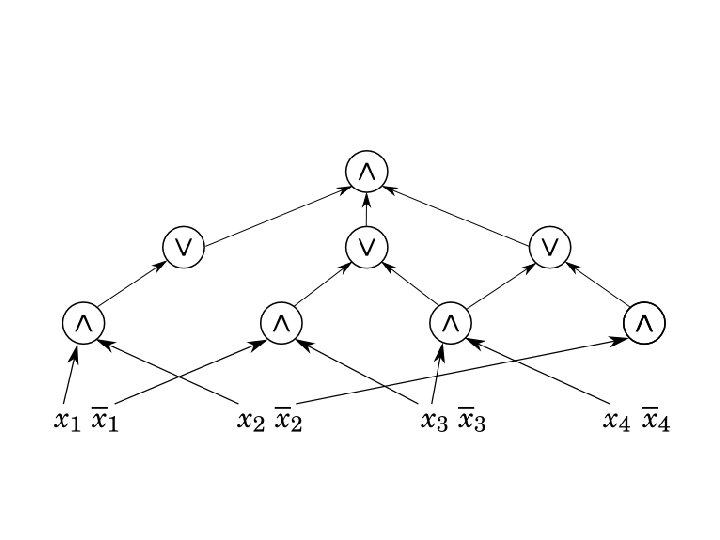

Addition (Subset Sum)

Subset Sum • Given: integers • Asked: is there and integer such that NP-complete!

Subset Sum • Given: integers • Asked: is there and integer such that NP-complete! Example {1 2 3 4 5 6 7 8 9 10 11 12}, = 50

Subset Sum • Given: integers • Asked: is there and integer such that NP-complete! Example {1 2 3 4 5 6 7 8 9 10 11 12}, = 50

• Subset Sum 3 20 58 90 267 493 869 961 1000 1153 1246 1598 1766 1922

• Subset Sum 3 20 58 90 267 493 869 961 1000 1153 1246 1598 1766 1922

Dynamic Programming (DP) • Initiated in 1950's by Bellman in his book "Bottleneck Problems and Dynamic Programming" • Nowadays one of most prominent algorithmic techniques in designing algorithms. • Discussed in any basic course or text book on algorithms

Dynamic Programming (DP) • The method works with a big table of data that has to be stored in the (preferably working) memory • A relatively easy procedure computes new table entries using already computed table entries • This easy procedure is often so easy that we just write it down as a single formula, obtaining a recurrence.

• Subset Sum 3 20 58 90 267 493 869 961 1000 1153 1246 1598 1766 1922
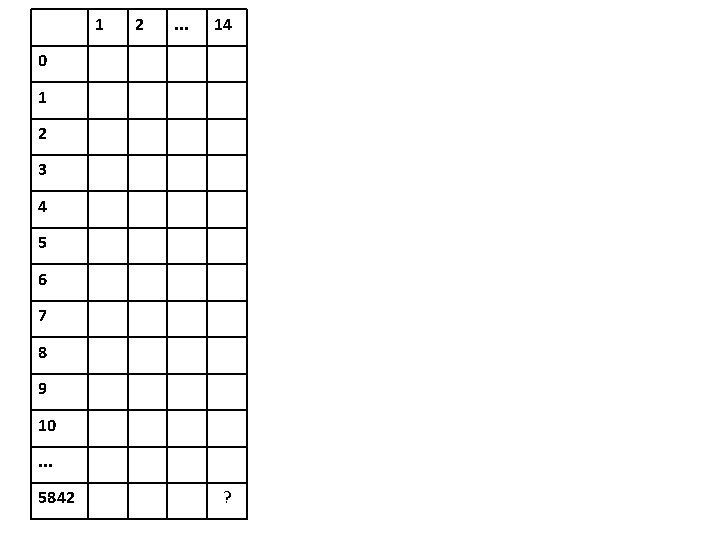
1 2 . . . 14 0 1 2 3 4 5 6 7 8 9 10. . . 5842 ?
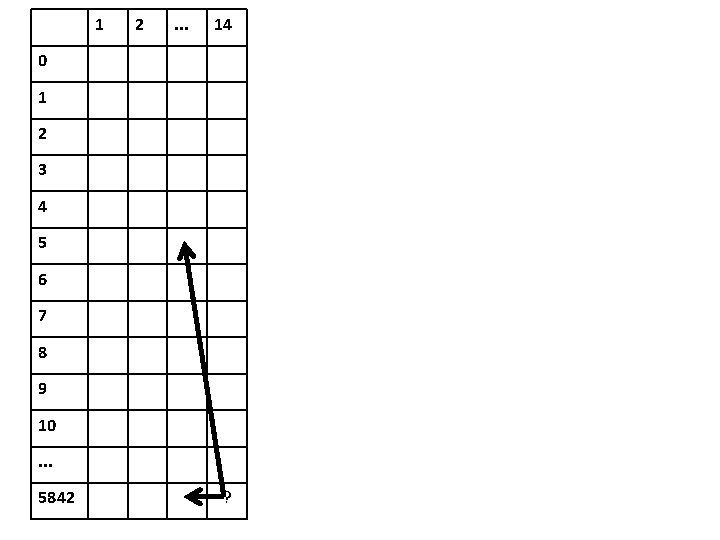
1 2 . . . 14 0 1 2 3 4 5 6 7 8 9 10. . . 5842 ?
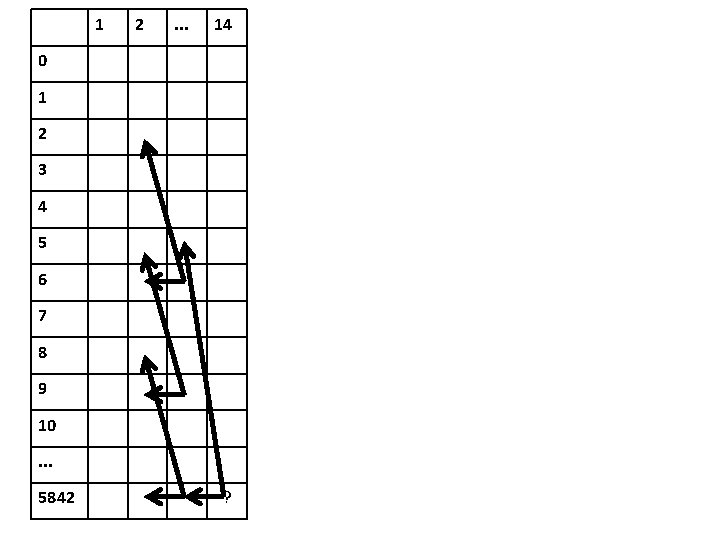
1 2 . . . 14 0 1 2 3 4 5 6 7 8 9 10. . . 5842 ?
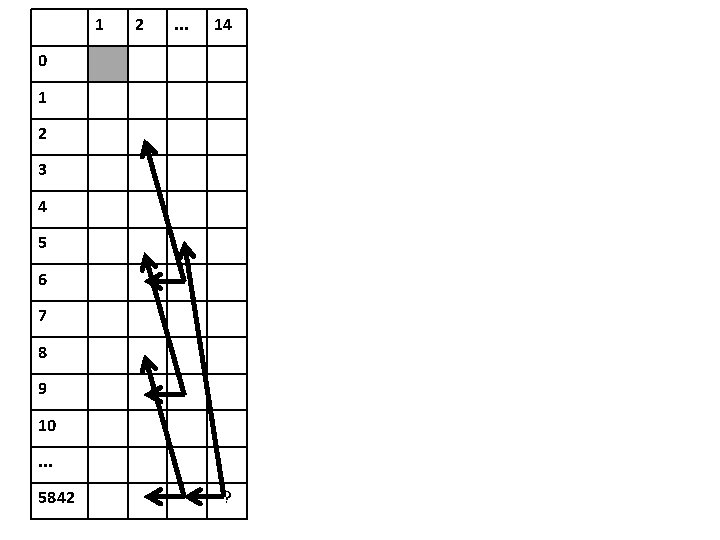
1 2 . . . 14 0 1 2 3 4 5 6 7 8 9 10. . . 5842 ?
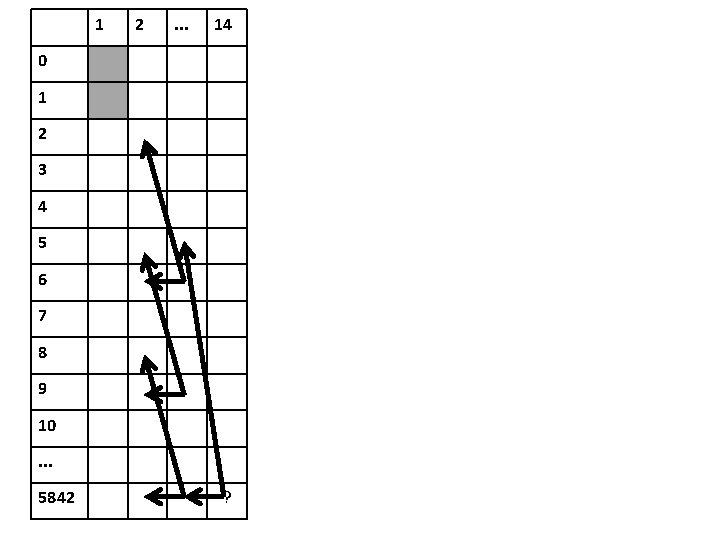
1 2 . . . 14 0 1 2 3 4 5 6 7 8 9 10. . . 5842 ?
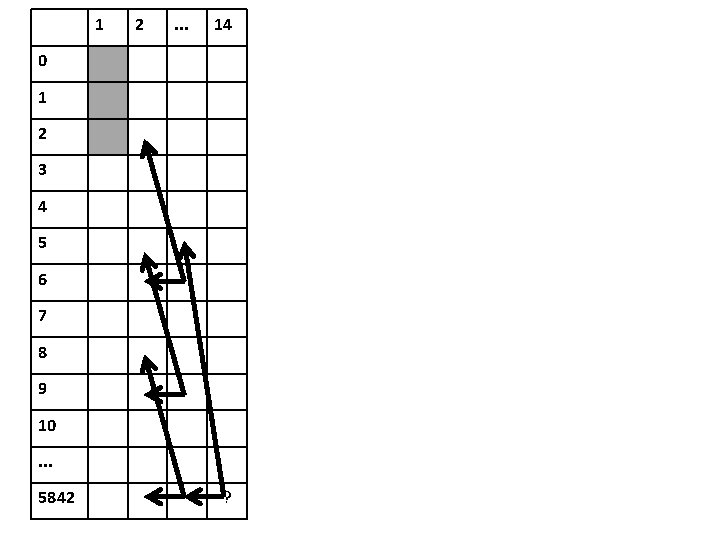
1 2 . . . 14 0 1 2 3 4 5 6 7 8 9 10. . . 5842 ?
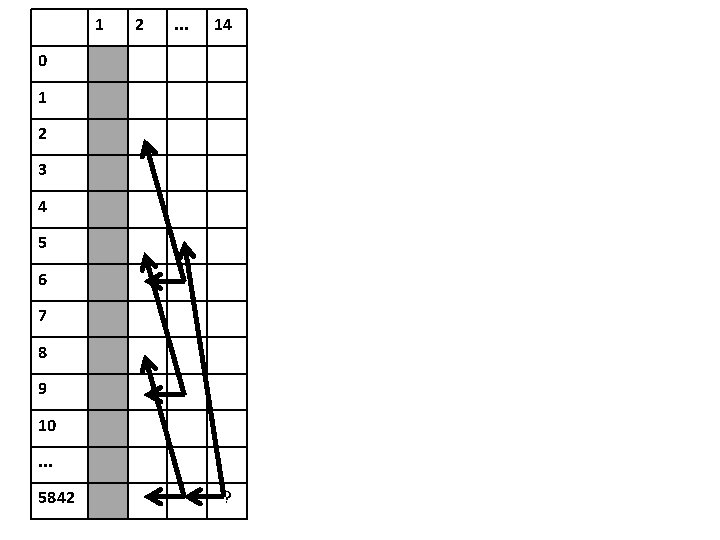
1 2 . . . 14 0 1 2 3 4 5 6 7 8 9 10. . . 5842 ?
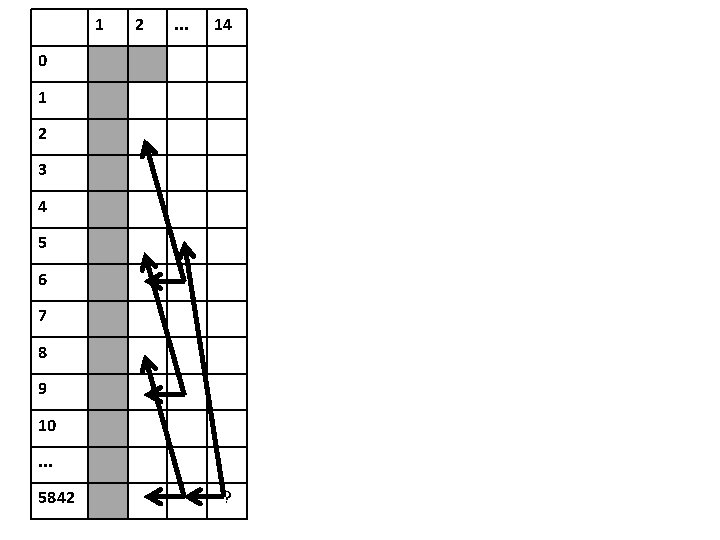
1 2 . . . 14 0 1 2 3 4 5 6 7 8 9 10. . . 5842 ?
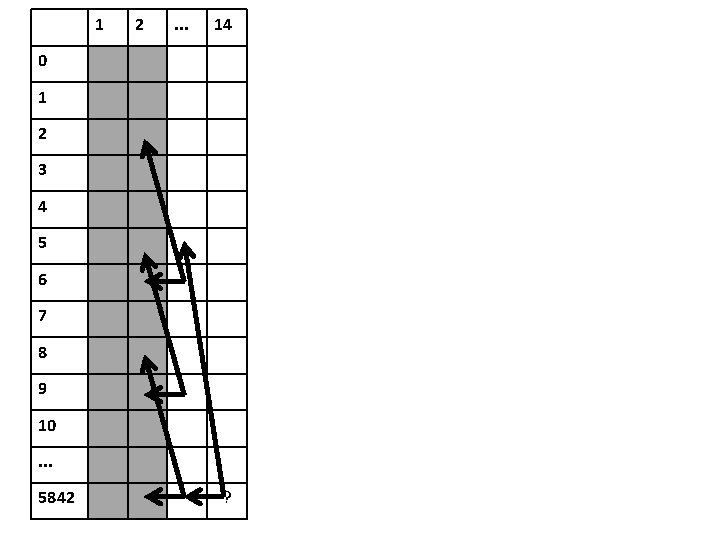
1 2 . . . 14 0 1 2 3 4 5 6 7 8 9 10. . . 5842 ?
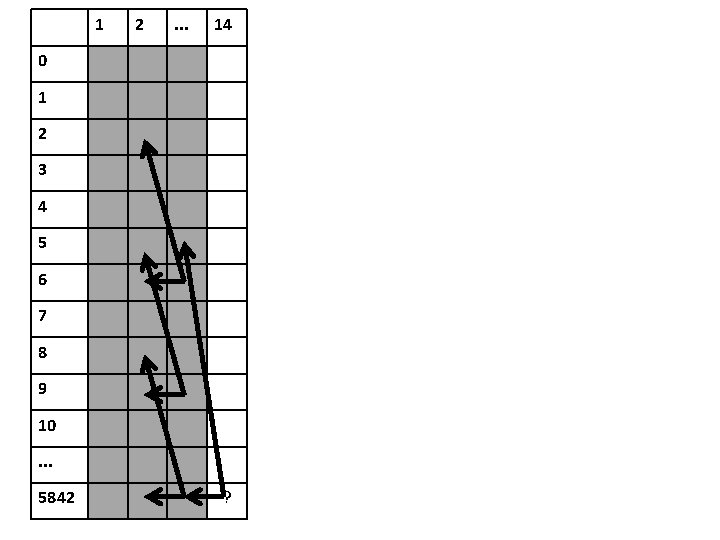
1 2 . . . 14 0 1 2 3 4 5 6 7 8 9 10. . . 5842 ?
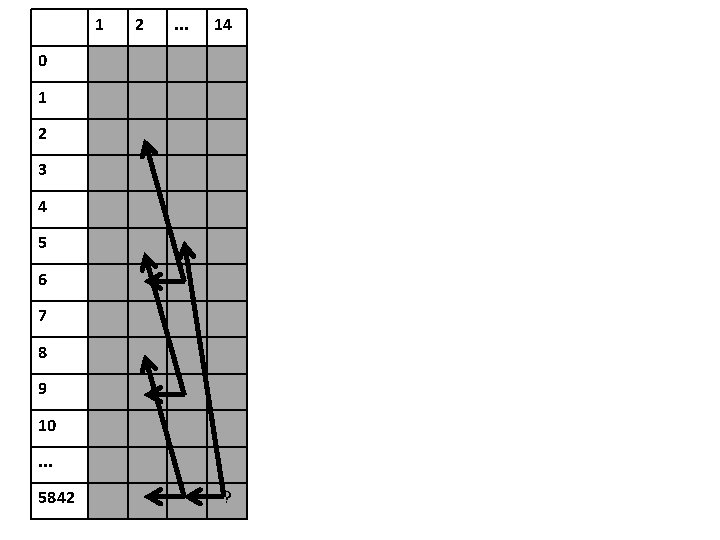
1 2 . . . 14 0 1 2 3 4 5 6 7 8 9 10. . . 5842 ?

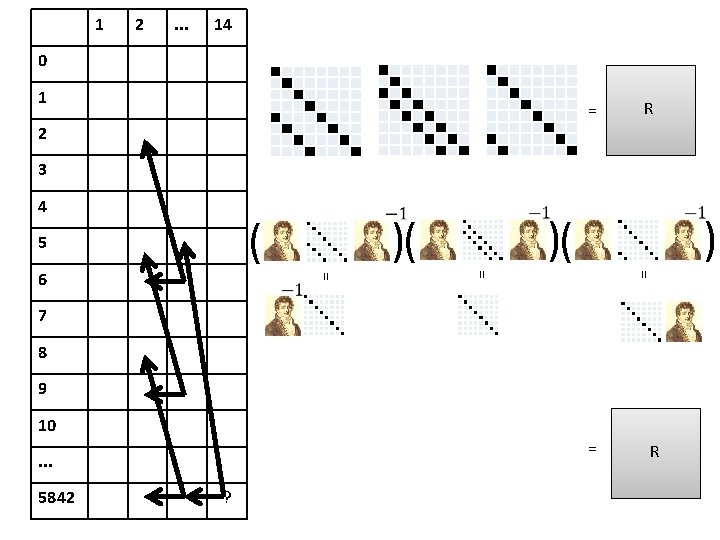
Subset Sum • = ( )
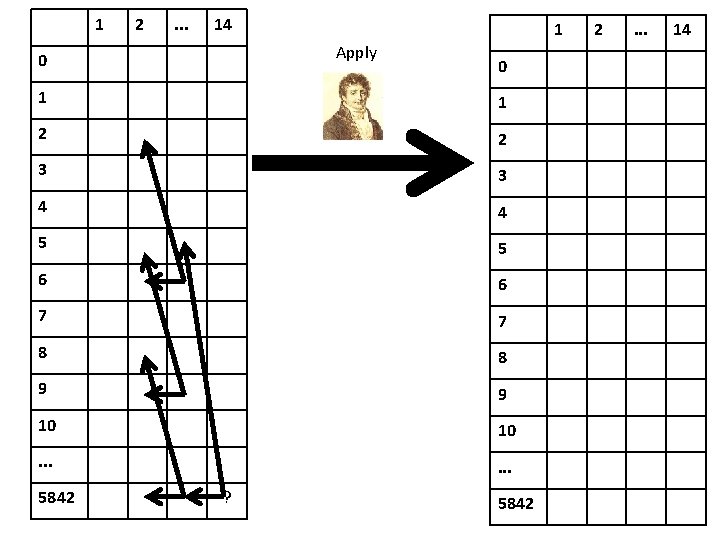
1 2 . . . 14 1 Apply 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 . . . 5842 ? 5842 2 . . . 14
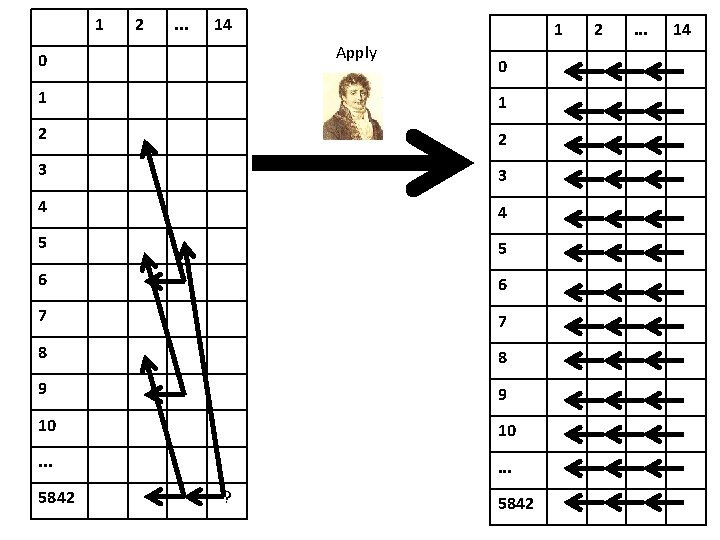
1 2 . . . 14 1 Apply 0 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 . . . 5842 ? 5842 2 . . . 14
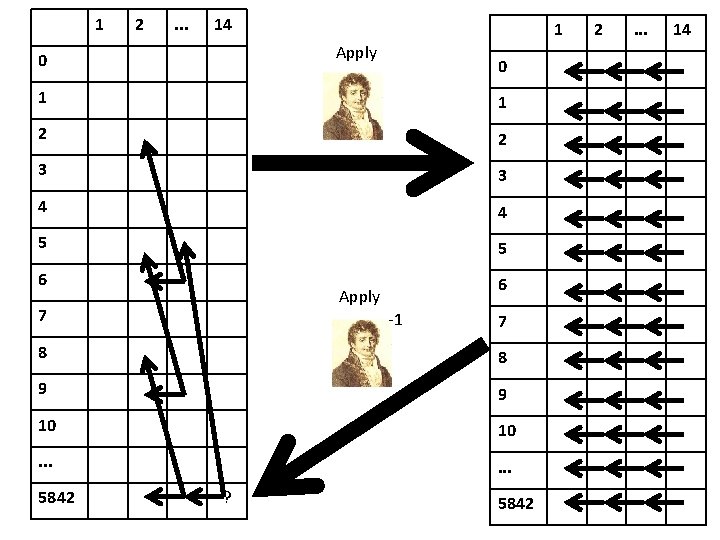
1 2 . . . 14 1 Apply 0 0 1 1 2 2 3 3 4 4 5 5 6 6 Apply 7 -1 7 8 8 9 9 10 10 . . . 5842 ? 5842 2 . . . 14
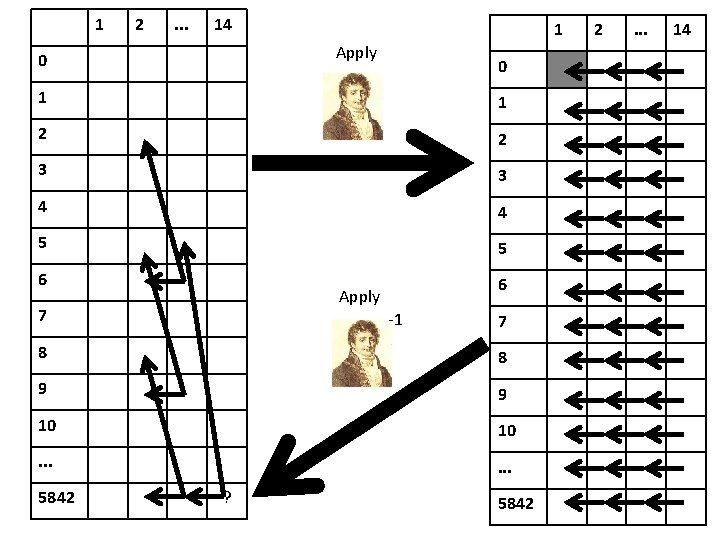
1 2 . . . 14 1 Apply 0 0 1 1 2 2 3 3 4 4 5 5 6 6 Apply 7 -1 7 8 8 9 9 10 10 . . . 5842 ? 5842 2 . . . 14
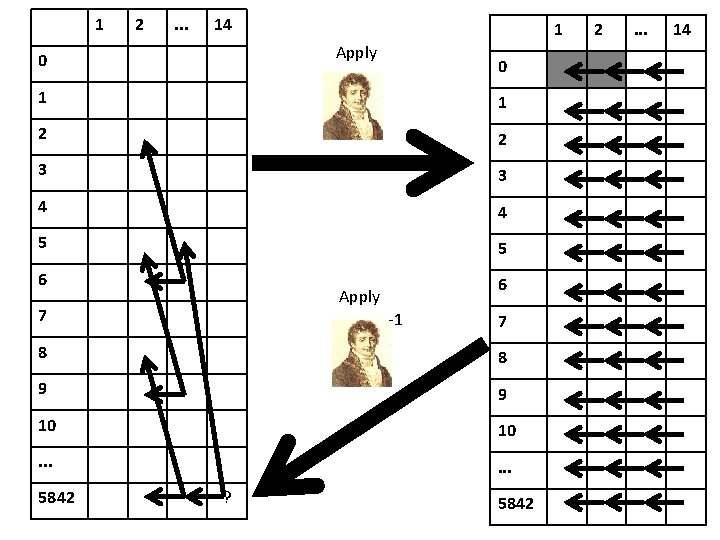
1 2 . . . 14 1 Apply 0 0 1 1 2 2 3 3 4 4 5 5 6 6 Apply 7 -1 7 8 8 9 9 10 10 . . . 5842 ? 5842 2 . . . 14
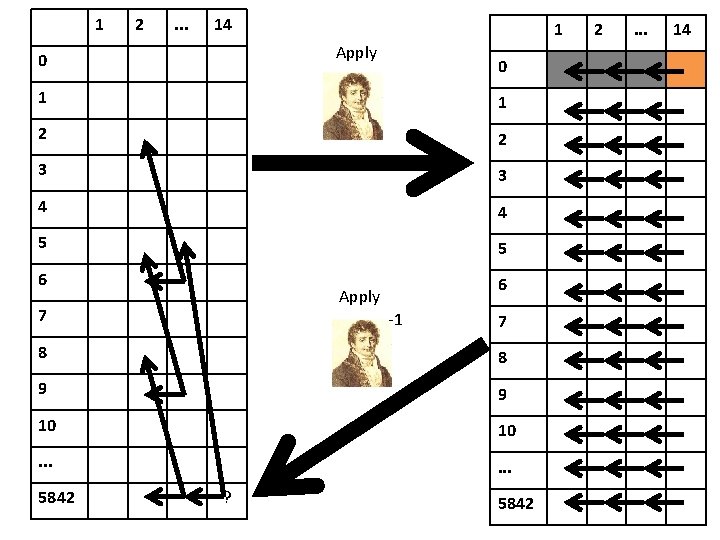
1 2 . . . 14 1 Apply 0 0 1 1 2 2 3 3 4 4 5 5 6 6 Apply 7 -1 7 8 8 9 9 10 10 . . . 5842 ? 5842 2 . . . 14
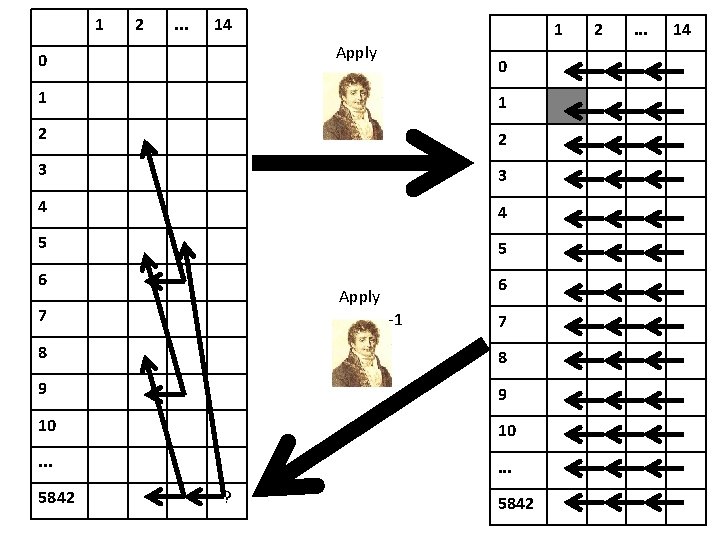
1 2 . . . 14 1 Apply 0 0 1 1 2 2 3 3 4 4 5 5 6 6 Apply 7 -1 7 8 8 9 9 10 10 . . . 5842 ? 5842 2 . . . 14
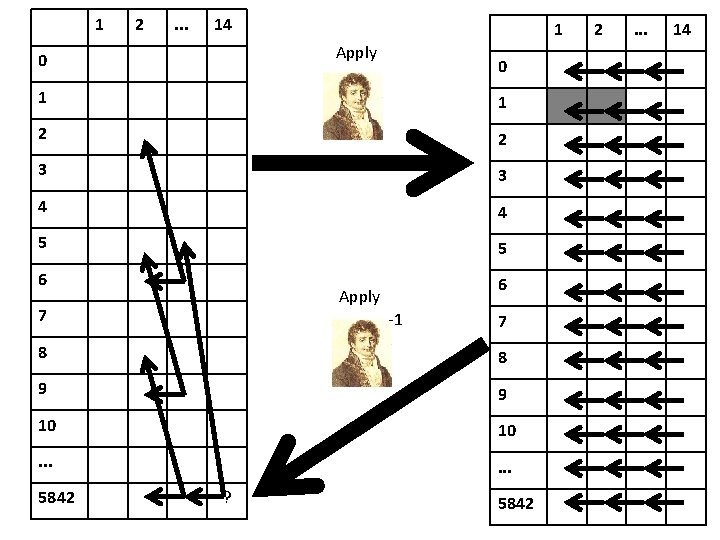
1 2 . . . 14 1 Apply 0 0 1 1 2 2 3 3 4 4 5 5 6 6 Apply 7 -1 7 8 8 9 9 10 10 . . . 5842 ? 5842 2 . . . 14
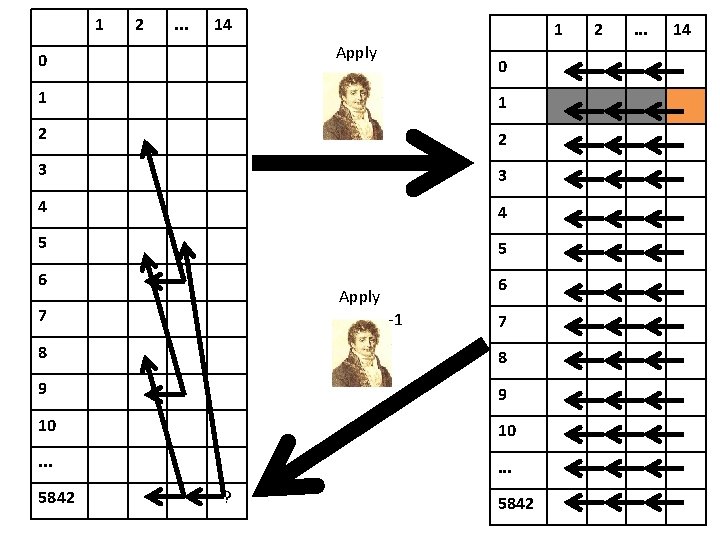
1 2 . . . 14 1 Apply 0 0 1 1 2 2 3 3 4 4 5 5 6 6 Apply 7 -1 7 8 8 9 9 10 10 . . . 5842 ? 5842 2 . . . 14
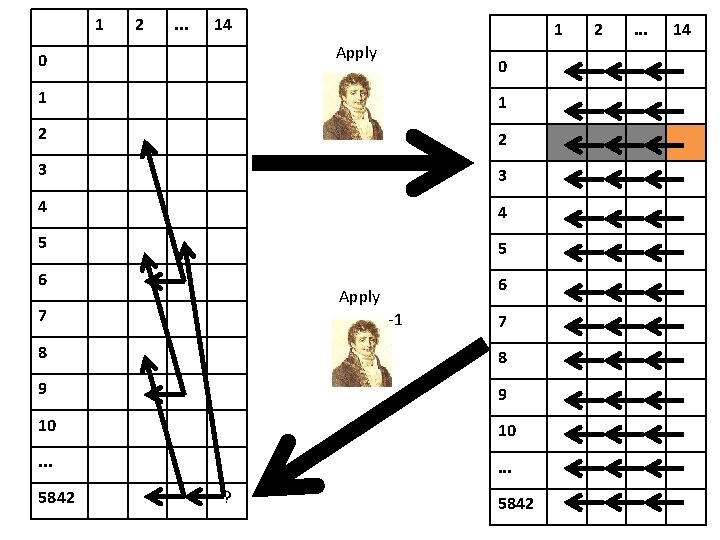
1 2 . . . 14 1 Apply 0 0 1 1 2 2 3 3 4 4 5 5 6 6 Apply 7 -1 7 8 8 9 9 10 10 . . . 5842 ? 5842 2 . . . 14
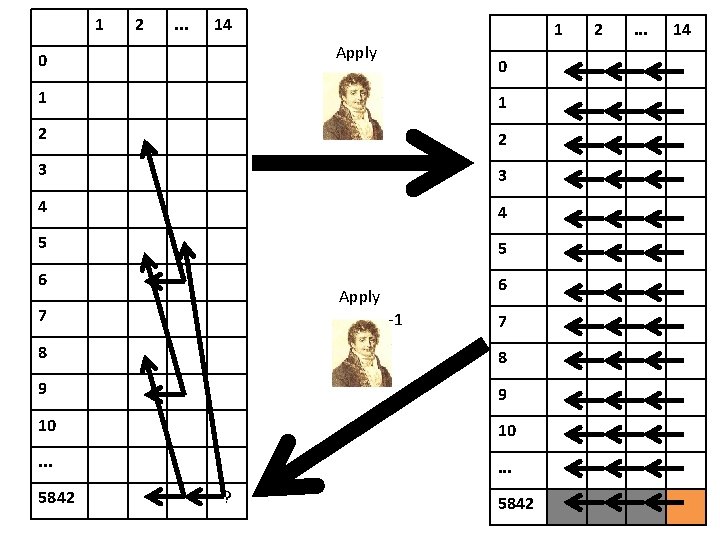
1 2 . . . 14 1 Apply 0 0 1 1 2 2 3 3 4 4 5 5 6 6 Apply 7 -1 7 8 8 9 9 10 10 . . . 5842 ? 5842 2 . . . 14

Fourier transform for Subset Sum • This works because of two reasons: – The fact that the transformation is invertible assures we can recover the required value from the transformed values. – The fact that the dependence in the transformed table becomes simpler assures we gain something by using the transformation. • In general, many tricks for multiplying chain of (explicit) matrices quickly – What if some of the matrices have low rank?

Subset Sum •

Fast Linear Algebra

Matrix Multiplication a b c d X e f g h = ae+bg af+bh ce+dg cf+dh • Seems to require 8 multiplications. • Multiplying nxn matrices seems to take n 3 multiplications. • Was thought by researchers for a while as well • But then…. in 1969…… : n 2. 81 multiplications! Volker Strassen

Matrix Multiplication a b c d X M 1: (a+d)(e+h) M 2: (c+d)e M 3: a(f-h) M 4: d(g-e) M 5: (a+b)*h M 6: (c-a)*(e+f) M 7: (b-d)*(g+h) e f g h = ae+bg af+bh ce+dg cf+dh = M 1+M 4 -M 5+M 7 M 3+M 5 M 2+M 4 M 1 -M 2+M 3+M 6
Matrix Multiplication X =
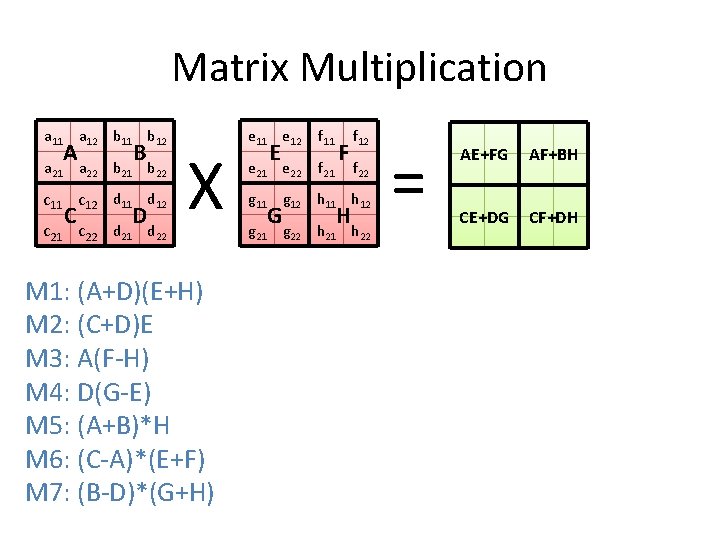
Matrix Multiplication a 11 a 21 A a 12 b 11 b 12 B a 22 b 21 b 22 c 11 c 12 d 11 d 12 C c 21 c 22 D d 21 d 22 X M 1: (A+D)(E+H) M 2: (C+D)E M 3: A(F-H) M 4: D(G-E) M 5: (A+B)*H M 6: (C-A)*(E+F) M 7: (B-D)*(G+H) e 11 e 12 f 11 e 22 f 21 E g 11 g 21 G F f 12 f 22 g 12 h 11 h 12 H g 22 h 21 h 22 = AE+FG AF+BH CE+DG CF+DH = M 1+M 4 -M 5+M 7 M 3+M 5 M 2+M 4 M 1 -M 2+M 3+M 6
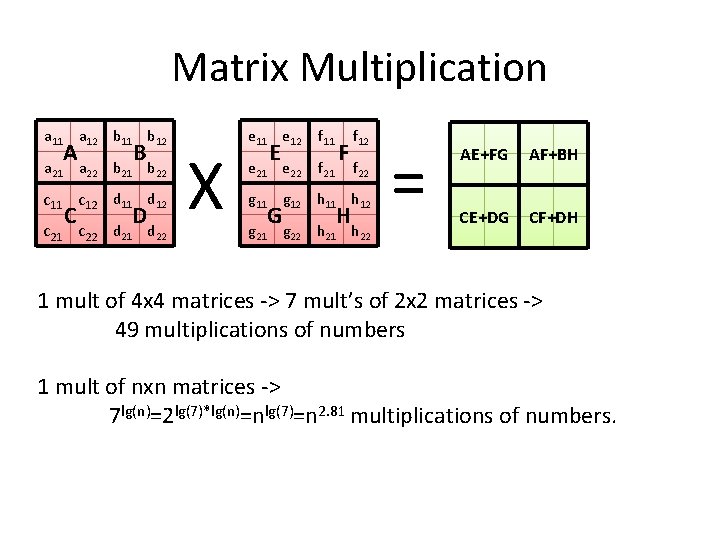
Matrix Multiplication a 11 a 21 A a 12 b 11 b 12 B a 22 b 21 b 22 c 11 c 12 d 11 d 12 C c 21 c 22 D d 21 d 22 X e 11 e 12 f 11 e 22 f 21 E g 11 g 21 G F f 12 f 22 g 12 h 11 h 12 H g 22 h 21 h 22 = AE+FG AF+BH CE+DG CF+DH 1 mult of 4 x 4 matrices -> 7 mult’s of 2 x 2 matrices -> 49 multiplications of numbers 1 mult of nxn matrices -> 7 lg(n)=2 lg(7)*lg(n)=nlg(7)=n 2. 81 multiplications of numbers.
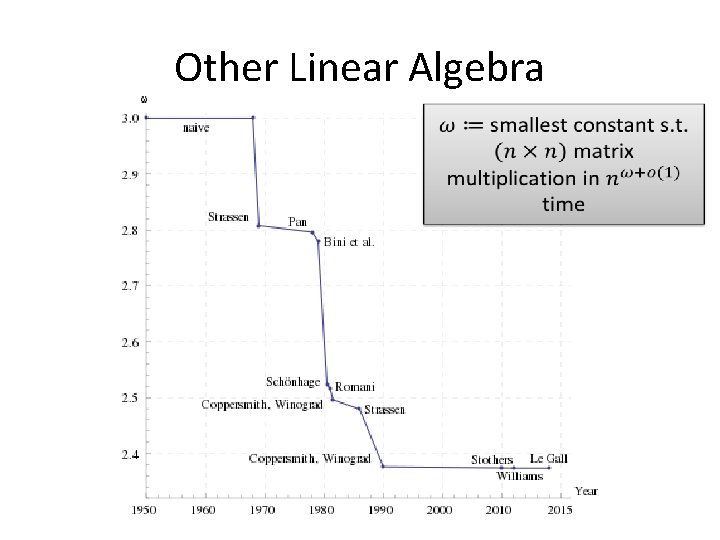
Other Linear Algebra

Group-Theoretic Matrix Mult • Natural idea, reduce to some polynomial multiplication • Cohn, Umans (and others): – Rephrases existing algorithms as embedding matrix mult in general polynomial multiplication (group algebra’s)

* This exposition is heavily based on a blog post (see notes) Other Linear Algebra • =

* This exposition is heavily based on a blog post (see notes) Other Linear Algebra • = X = I I
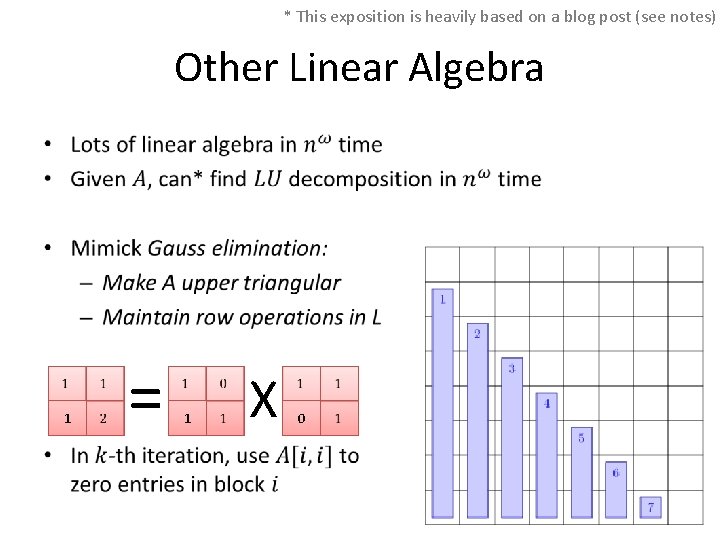
* This exposition is heavily based on a blog post (see notes) Other Linear Algebra • 1 = 1 X 0

* This exposition is heavily based on a blog post (see notes) Other Linear Algebra • 1 = 1 X 0

* This exposition is heavily based on a blog post (see notes) Other Linear Algebra •

* This exposition is heavily based on a blog post (see notes) Other Linear Algebra •

* This exposition is heavily based on a blog post (see notes) Other Linear Algebra •

* This exposition is heavily based on a blog post (see notes) Other Linear Algebra •

* This exposition is heavily based on a blog post (see notes) Other Linear Algebra •

* This exposition is heavily based on a blog post (see notes) Other Linear Algebra • Natural question: can we do some tasks faster? • No for matrix inversion:

Other Linear Algebra • * * x 1 * + x 2 x 3 … xn

Other Linear Algebra •

Other Linear Algebra •

Freivalds’ Algorithm (1977) ● Freivalds’ variant of problem: Determine whether n n matrices A, B, and C satisfy the condition AB = C ● Method: – – Choose x {0, 1}n randomly and uniformly (vector of length n) If ABx ≠ Cx then report “AB ≠ C” else report “AB = C probably”

Running Time ● ● ● ABx = A(Bx), so we have 3 instances of an n n matrix times an n-vector These are O(n 2) time operations if done straightforwardly Total running time O(n 2)

How Often Is It Wrong? •

Decreasing the Probability of Error ● By iterating with k random, independent choices of x, we can decrease probability of error to 1/2 k, using time O(kn 2)

Yates’ Algorithm •
- Slides: 80