Algebraic Expressions with a Technical Example Evaluating Algebraic

Algebraic Expressions with a Technical Example Evaluating Algebraic Expressions Evaluating Expressions Using Technical Applications 1

Algebraic Expressions with a Technical Example Technical Application Scientists, engineers and technicians need, develop, and use mathematics to explain, describe, and predict what nature, processes, and equipment do. Many times the math they use is the math that is taught in ALGEBRA 1! 2

Algebraic Expressions with a Technical Example There are 3 Objectives of this presentation: 1) To evaluate algebraic expressions involving multiplication and division of real numbers. 2) To simplify algebraic expressions by using the rules for order operations to evaluate algebraic expressions. 3) To use algebra 1 to help understand a technical application. 3

Algebraic Expressions with a Technical Example Evaluating Expressions The rules for dividing real numbers involves the mathematical concept of RECIPROCALS. The division by a number is defined as multiplying by the reciprocal or multiplicative inverse of the number. TWO EXAMPLES A common symbol technicians, scientists and engineers use for multiplication. (a) Specific Situation -27 3 = (-27) The fraction one third is the reciprocal of 3 1 ( 3 ) = -27 3 = -9 Divide – 27 by 3 is the same as multiply – 27 by the reciprocal of 3. the fraction ( (b) General Situation ( 1 d) 2 1 ) b is the reciprocal of b b = ( 1 d) ( 1 ) 2 b 1 ) ( d ) ( 1 )= ( d ) =( 2 1 b 2 b 4

Algebraic Expressions with a Technical Example Evaluating Expressions The division by a number is defined as multiplying by the reciprocal or multiplicative inverse of the number. 4 EASY PRACTICE PROBLEMS (a) Divide the number 1 by the number 4 11 = 11? 4 The fraction one fourth 1 = 0. 25 4 is the reciprocal of the number 4 Dividing 1 by 4 is the same as multiplying 1 by the fraction 1 4 Dividing 1 by 4 is the same as multiplying 1 by the reciprocal of the number 4 1 is the reciprocal of the number 4 4 5

Algebraic Expressions with a Technical Example Evaluating Expressions The division by a number is defined as multiplying by the reciprocal or multiplicative inverse of the number. 4 EASY PRACTICE PROBLEMS (continued) (b) 1 = 1? 9 1 = 0. 11 9 6

Algebraic Expressions with a Technical Example Evaluating Expressions The division by a number is defined as multiplying by the reciprocal or multiplicative inverse of the number. 4 EASY PRACTICE PROBLEMS (continued) (c) If the values of d and b are 5 and 36 respectively, what is the value of the following algebraic expression? ( 1 ) (d ) 10 1 1 b = (? 10 d ) ( b ) = ( 1 5 ) ( 1 ) = 10 36 The variable b and the variable are reciprocals of each other. 1 5 = ( 10 ) ( 36 ) 1 b = (0. 10) (0. 14) = 0. 014 7

Algebraic Expressions with a Technical Example Evaluating Expressions The division by a number is defined as multiplying by the reciprocal or multiplicative inverse of the number. 4 EASY PRACTICE PROBLEMS (continued) (d) Sometimes it is fun in Algebra to use a letter from the Greek alphabet as well as letters like “d” and “b”. Try the following problem using the Greek letter LAMBDA l l= d l= ? 1 ( 10 b the Greek letter Lambda ) when b equals 36 and d equals 5. 8

Algebraic Expressions with a Technical Example Evaluating Expressions The rules for dividing real numbers involve the mathematical concept of reciprocals. The division by a number is defined as 1 What is the by reciprocal of ? multiplying the reciprocal or multiplicative inverse of the number. ( 10 b ) 4 Easy Practice Problems (continued) (d) l= d l= ? d 1 ( 10 b l ) when b equals 36 and d equals 5. 1 ( 10 b ) ( 10 b ) = ? (d ) 1 l = (5 10 36) l = (5 360 ) l = 1800 9 the Greek letter Lambda

Algebraic Expressions with a Technical Example Evaluating Expressions Technicians, scientists and engineers use Algebra all the time. When using algebra, they also like to use combinations of letters and numbers as algebra symbols. The previous example problem used the Greek letter lambda as well as the letters “d” and “b”. l= d 1 ( 10 b ) A technician might use this algebraic expression with lambda and the letters “d” and “b” replaced by symbols that are combinations of letters and numbers. l 1 = d 1 10 ( 1 10 b 1 )

Algebraic Expressions with a Technical Example Evaluating Expressions What is the reciprocal of ( 10 d 1 ) ? Technicians, scientists and engineers use Algebra all the time. However, they also like to use combinations of letters and numbers as algebra symbols. l 1 = d 1 l 1 = (d ? 1 ) 1 ( ) 10 b 1 when b 1 equals 36 and d 1 equals 5. ( 10 b 1 ) = ( 5 10 36) = 1800 1 PRACTICE PROBLEM when b 1 equals 36 and d 1 equals 5. l 2 = b 1 1 ( 10 d 1 ) = ? b 1 ( ) 10 d 1 1 36 2 = 36 ( 10 5 ) = 50 = 0. 72 l 11

Algebraic Expressions with a Technical Example Scientists, technicians and engineers also use algebraic symbols that are combinations of letters and numbers because they often work with the same algebraic expression substitute different numbers. but substitute TWO QUICK EXAMPLE PROBLEMS These examples use the following algebraic expression; l (1) = d 1 ( 1 10 b 1 ) Let b 1 equal 36 and d 1 equal 5. l 1 = (d ? 1 ) ( 10 b 1 ) = ( 5 10 36) = 1800 1 (2) This time, let b 1 equal 35 and d 1 equal 5. l 2 10 b )= ( 5 10 35) = 1750 ) =( d ? ( 1 12

Algebraic Expressions with a Technical Example Sometimes an engineer, scientist or technician may select symbols that are similar when the algebraic expressions are different. This often happens when there is a connection between the answers after the expressions have been evaluated. 2 EASY EXAMPLE PROBLEMS (1) (2) In both problems b 1 equals 35 and d 1 equals 5. l 1= (10 d 1 ) l 2= b 1 = (? 50) ( (10 d 1 ) = (? 35) ( 13 1 10 ) = ( ) = 1. 43 35 7 7 1 ) = ( ) = 0. 7 50 10

Algebraic Expressions with a Technical Example Evaluating Expressions (1) l 1= (10 d 1 ) b 1 = (? 50) (2) l 2= b 1 (10 d 1 ) = (? 35) ( ( 1 )= ( 10 ) = 1. 43 35 7 1 7 ) = ( ) = 0. 7 50 10 What is the connection between l 1 and l 2 ? l 1 is the reciprocal of l 2 Or, if you wish l is the reciprocal of l ? 2 1 ( l 1) ( l 2 ) = (1. 43) (0. 7) = 1. 00 1 14

Algebraic Expressions with a Technical Example THREE QUICK REVIEW QUESTIONS to see what we remember If l 1 = 1. 43 and 1) What is the connection between l =2 0. 7 l 1 and l 2 ? One is the reciprocal of the other. 2) What is the answer if you multiply reciprocals together? You always get the number 1 as the answer. Try this with a calculator. 3) What is the reciprocal of ( 10 d 1 ) ? 1 ( ) 10 d 1 15 Is there a problem?

Algebraic Expressions with a Technical Example What do you think? 1) Is one half the reciprocal of 2? Why/why not? 2) Do all fractions have reciprocals? Why/Why not? 3) Two of the most popular manufacturers of calculators (TI and HP) have a different style (way to do calculation) for getting answers to multiplication and division problems. One of them was developed with a knowledge (use) of reciprocals in mind. Which one is it? Why? 4) Use the Web (if you have to) and examine the arrangement of the scales on a slide rule. One of those scales is know as the reciprocal scale. Which one is it and why is it named so? 16

Algebraic Expressions with a Technical Example 2) Simplifying Expressions Evaluating Expressions Objective: To simplify algebraic expressions by using the rules for order operations to evaluate algebraic expressions 17

Algebraic Expressions with a Technical Example Simplifying Expressions Rules Perform operations within parentheses first. Multiply (divide) in order from left to right. Add (subtract) in order from left to right. TWO EXAMPLES (a) 14 - 10 3 +10 = 14 -30+10 =-16 +10= -4 (b) ( 1 10 4 9 ) ( ) = 1 0. 25 - 0. 11 10 1 = 10 ( 0. 14 ) 18 ( 0. 14)= = 0. 1 0. 014

Algebraic Expressions with a Technical Example Simplifying Expressions Rules that help the Simplification of Expressions Perform operations within parentheses parenthesis first. Multiply (divide) in order from left to right. Add (subtract) in order from left to right. TWO SIMPLE EXAMPLES (a) 14 - (10 3) +10 = ? = 14 - (10 3) +10 = = 14 -30+10 = = -16 +10= -4 19

Algebraic Expressions with a Technical Example Simplifying Expressions 1 1 (b) ( ) = 10 ( 0. 25 - 0. 11 ) 10 4 9 1 0. 014 = ( 0. 14 ) = 0. 1 (0. 14 ) = 0. 014 10 Rules used? Perform operations within parentheses first. Multiply (divide) in order from left to right. Another way that technicians, scientists and engineers often simplify this type of algebraic expression. ( 1 10 4 9 ) (9 -4) 1 = 10 (4 9) ( ) Rule to use first? Perform operations within parenthesis. 20 ( ) 5 = 1 10 36 1 0. 014 = 10 0. 14 = 0. 014 =

Algebraic Expressions with a Technical Example Simplifying Expressions Rules that help the Simplification of Expressions Perform operations within parentheses first. Multiply (divide) in order from left to right. Add (subtract) in order from left to right. TWO GENERALIZED EXAMPLES (a) 1 10 ( 1 - 1 b d ) 1 = 10 For the previous problem, b was equal to 4 and d was equal to 9 (d – b) (b d) ( ) 1 10 4 9 21

Algebraic Expressions with a Technical Example Simplifying Expressions 1 10 (1 - 1) = b 1 10 d (d – b) (b d) ( ) Technical workers often use different symbol combinations for the letters b and d. (b) 1 1 1 - 1 = 10 n 1 n 2 10 ( ) ( (n 2– n 1) (n 1 n 2) ) This time, the symbol n 1 replaces the letter b, and the symbol n 2 replaces the letter d. 22

Algebraic Expressions with a Technical Example Simplifying Expressions Simplification of a new expression: ( ) =? 1 1 1 - 2 2 10 n 1 n 2 This time, let n 1 equal 2 and n 2 equal 3 1 1 - 1 1 = 10 2 2 3 2 10 ( ) (9 -4) ( (4 = ? 1 10 ) 9) ( ) 5 36 ( Note: The calculations inside the parentheses were completed before multiplying by one tenth. 23 ) = 1 0. 14 = 0. 014 10

Algebraic Expressions with a Technical Example Simplifying Expressions Reciprocal Expressions Rules Perform operations within parenthesis parenthesesfirst. Multiply (divide) in order from left to right. Add (subtract) in order from left to right. THREE EASY EXAMPLE PROBLEMS a) 1 [10] b) 1 -1 = [ 10] = 0. 10 There is nothing to do inside this parenthesis. = 1 [2 + 3(2) +2] [2 + 6 +2] [10] -1 = [10] = 0. 10 There is something to do inside this parenthesis. 24

Algebraic Expressions with a Technical Example Simplifying Expressions Reciprocal Expressions Rules Perform operations within parentheses first. c) 1 [ ( 20 3 1 4 4 )] = 1 1 [ ( )] 20 2 4 -1 [ ] = This version is=popular 10 in technical applications because 10 up less space on a it takes [ ] piece of paper and is easier to type on a computer. A typical reciprocal (inverse) expression used in technology. 1 [ (n 1 10 1 2 1 - 1 )] n 22 = [ ( -1 )] 1 1 1 - 2 2 10 n 1 n 2 These two expressions are same. 25

Algebraic Expressions with a Technical Example Simplifying Expressions Reciprocal Expressions Rules Perform operations within parentheses first. PRACTICE PROBLEM 1 [ (n 1 10 1 2 1 - 1 )] = [ ( 1 10 n 22 -1 )] 1 1 - 2 2 n 1 n 2 What is the value of this expression when n 1 equals 2 and n 2 equals 3? 26

Algebraic Expressions with a Technical Example Simplifying Expressions Note: Perform operations within parenthesis first 0. 014 ] [ 1 1 1 [ 10 (n -(n )]) 1) 2) -1 2 1 -1 ( = 1 0. 014 ) Note: 2 = 2 times 2 = 4 2 is the number 71. 4 2 3 = 3 times 3 = 9 21 2 0. 014 n 1 equals 2 and n 2 equals 3 [ )] 1 1 - 1 2 2 10 2 3 ( -1 -1 [ ( (4 9) )] 5 1 1 0. 14 = = [ 10( 36) ] [ 10 ( )] = [ 0. 014 ] = 71. 4 = (9 -4) 1 10 -1 -1 27 -1 The calculation of the inverse is the last thing done

Algebraic Expressions with a Technical Example Simplifying Expressions THREE QUICK REVIEW QUESTIONS. 1) What are, in the correct order of use, the rules for simplifying algebraic expressions? Perform operations within parentheses first. Multiply (divide) in order from left to right. Add (subtract) in order from left to right. 2) What is another way to write the following algebraic expression? ( 1 - 1 n 2 ) ( = 3) What is (a) the inverse of ( (n 2– n 1) (n 1 n 2) 1 0. 014 )? ) 71. 4 (b) the reciprocal of the number 71. 4? 28 ( 1 0. 014 )

Algebraic Expressions with a Technical Example Simplifying Expressions What do you think? 1) Are the two algebraic expressions show below equal? Why/why not? (a) 1 [ (n 1 10 2) (b) 1 2 1 - 1 )] 2 n 22 [ ( 1 10 )] 1 1 - 2 2 n 1 n 2 Is the inverse of a number always the same as the reciprocal of that number? Why/Why not? 29 -2

Algebraic Expressions with a Technical Example 3) Technology Application Simplifying Expressions Objective: To use algebraic expressions to describe and understand a technical application. 30
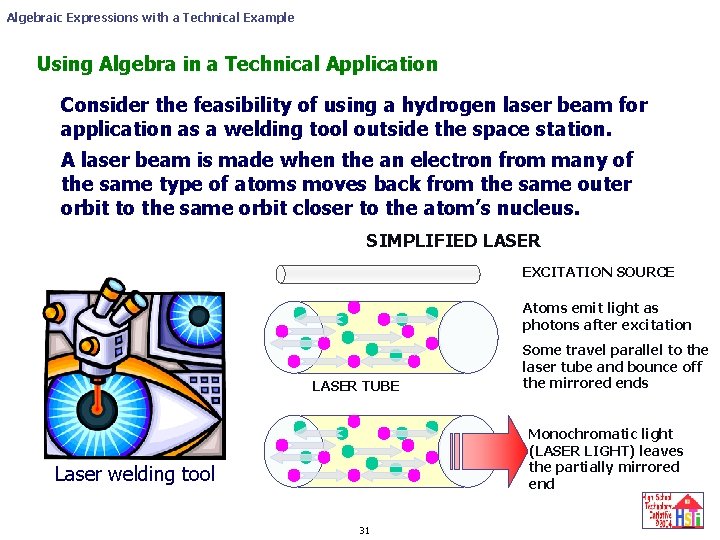
Algebraic Expressions with a Technical Example Using Algebra in a Technical Application Consider the feasibility of using a hydrogen laser beam for application as a welding tool outside the space station. A laser beam is made when the an electron from many of the same type of atoms moves back from the same outer orbit to the same orbit closer to the atom’s nucleus. SIMPLIFIED LASER EXCITATION SOURCE Atoms emit light as photons after excitation LASER TUBE Some travel parallel to the laser tube and bounce off the mirrored ends Monochromatic light (LASER LIGHT) leaves the partially mirrored end Laser welding tool 31
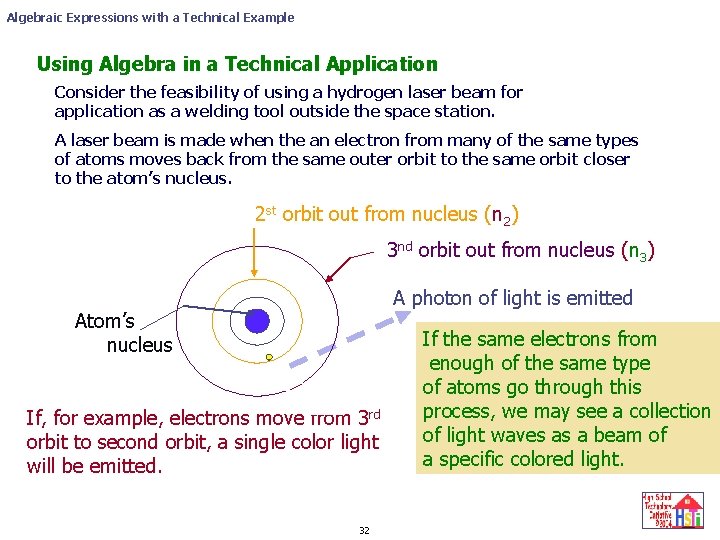
Algebraic Expressions with a Technical Example Using Algebra in a Technical Application Consider the feasibility of using a hydrogen laser beam for application as a welding tool outside the space station. A laser beam is made when the an electron from many of the same types of atoms moves back from the same outer orbit to the same orbit closer to the atom’s nucleus. 2 st orbit out from nucleus (n 2) 3 nd orbit out from nucleus (n 3) A photon of light is emitted Atom’s nucleus If, for example, electrons move from 3 rd orbit to second orbit, a single color light will be emitted. 32 If the same electrons from enough of the same type of atoms go through this process, we may see a collection of light waves as a beam of a specific colored light.
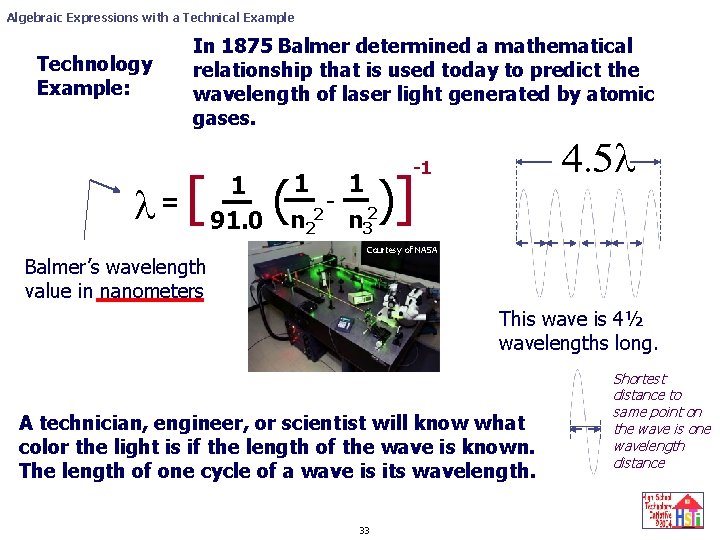
Algebraic Expressions with a Technical Example Technology Example: In 1875 Balmer determined a mathematical relationship that is used today to predict the wavelength of laser light generated by atomic gases. l= [ Balmer’s wavelength value in nanometers 1 91. 0 ( 4. 5 l -1 )] 1 1 - 2 2 n 3 Courtesy of NASA This wave is 4½ wavelengths long. A technician, engineer, or scientist will know what color the light is if the length of the wave is known. The length of one cycle of a wave is its wavelength. 33 Shortest distance to same point on the wave is one wavelength distance

Algebraic Expressions with a Technical Example If the light beam for a hydrogen gas laser is to be generated when one electron from many individual hydrogen atoms in the gas move from the 3 rd orbit to the 2 nd orbit, what color is the light that is observed. Technology Application Problem Statement l [ ( = 1 91 Symbol people use to represent the wavelength value in nanometers -1 )] 1 1 - 1 2 2 2 3 91 )] =[ ( 1 1 - 2 2 n 3 l -1 -1 [ ( (4 9) )] (9 -4) =? 1 91 -1 -1 [ ( ) ] [ ( )] 0. 0015] = 670 nanometers [ = l l = 5 1 91 36 34 = -1 1 0. 14 91

Algebraic Expressions with a Technical Example Technology Application Problem Statement If the light beam for a hydrogen gas laser is to be generated when an electron moves from the 3 rd orbit to the 2 nd orbit of many individual hydrogen atoms in the gas, what color is the light that is observed? l = [ 1 91 ( 1 n 1 2 - wavelength value -1 l = [0. 0015 ] 1 2) n 2 -1 ] 1 5 -1 ( ) = [ 91 36 ] 1 -1 = [ (0. 14 ) ] 91 = 670 nanometers The hydrogen laser will emit light of 670 nanometers What color do you thing the light wave is? 35

Algebraic Expressions with a Technical Example Technology Application Problem Statement If the light beam for a hydrogen gas laser is to be generated when an electron moves from the 3 rd orbit to the 2 nd orbit of many individual hydrogen atoms in the gas, what color is the light that is observed? The hydrogen laser will emit light of 670 nanometers 657 nm 486 nm 434 nm 410 nm What color do you thing the light wave is? The 670 nm light emitted from the hydrogen laser will be slightly to the right of the color at 657 nm 36

Algebraic Expressions with a Technical Example Technology Example: THREE QUICK REVIEW QUESTIONS l =2 670 What is the relationship between l and l ? 1 2 If 1) l 1 =. 0015 and They are complements. 2) What is the answer if you multiply complements together? You always get the number 1 Try this with a calculator. as the answer. What’s the problem? 3) What was the last name of the person who determined the mathematical model that is used to predict the color of light caused by electrons moving from one orbit to another? His last name was Balmer and he worked out his formula in 1875. 37

Algebraic Expressions with a Technical Example Technology Example: What do you think? 1) Do you think Balmer figured out his mathematical relationship so that he could understand the Bohr atomic model? Why/Why not? 2) Can you make a laser beam by focusing sun light through a prism? Why/ Why not? 3) Does the Balmer model predict that a laser beam will occur if electrons go from the 2 nd orbital to the first orbital of an atom? Why/why not. 38

Algebraic Expressions with a Technical Example 39
- Slides: 39