Algebraic Expressions Definition It is formed by combining

Algebraic Expressions

Definition: It is formed by combining numbers and variables using any of the four fundamental operations (+, -, x, ÷), powers and roots. • Examples: 2 x + 1 3 + 2 x 2 – y

Variables � are letters used to represent certain values or quantities. Example: 3 x + 2 variable

Vocabularies: o Term o Constants or constant terms o Variable Terms o Numerical Coefficients o Literal Coefficients

Term � numbers and letters combined by multiplication that serves as its major operation. Example: 2 x 3 y 2 (x + y)2 = (x + y)

Constants or Constant terms � are the terms that have no variables, only numbers. Variable Terms � terms that are not constants Example: 3 x 2 + 2 xy – 7 y 3 + 35 35 constant term variable terms 3 x 2, 2 xy, -7 y 3 (Note: algebraic expression does not contain the “=“ sign)

Numerical Coefficients � the number parts of each terms Literal Coefficients � literal number parts of each terms Example: 4 y 3 + 2 x 2 - 1 4, 2, -1 y 3, x 2 numerical coefficients literal coefficients

� The number of terms of an algebraic expression is determined by the plus and minus operations.

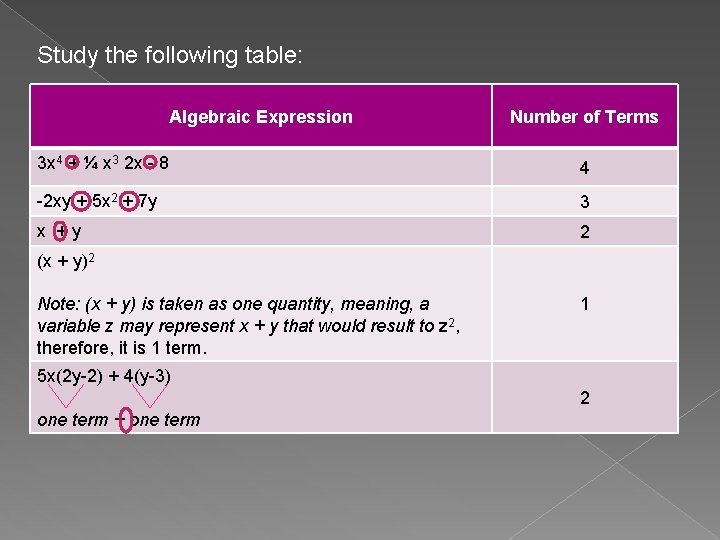
Study the following table: Algebraic Expression Number of Terms 3 x 4 + ¼ x 3 2 x - 8 4 -2 xy + 5 x 2 + 7 y 3 x +y 2 (x + y)2 Note: (x + y) is taken as one quantity, meaning, a variable z may represent x + y that would result to z 2, therefore, it is 1 term. 1 5 x(2 y-2) + 4(y-3) 2 one term + one term

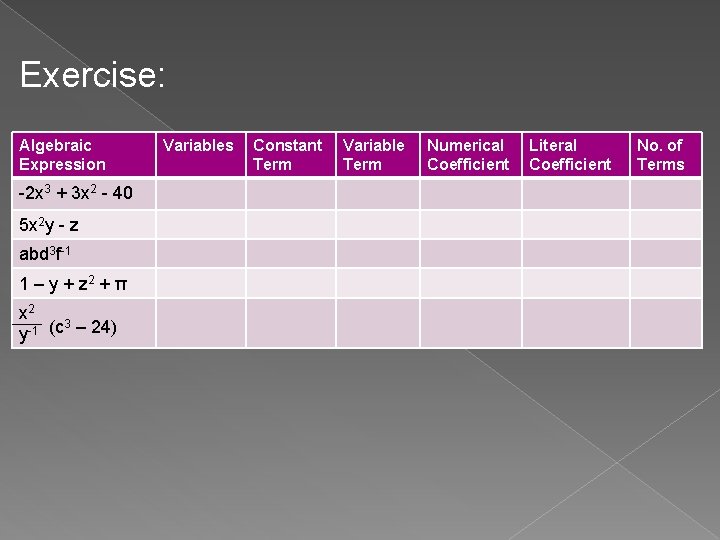
Exercise: Algebraic Expression -2 x 3 + 3 x 2 - 40 5 x 2 y - z abd 3 f-1 1 – y + z 2 + π x 2 3 – 24) (c -1 y Variables Constant Term Variable Term Numerical Coefficient Literal Coefficient No. of Terms